大学・一般数学– category –
-

シンプソンの公式(解明編②)
3次以下の関数であればシンプソンの公式が成り立ちます。この記事では、なぜ3次以下でないといけないのかを解明していきます。 Ⅰ シンプソンの公式の誤差 Ⅱ 証明 【】... -

ラグランジュの補間公式
$~n+1~$ 点を通る $~n~$ 次関数を機械的に求めることができるラグランジュの補間公式についてです。 $~n=2~$ のときの事例を中心に紹介します。 Ⅰ ラグランジュの補間... -

シンプソンの公式(解明編①)
シンプソンの公式の右辺で、 $~f(a)~$ と $~\displaystyle f\left( \frac{a+b}{2} \right)~$ と $~f(b)~$ の係数が $~1,4,1~$ になる理由を解明していきます。 Ⅰ シン... -

シンプソンの公式(応用編②)
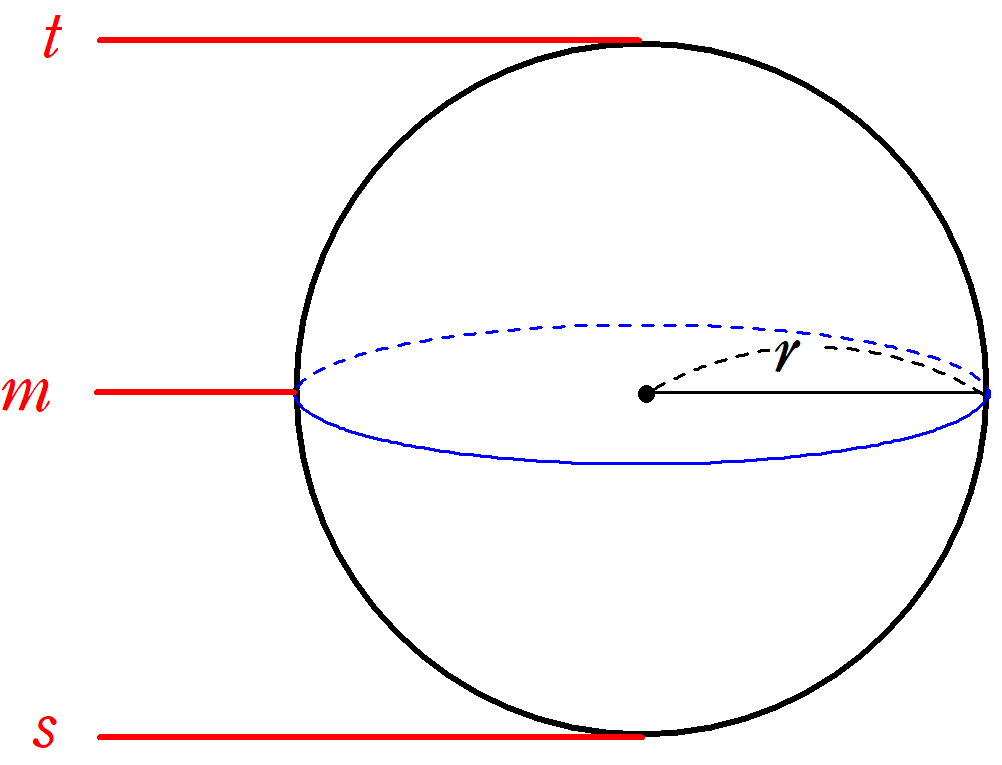
シンプソンの公式は単純な積分のみならず、考え方次第では体積を求めるのにも使えます。 前回に引き続き、その例をいくつか紹介します。 Ⅰ 体積への拡張 Ⅱ 球の体積 Ⅲ... -

シンプソンの公式(応用編①)
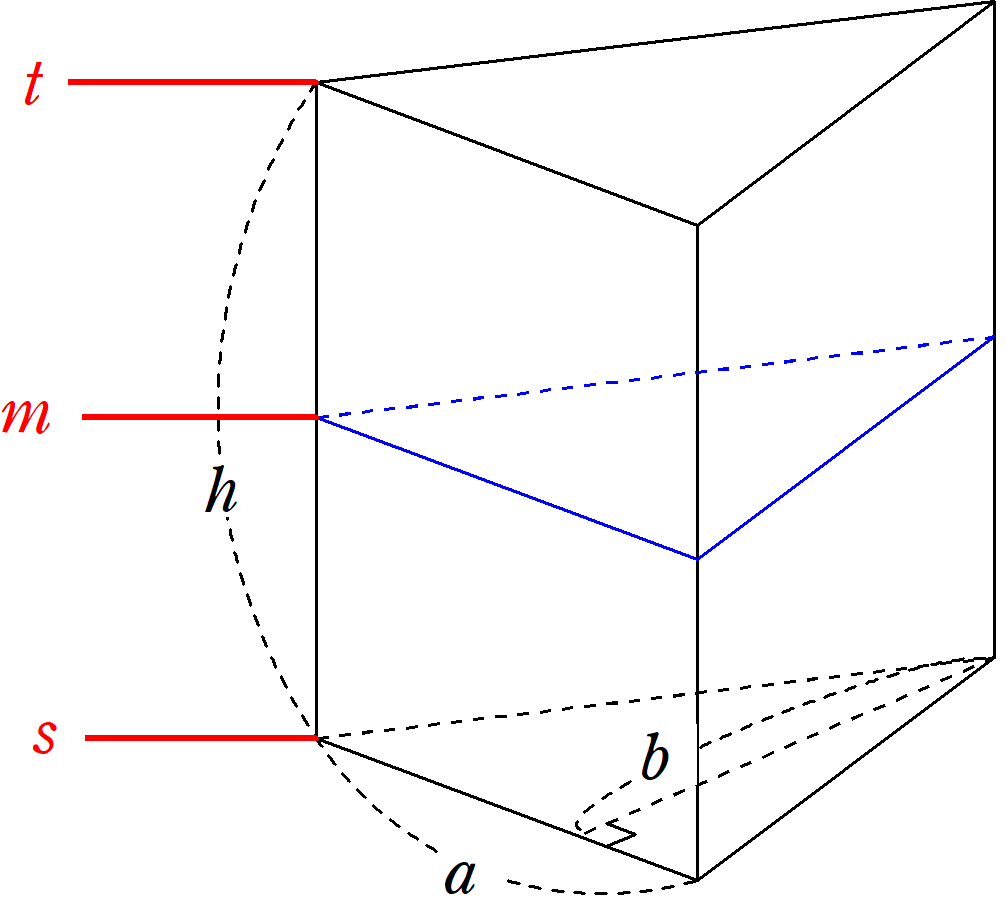
シンプソンの公式は単純な積分のみならず、考え方次第では体積を求めるのにも使えます。 今回はその例をいくつか紹介します。 Ⅰ 体積への拡張 Ⅱ 三角柱の体積 Ⅲ 円錐... -

シンプソンの公式(基本編)
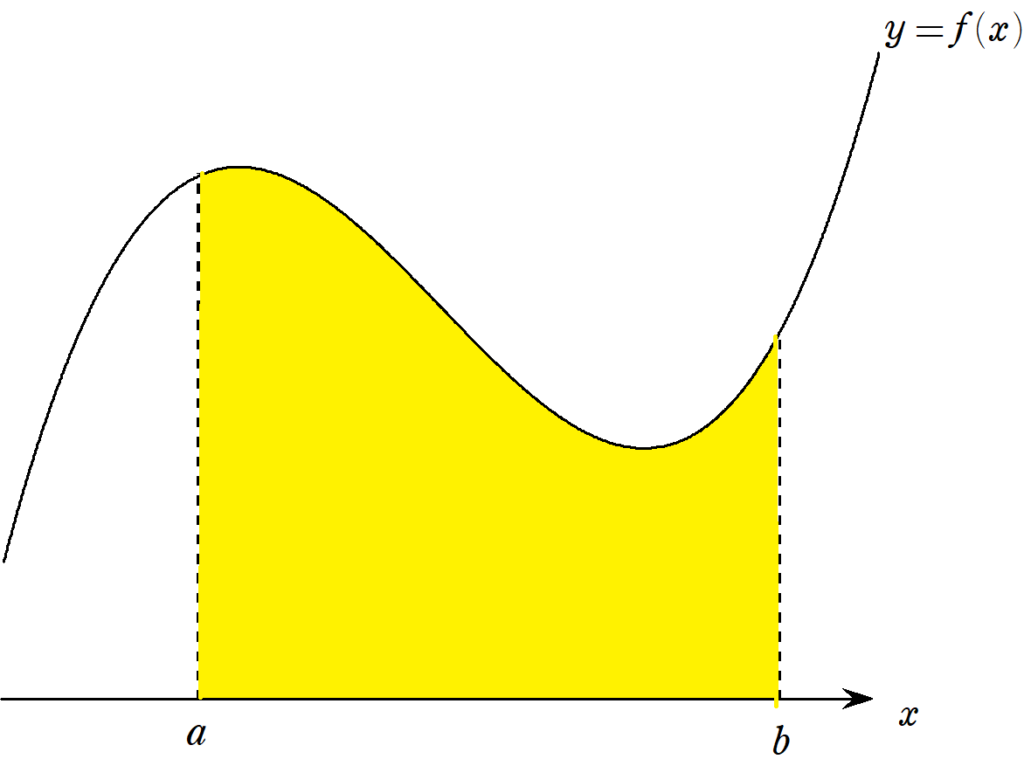
3次以下の関数の積分を求める際に使えるシンプソンの公式。まずは例と簡単な証明を与えます。 Ⅰ シンプソンの公式 Ⅱ 基本例 Ⅲ 反例 Ⅳ 証明1 【】 1743年、イギ... -

メルカトル級数
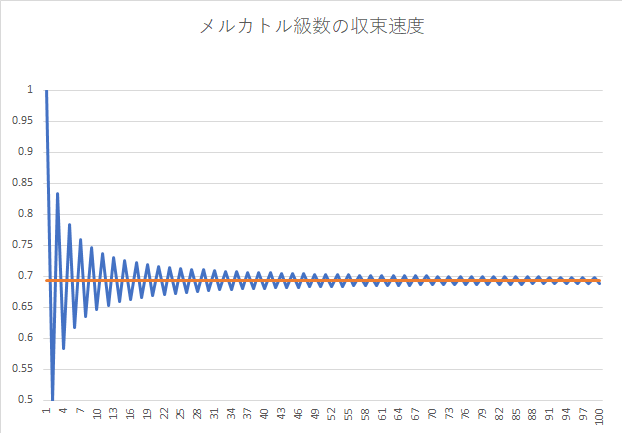
1668年、ニコラウス・メルカトルによって示された級数です。 $~\log{2}~$ の値が単純な分数の足し算・引き算によって表されます。今回もこの級数を使って、近似値計算... -

ロルの定理は当たり前?定理の意味と証明をわかりやすく解説!
平均値の定理を証明する上で必要なロルの定理。数学の定理ではよくあることですが、書いてあることは当たり前のことでも、数式にするとわかりづらい内容となっています。この記事では、ロルの定理の意味を例示で説明するとともに、ロルの定理の証明を解説!ロルの定理が使えないパターンも示してあるため、定理の中身をしっかりと理解できます。 -

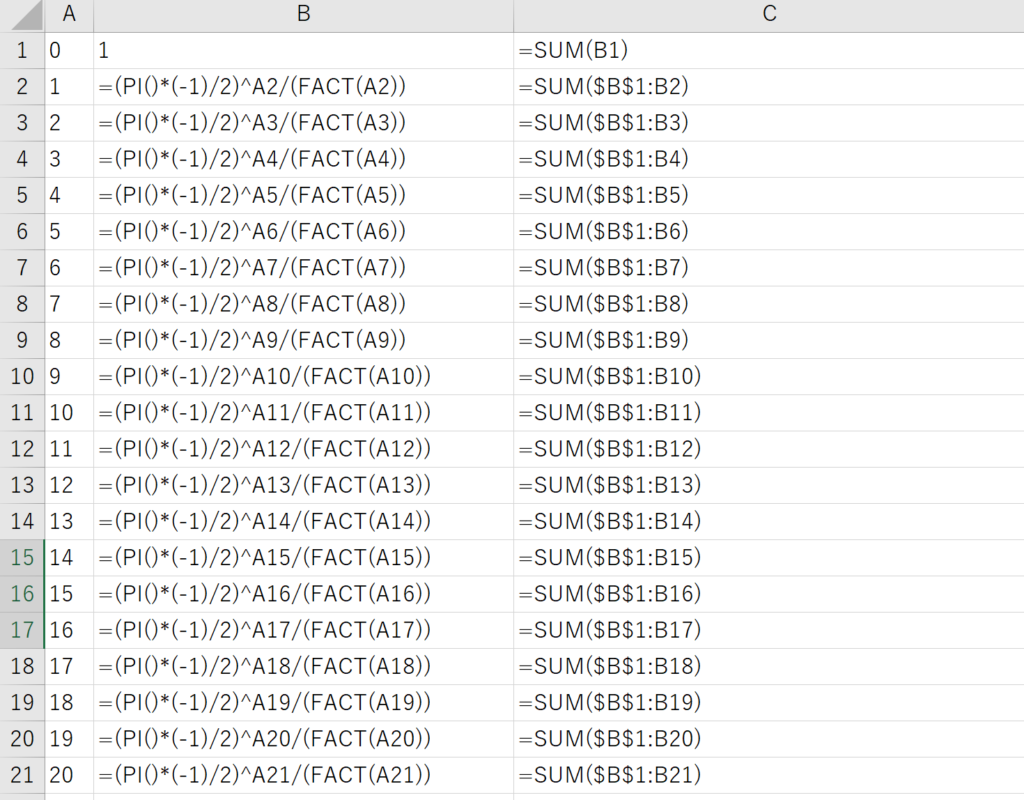
iのi乗
虚数 $~i~$ の $~i~$ 乗はなんと実数になります。実際に $~i^i~$ を計算し、近似値を算出しました。 Ⅰ $~i^i~$ の計算 Ⅱ $~i^i~$ の近似値 【】 $~i~$ の $~i~$ 乗 ... -

複素数の対数関数
対数と言えば $~\log{x}~$ ですが、この定義域を複素数の範囲まで拡張すると、話が単純ではなくなってしまいます。対数関数の表し方とその導き方を紹介します。 Ⅰ 対数...