教科書数学– category –

この記事では、数ある三平方の定理の証明の中でも、トレミーの定理を利用した方法を、現役数学教員が解説します。トレミーというのは２世紀の数学者プトレマイオスのことです。この記事を読んで、トレミーの定理から簡単に三平方の定理を導きましょう。

この記事では、数ある三平方の定理の証明の中でも、芸術家レオナルド・ダ・ヴィンチが考えた方法を、現役数学教員が解説します。証明の出発点の図は、ユークリッドの証明と同じ。その理由についても、ダ・ヴィンチの交友関係から予想されることを論じています。この記事を読んで、ダ・ヴィンチの数学的な才と彼の残した芸術的な証明方法を味わいましょう。

この記事では、数ある三平方の定理の証明の中でも、方べきの定理を利用した方法を２種類、現役数学教員が解説します。また、この証明方法が生まれた時期を探るべく、ユークリッドの『原論』の中の方べきの定理に関する記述も紹介します。

この記事では、数ある三平方の定理の証明の中でも、内接円を利用した方法を現役数学教員が解説します。また、この証明方法の生みの親を巡って、三平方の定理ヲタクのルーミスという人物についても紹介します。この記事を読んで、三平方の定理の証明のバリュエーションを増やしましょう。

3次以下の関数であればシンプソンの公式が成り立ちます。この記事では、なぜ3次以下でないといけないのかを解明していきます。 Ⅰ　シンプソンの公式の誤差 Ⅱ　証明 【】...

$~n+1~$ 点を通る $~n~$ 次関数を機械的に求めることができるラグランジュの補間公式についてです。 $~n=2~$ のときの事例を中心に紹介します。 Ⅰ　ラグランジュの補間...

シンプソンの公式の右辺で、 $~f(a)~$ と $~\displaystyle f\left( \frac{a+b}{2} \right)~$ と $~f(b)~$ の係数が $~1,4,1~$ になる理由を解明していきます。 Ⅰ　シン...

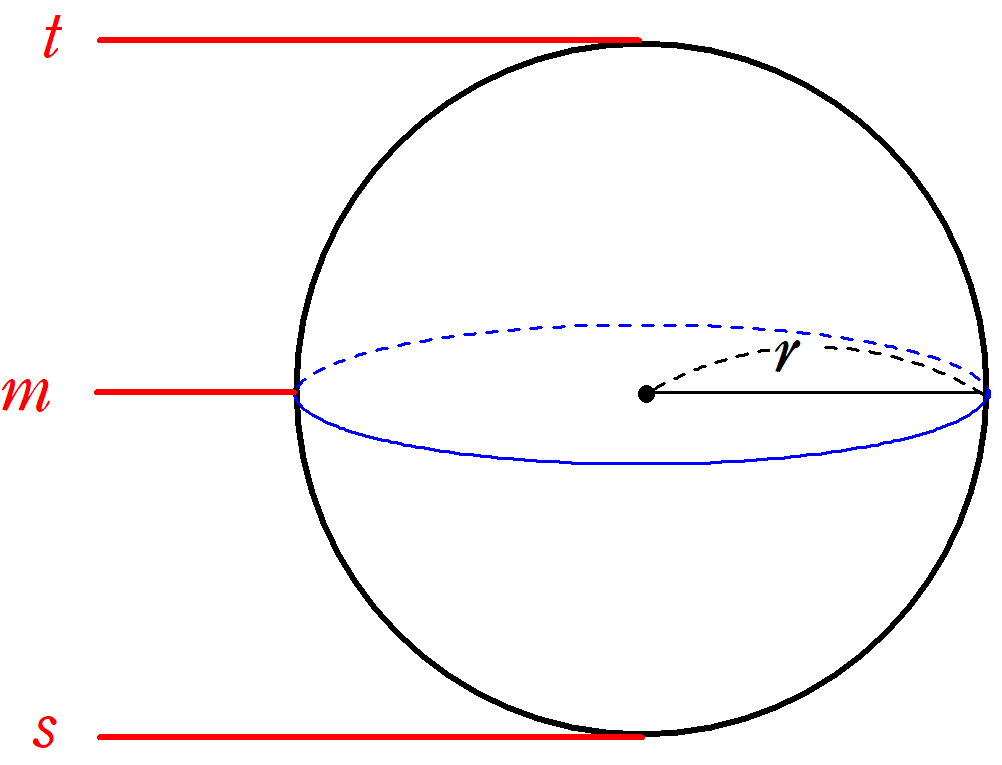
シンプソンの公式は単純な積分のみならず、考え方次第では体積を求めるのにも使えます。 前回に引き続き、その例をいくつか紹介します。 Ⅰ　体積への拡張 Ⅱ　球の体積 Ⅲ...

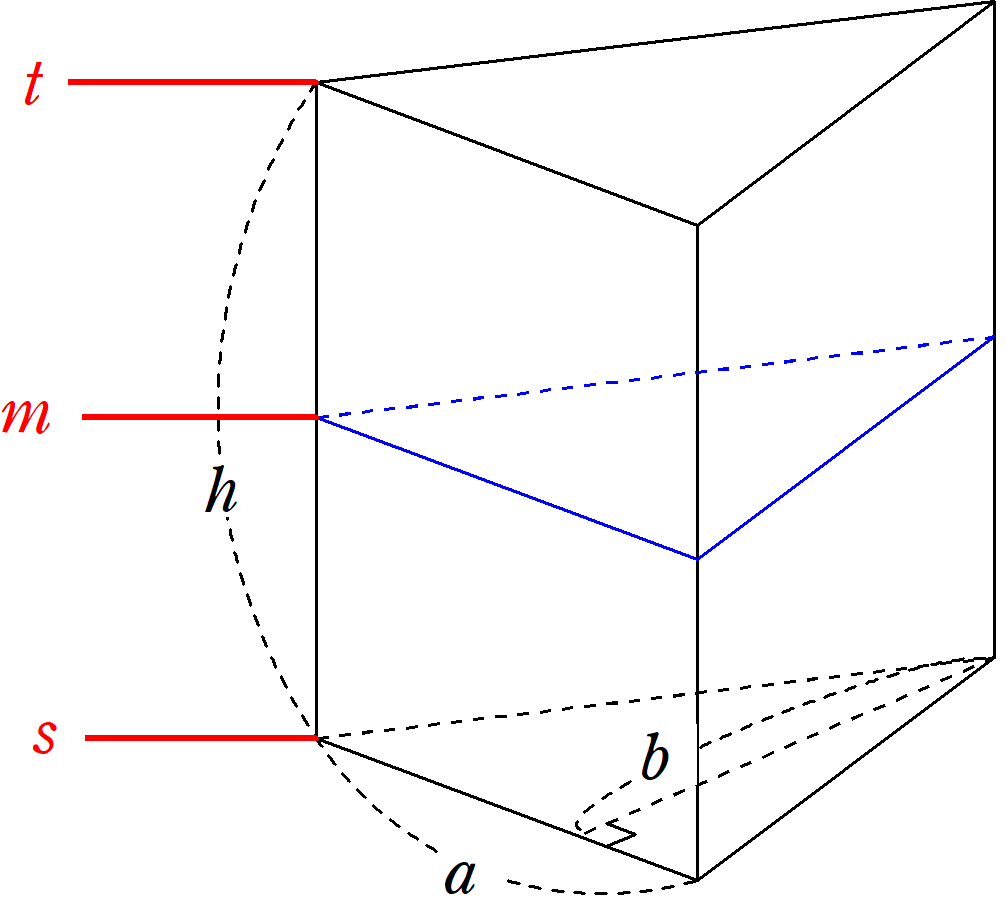
シンプソンの公式は単純な積分のみならず、考え方次第では体積を求めるのにも使えます。 今回はその例をいくつか紹介します。 Ⅰ　体積への拡張 Ⅱ　三角柱の体積 Ⅲ　円錐...

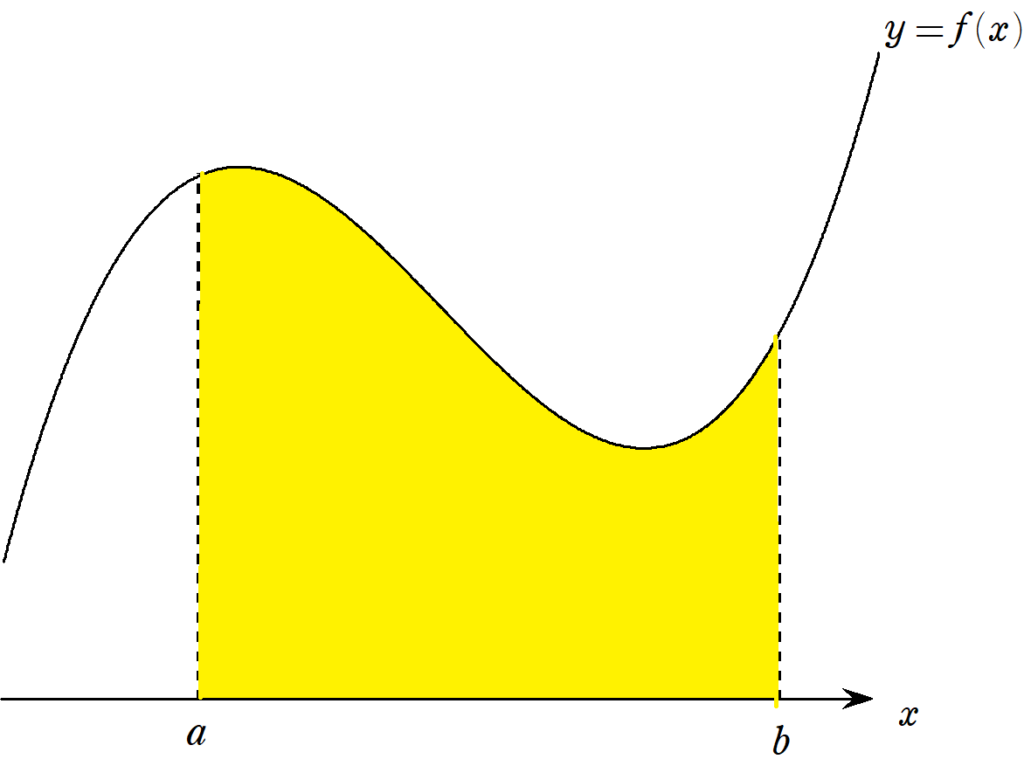
３次以下の関数の積分を求める際に使えるシンプソンの公式。まずは例と簡単な証明を与えます。 Ⅰ　シンプソンの公式 Ⅱ　基本例 Ⅲ　反例 Ⅳ　証明１ 【】 　1743年、イギ...