【数学史３－３】バビロニアでは小数まで60進法！その利点と問題点は？

2021年2月7日2023年12月16日

当ページのリンクには広告が含まれています。

　60進法で有名なバビロニア（メソポタミア）。

　楔型文字で用意された$~10~$と$~1~$だけで、大きな数だけでなく、小数まで表すことができました。

　しかし、隣接していた古代エジプトの10進法と比べると、数値としては非常にわかりづらいものとなっています。

　それでもバビロニアが60進法を採用し続けた理由は、$~60~$という数の特殊性とメソポタミアの長い歴史にありました。

　この記事では、バビロニアの小数の問題点にも触れつつ、その表し方や60進法の利点について解説します。

この記事を読んでわかること

バビロニアの小数の表し方とその問題点
バビロニアで60進法が採用され続けた理由

この記事で主に扱っている時代と場所

時代	B.C.1750年頃
場所	バビロニア（メソポタミア）

この記事を読んでわかること

バビロニアの小数の表し方

　同時期の古代エジプトでは、$~1~$より小さい数を表すにあたって、単位分数を用いていました。

小数第一位は 60分の1 の位

　まず、現在我々が使っている$~10~$進法の小数を分析すると、

小数第一位$~\left(\displaystyle \frac{1}{10}=10^{-1}~の位 \right)~$
小数第二位$~\left(\displaystyle \frac{1}{100}=10^{-2}~の位 \right)~$
小数第三位$~\left(\displaystyle \frac{1}{1000}=10^{-3}~の位 \right)~$

と続いていきます。

　そのため、$~0.325~$という小数を例にとると、

0.325=\frac{1}{10}\times 3+\frac{1}{100}\times 2+\frac{1}{1000}\times 5

のように数が成り立っています。

　バビロニアで使われていた$~60~$進法の小数を同じように考えると、

小数第一位$~\left(\displaystyle \frac{1}{60}=60^{-1}~の位 \right)~$
小数第二位$~\left(\displaystyle \frac{1}{3600}=60^{-2}~の位 \right)~$
小数第三位$~\left(\displaystyle \frac{1}{216000}=60^{-3}~の位 \right)~$

と続いていきます。

　楔形文字で表される数字は、整数と同様に2種類のみ。
　図1のように、小数が表されました。　

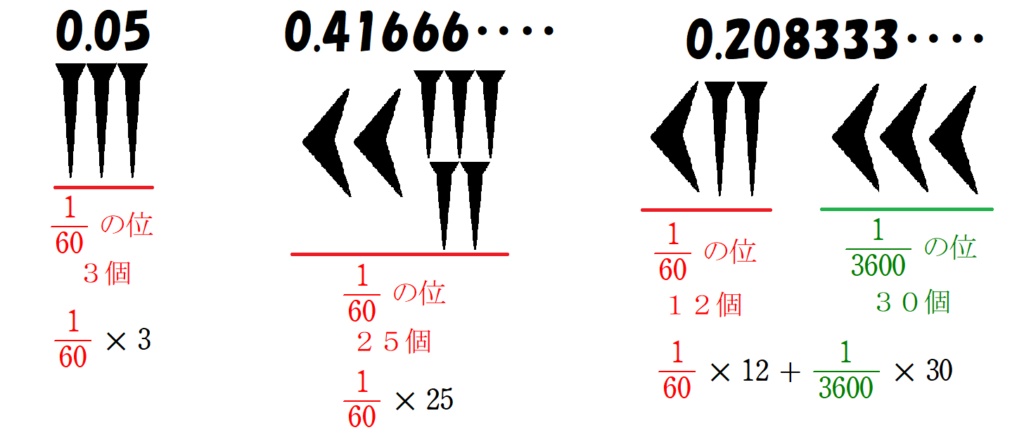
小数点は存在しなかった

　バビロニアの小数には小数点が存在せず、どこまでが整数で、どこからが小数なのかが判別しづらいものでした。

　また、「$~0~$」も存在しなかったため、粘土板に刻まれた数字がどこの位に属するものなのかは、非常にわかりづらいものとなっています。

　例として、図2の「1 1」を考えてみます。

　この2つの数字を整数のみで解釈するなら、以下のような候補が上がります。

$~60~$の位が１個、$~1~$の位が１個で、$~60 \times 1+1\times 1=61~$
$~3600~$の位が１個、$~1~$の位が１個で、$~3600 \times 1+1\times 1=3601~$（$~60~$の位は空所）
$~3600~$の位が１個、$~60~$の位が１個で、$~3600 \times 1+60\times 1=3660~$（$~1~$の位は空所）

　しかし、小数部分も含めて解釈するとなると、

$~1~$の位が１個、$~\displaystyle \frac{1}{60}~$の位が１個なら、$~\displaystyle 1 \times 1+\frac{1}{60}\times 1=1.0166\cdots~$
$~1~$の位が１個、$~\displaystyle \frac{1}{3600}~$の位が１個なら、$~\displaystyle 1 \times 1+\frac{1}{3600}\times 1=1.00027\cdots~$$~\left( \displaystyle \frac{1}{60}~の位は空所 \right)~$
$~\displaystyle \frac{1}{60}~$の位の位が１個、$~\displaystyle \frac{1}{3600}~$の位が１個なら、$~\displaystyle \frac{1}{60} \times 1+\frac{1}{3600}\times 1=0.0169\cdots~$（$~1~$の位は空所）

など、より多様な読み方ができてしまうのです。

数の位は文脈から判断していた

　小数点も$~0~$も存在しなかったため、数字の位は文脈から判断するしかありませんでした。

　一の位、十の位、‥‥といった整数部分だけならともかく、小数第一位、小数第二位、‥‥といった小数部分まで判断の候補に入れると、「1」という数字だけでも様々な解釈ができてしまいます。

　次の例を見てみましょう。

「1」を使った文章の例

(1)　おじいちゃんは$~60~$歳だ。
　年齢なので整数となるが、おじいちゃんなので1歳はあり得ず、3600歳は生きられない。

(2)　昼食にパンを$~1~$個食べた。
　パンの個数なので整数となるが、60個や3600個もパンを食べる人はそういないはず。

(3)　視力が$~\displaystyle \frac{1}{60}=0.016 \cdots~$しかないので、眼鏡が必要だ。
　視力なので$~0.01~$から$~2.0~$の間になるが、$~1~$なら眼鏡は必要ないはず。

(4)　バチカン市国の人口は、茨城県の人口の$~\displaystyle \frac{1}{3600}=0.00027 \cdots~$ほどだ。
　バチカン市国の人口は615人（外務省、2018年10月）であり、茨城県の人口は約285万人（茨城県、2020年12月）なので、$~615 \div 2850000=0.00022 \cdots~$。

　このように、文脈から判断するためには、読解力や推測力、知識が必要となりそうです。

バビロニアで60進法が使われた理由

　近隣のエジプトが10進法を採用していたのに対し、バビロニア人はなぜ60進法を採用したのでしょうか？

　$~60~$という数の性質と歴史の両面から、その理由を推測します。

60は約数が多い

　$~10~$や$~100~$に比べ、優れているのは約数の多さ。

$~10~$の約数‥‥$~1,2,5,10~$
$~100~$の約数‥‥$~1,2,4,5,10,20,25,50,100~$
$~60~$の約数‥‥$~1,2,3,4,5,6,10,12,15,20,30,60~$

　$~100~$よりも約数を多く持つため、さまざまな数で割ることができるという利点があります。

　特に、片手の指の本数である$~5~$までの整数をすべて割ることができるという点で、$~60~$という数が優れていました。

　同じく$~12~$個の約数を持つ2桁の整数$~72~,~90~,~96~$ではなく、$~60~$が優遇された理由は人間の手に関係していたからです。

　約30万年前頃から、指を使って数を数えていたため、数と手の関係はどの場所でも共通でした。

シュメール人は60まで指で数えた

　バビロニアが成立するよりもさらに昔、紀元前2700年頃にはシュメール人の都市国家がこの地に形成されました。

　シュメール人の子供は、$~60~$までの数を指で数える方法を習ったとされています。

シュメール人の指による数え方

左手で$~1~$から$~5~$を数える。
右手の親指が$~6~$を表し、左手はリセット。
右手の親指（$~6~$）を維持したまま、左手で$~7~から$~11~$まで数える。
右手の人差し指が$~12~$を表し、左手はリセット。

　以上を繰り返すことで、右手の小指（$~30~$）まで数える。

　$~31~$以上は、左手と右手を入れ替えて同じように数える。

　実際の様子を図にすると、以下のようになります。

　この数え方であれば、理論上$~71~$まで数えることができます。

　そのため、$~60~$で数えるのを止めていることは、バビロニアで数体系が確立する遥か昔から、この地で$~60~$進法が使われてきた証拠にもなっています。

まとめ・参考文献

　　バビロニアにおける小数の表し方や、$~60~$進法が好まれた理由について解説してきました。

小数第一位は$~\displaystyle \frac{1}{60}~$の位。
小数点が無いため、数の位は文脈から判断した。
$~60~$進法採用の理由は、$~60~$の約数の多さ。

　$~60~$進法における四則計算の方法について、次の記事で解説します。

次の記事へ

【数学史３－４】バビロニアの計算方法は？表を見るだけでかけ算とわり算ができる！ 60進法が使われたバビロニアにおいて、かけ算やわり算は「数表」という道具を使って計算しています。かけ算では「積表」を使って調べるだけ、わり算では「逆数表」と「積表」を併用することで答えを出していました。この記事では、その数表の中身や使い方を解説。当時のバビロニア人がわり算で計算ミスをしまくっていた理由もわかります。

この章のまとめへ

【数学史まとめ３】バビロニアの数学　メソポタミアの数学のことを、数学史上では「バビロニアの数学」と言い表します。紀元前1750年頃に数体系が確立していたバビロニア。実生活で使う範囲を超えた数学の記録が粘土板に今も残っています。この記事では、バビロニアの数学に関する事柄を年表形式でまとめると共に、バビロニアが紀元前に誇った高度な数学を大まかに解説します。