【数学史３－８】バビロニアでは平方根の研究も？粘土板に残された√2の値とは？

　二次方程式や三平方の定理の研究が進んでいたバビロニア。

　これらを考える上で避けて通れないのが、平方根の考え方です。

　実はバビロニアでは、$~\sqrt{2}~$の近似値を小数第5位まで正確に割り出していました。

　そのことが残っている粘土板や、相加相乗平均を利用した平方根の求め方について、この記事では解説します。

当ブログ管理人Fukusukeの2冊目の著書が6月11日に発売！
数学史×世界史の新感覚ノンフィクション！

Amazonで『教養としての数学史』を見る

楽天市場で『教養としての数学史』を見る

正方形の対角線を求めた粘土板

　二次方程式や三平方の定理を考える上で不可避なのが平方根の考え方。

　それらの問題を解く上では、バビロニアお得意の数表（平方根表）が使われましたが、バビロニア人は平方根の値を細かく計算する術を持っていました。

YBC7289に残る30√2

　平方根の値を、どのくらい細かく知っていたかがわかる資料が、粘土板（YBC:Yale Babylonian Collection）7289 です。

　この粘土板には、楔形文字で図2のような正方形が刻まれていました。（60進法の表記で、「;」は小数点、「,」は位の境目を表しています。）

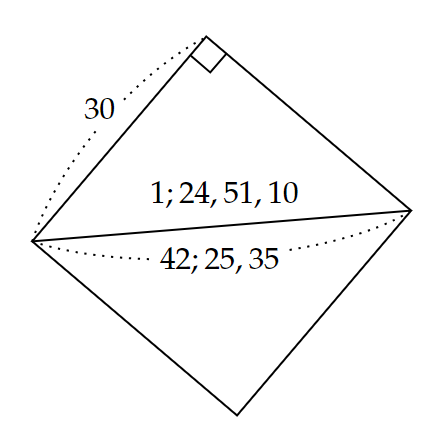
　　これを現在の10進法表記に直すと、図3のようになります。

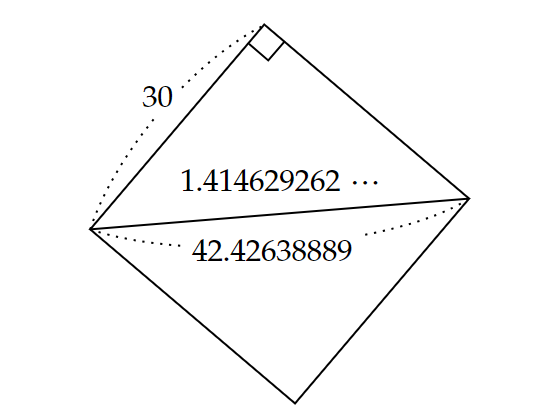
　この図から、１辺$~30~$の正方形の対角線の長さを、

30 \times 1.41421296\cdots=42.42638889 \cdots

と計算していたことがわかります。

√2の値の誤差は0.0000006

　　現在わかっている知識では、

\sqrt{2}=1.41421356\cdots

なので、バビロニアで求められた$~\sqrt{2}~$の近似値の誤差は、

|1.41421296-1.41421356|=0.0000006

です。

　非常に精度の高い近似が、バビロニアで行われていたことがわかります。

√2の近似値の算出方法

　通常であれば、以下のような計算で$~\sqrt{2}~$の近似値を細かく算出することができます。

\begin{align*}
1&< \sqrt{2} < 2  \\
1.4=\sqrt{1.96} &< \sqrt{2} < \sqrt{2.25}=1.5\\
1.41=\sqrt{1.9881} &< \sqrt{2} < \sqrt{2.0164}=1.42\\
&~~~~~~~~\vdots
\end{align*}

　しかし、積表のケタ数に限りがあり、筆算という技術もないバビロニアでは、別の方法で$~\sqrt{2}~$の近似値を求めました。

相加相乗平均による√2の近似値の求め方

　バビロニアで平方根の近似値を求めるために使われたのは、今で言う相加相乗平均の考え方です。

\frac{2}{a_1} < \sqrt{2} < a_1 

a_2=\frac{1}{2}\left(a_1+\frac{2}{a_1} \right)=\frac{1}{2}\left( \frac{3}{2}+\frac{4}{3} \right)=\frac{17}{12}

\begin{align*}a_3&=\frac{1}{2}\left(a_2+\frac{2}{a_2} \right) \\
\\a_4&=\frac{1}{2}\left(a_3+\frac{2}{a_3} \right) \\
&~~~~~~~~~~~\vdots
\end{align*}

　上記の方法の中で、数学的論証が必要な部分（※１～※３）については、以下のように補足しておきます。

\begin{align*}a_1-a_2&=a_1-\frac{1}{2}\left(a_1+\frac{2}{a_1} \right) \\
\\&=\frac{1}{2}a_1-\frac{1}{a_1} \\
\\
&=\frac{1}{a_1} \left( \frac{1}{2}a_1^2-1 \right) \\\end{align*}

a_2=\frac{1}{2}\left(a_1+\frac{2}{a_1} \right) \ge \sqrt{a_1 \cdot \frac{2}{a_1}}=\sqrt{2}

　ちなみに、※３の結果からわかるように、$~\sqrt{3}~$の近似値を求めたい場合には、

a_{n+1}=\frac{1}{2}\left(a_n+\frac{3}{a_n} \right)

の計算をしていけばよいことになります。

実際に√2を近似してみた

　実際に、$~\sqrt{2}~$の近似値をバビロニアの方法で求めてみましょう。

a_{n+1}=\frac{1}{2}\left(a_n+\frac{2}{a_n} \right)

a_2=\frac{1}{2}\left(a_1+\frac{2}{a_1} \right)=\frac{1}{2}\left( \frac{3}{2}+\frac{4}{3} \right)=\frac{17}{12}

a_3=\frac{1}{2}\left(a_2+\frac{2}{a_2} \right)=\frac{1}{2}\left( \frac{17}{12}+\frac{24}{17} \right)=\frac{577}{408}

a_4=\frac{1}{2}\left(a_3+\frac{2}{a_3} \right)=\frac{1}{2}\left( \frac{577}{408}+\frac{816}{507} \right)=\frac{665857}{470832}

　初期値($~a_1~$)によって、必要な計算回数は変わるものの、少ない回数で$~\sqrt{2}~$の近似値を計算することができました。

　ここで求めた$~\displaystyle \frac{665857}{470832}~$は、$~\sqrt{2}~$の実値と小数第11位まで一致しています。

実際に√3を近似してみた

　ついでに、$~\sqrt{3}~$についても近似してみます。

a_{n+1}=\frac{1}{2}\left(a_n+\frac{3}{a_n} \right)

a_2=\frac{1}{2}\left(a_1+\frac{3}{a_1} \right)=\frac{1}{2}\left( \frac{9}{5}+\frac{5}{3} \right)=\frac{26}{15}

a_3=\frac{1}{2}\left(a_2+\frac{3}{a_2} \right)=\frac{1}{2}\left( \frac{26}{15}+\frac{45}{26} \right)=\frac{1351}{780}

a_4=\frac{1}{2}\left(a_3+\frac{2}{a_3} \right)=\frac{1}{2}\left( \frac{1351}{780}+\frac{2340}{1351} \right)=\frac{3650401}{2107560}

　ここで求めた$~\displaystyle \frac{3650401}{2107560}~$は、$~\sqrt{3}~$の実値と小数第12位まで一致しています。

　様々な数について、この計算式を応用することで、バビロニアでは「平方根表」が完成しました。

　教科書の巻末に載っている平方根表の元祖とも言えるでしょう。

まとめ・参考文献

　バビロニアにおける平方根の近似式について解説してきました。　

• バビロニアの$~\sqrt{2}~$の近似値は、小数第5位まで一致していた。
• 相加相乗平均の考え方を応用し、近似値を細かく計算する術を知っていた。

　証明という概念が無かったため、近似式の裏付けまではしなかったものの、平方根を細かく計算するためのアルゴリズムを知っていた点で、バビロニア代数のレベルの高さが窺えるでしょう。

　次の記事からは、紀元前のインドにおける数学について解説します。

次の記事へ

【数学史４－１】インド数学も古代では未発展？その歴史とブラーフミー数字について解説！ 数学と言えばインドですが、紀元前におけるインドは同じ四大文明のエジプト、メソポタミア、中国と比べて数学的な面で劣っていました。その理由を古代インドの歴史から考察すると共に、現代のアラビア数字につながる、古代インドの偉大な発明「ブラーフミー数字」の表し方を解説します。

この章のまとめへ

【数学史まとめ３】バビロニアの数学 　メソポタミアの数学のことを、数学史上では「バビロニアの数学」と言い表します。紀元前1750年頃に数体系が確立していたバビロニア。実生活で使う範囲を超えた数学の記録が粘土板に今も残っています。この記事では、バビロニアの数学に関する事柄を年表形式でまとめると共に、バビロニアが紀元前に誇った高度な数学を大まかに解説します。

高度過ぎてついていけない・・・。

紀元前とは思えないよね。