【数学史５－６】平方根は有限のみ対応！『九章算術』の開平法とは？

　紀元前に誕生し、中国数学の体系を完成させた『九章算術』。

　『九章算術』の4章「少広」では、面積がわかっている正方形の一辺の長さを求める問題が載っていました。

　この記事では、古代中国の開平法について解説。

　有限値でないと扱えなかったものの、面積を分割する巧みな方法で平方根の値を求めています。

『九章算術』4章「少広」

　『九章算術』は紀元前2世紀頃に書かれ、その後の中国数学を体系立てた数学書です。

　全9章の中の4章は「少広」で、第1章の「方田」の逆、すなわち面積や体積から一辺の長さを求める問題が載っていました。

前半は小学校レベルの難易度

　『九章算術』4章の第1問～第11問はすべて、横の長さがわかっている面積$~1~$畝^※1の長方形で、縦の長さを求める問題でした。

※1「畝」は現在でも使われている面積の単位で、1畝＝240平方歩。

　そのため、現代数学ならば単なるわり算で求められるということになります。

　実際に4章の最初の問題を見てみましょう。

　現代数学であれば、

\begin{align*}
&~~~240 \div 1~\frac{1}{2}  \\
\\
&=240 \div \frac{3}{2}  \\
\\
&=240 \times \frac{2}{3}  \\
\\
&=160~~(歩)
\end{align*}

と単なるわり算だけで求められます。

　しかし、古代中国での計算はそう単純なものではありませんでした。

単位分数の和を割る方法

　『九章算術』4章第1問は、以下の方法で解かれました。

1\times2+\frac{1}{2}\times2=3

240 \times2 \div3=160

　この考え方を現代数学で捉えると、

\frac{240}{1+\frac{1}{2}}=\frac{240 \times 2}{1 \times 2+\frac{1}{2} \times 2}=\frac{240 \times 2}{3}

であり、通分の手間を減らすための考え方であったとも考えられています。

　『九章算術』の4章第2問以降も、面積$~1~$畝で廣（横）が単位分数の和で表されている田の縦を求める問題が続き、第11問では

240 \div \left( 1+\frac{1}{2}+\frac{1}{3}+\cdots+\frac{1}{12} \right)

を計算するところまで計算量が増えています。

　古代中国の、実生活に即した単位分数へのこだわりや、算木による計算力の高さがわかる問題群と言えるでしょう。

平方根の求め方

　『九章算術』の4章「少広」は、わり算で求められる前半部分に対し、後半部分は平方根や立方根の考え方を要する問題が続きます。

正方形の面積から一辺を求める問題

　『九章算術』4章の第1問から第11問までは、面積と横の長さが分かっている長方形から、縦の長さを求める問題が並んでいました。

　しかし、第12問から正方形に関する問題へと変わります。

　正方形の一辺を$~x~$歩とすれば、

x^2=55225

となり、まさに$~55225~$の正の平方根を求める問題となっています。

正方形を使った開平法

　『九章算術』の中で、開平法は「開平術」と呼ばれ、平方根を求めるための算木の動かし方を説明していました。

　そこに載っている算木の動かし方から推測される、平方根を求めるための考え方を理解してみましょう。

『九章算術』4章第12問の解説

　正方形の一辺の長さについて、その百の位を$~a~$、十の位を$~b~$、一の位を$~c~$とし、

(100a+10b+c)^2=55225

を満たす$~a~,~b~,~c~$を求める。

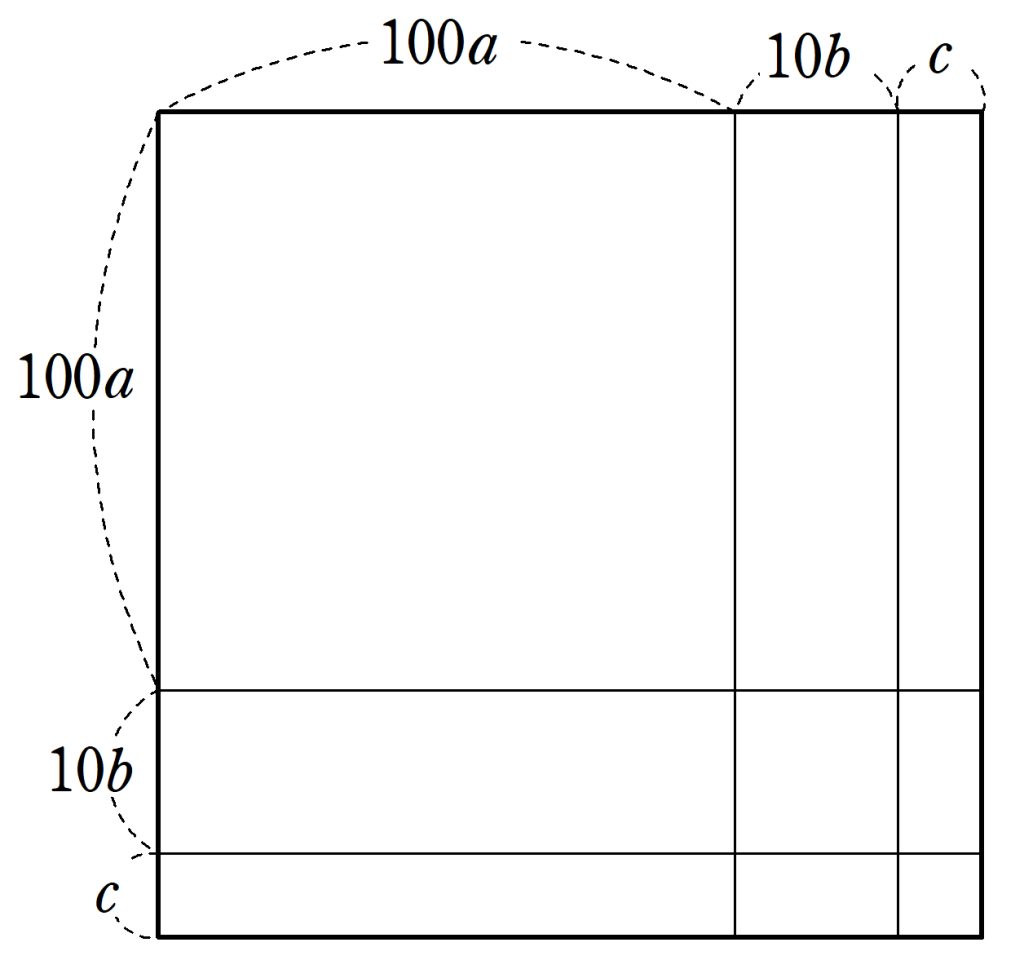
　最上位桁の$~a~$は、

\begin{align*}
(100a)^2 &< 55225 \\
 10000a^2 &<55225 
\end{align*}

より、$~a=2~$と求まる。

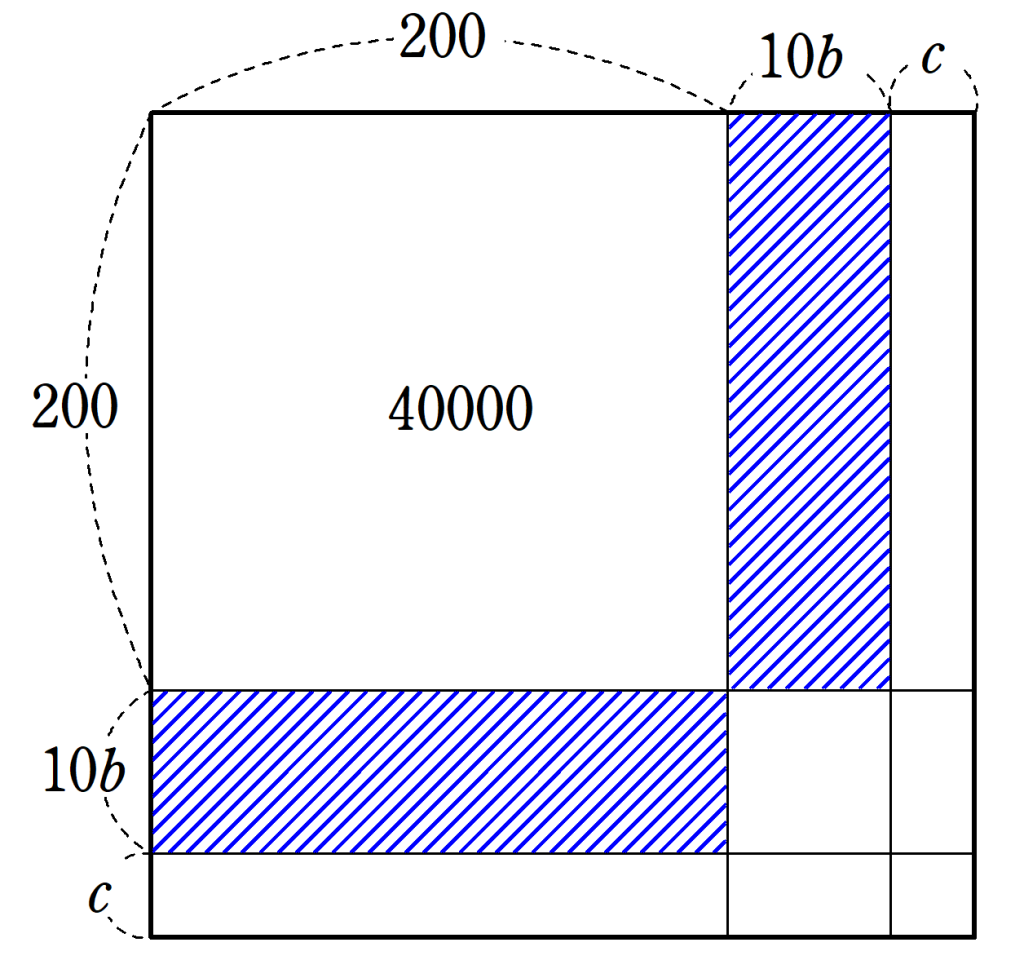
　次に、図4の斜線部の和は、

2 \times 200 \times 10b=4000b

であり、これが$~55225-40000=15225~$より小さいので、

4000b < 15225 

より、$~b=3~$が候補となる。

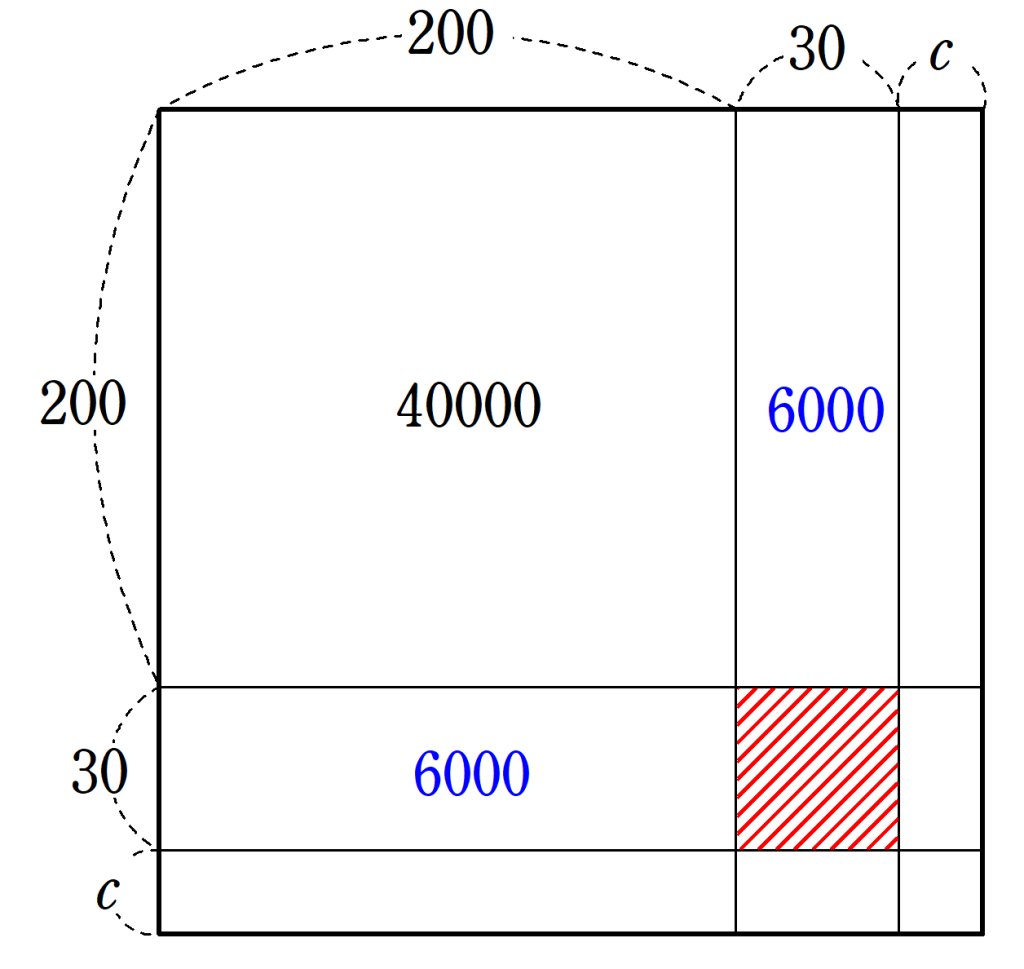
　ここで、図5の斜線部をたしても、$~55225~$以下であることを確かめる必要がある。

40000+6000+6000+900=52900 < 55225 

より、図5の条件を満たしているため、$~b=3~$が確定した。

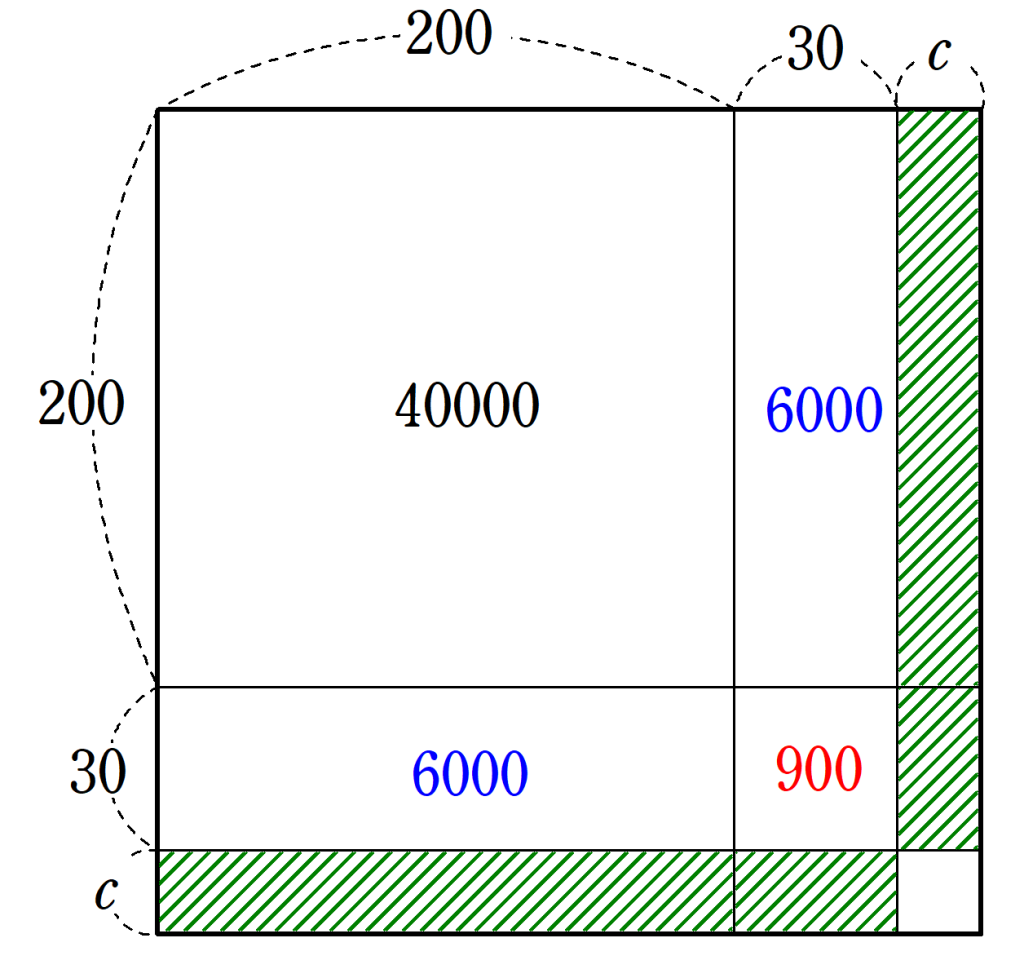
　$~c~$についても同様に、図6の斜線部の和の$~460c~$が、$~55225-52900=2325~$より小さいので、

460c < 2325

より、$~c=5~$が候補となる。

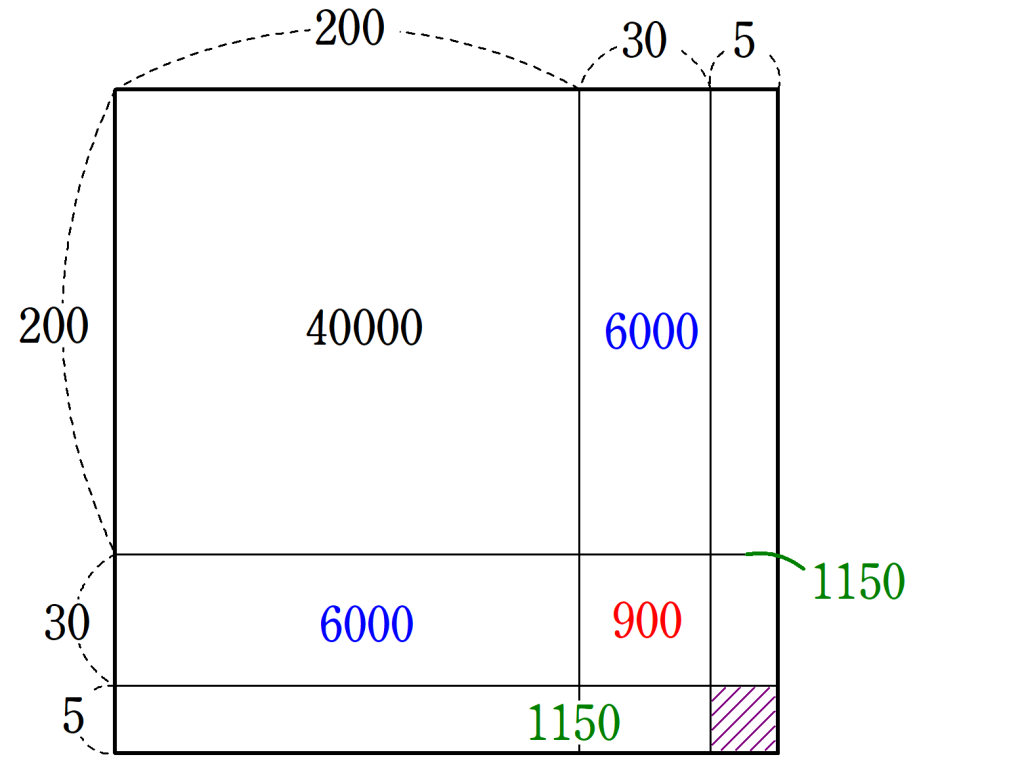
　図7の斜線部をたしても、$~55225~$以下であることを確かめると、

52900+1150+1150+25=55225

であり、与えられた面積と一致したため、この正方形の一辺の長さは$~235~$と求まった。

　このように位を細かくしていき、もとの正方形の面積と一致したら開平術は終了となります。

　そのため、バビロニアの開平法と異なり、$~\sqrt{2}~$のような無理数を求めることはできませんでした。

開平法の応用

　『九章算術』4章第12問以降は、開平法関連の問題が以下のように続きます。

• 第12問～第16問：正方形の面積から一辺の長さを求める問題
• 第17問～第18問：円の面積から円周の長さを求める問題
• 第19問～第22問：立方体の体積から一辺の長さを求める問題
• 第23問～第24問：球の体積から直径を求める問題

　第16問までの開平法を応用した、残りの3種類の問題についても簡単に紹介します。　

円の面積から円周を求める問題

　『九章算術』4章第17問～第18問は、円の面積から円周の長さを求める問題で、以下のように出題されました。　

　『九章算術』1章に、円の面積の公式が4種類載っていて、その中の1つである

(円の面積)=\frac{(円周)^2}{12}

を利用することで、

(円周)^2=12 \times 300=3600

となり、$~3600~$に開平術を使って、円周を$~60~$歩 と求めました。

あわせて読みたい

【数学史５－５】『九章算術』での円周率は3?　実用的な観点で円や弓形を研究していた！ 　紀元前2世紀頃にでき、中国数学を体系立てた数学書である『九章算術』。その1章は、様々な形の田の面積を求める問題が載っており、その中には円や弓形の田も扱われていました。この記事では、それらの問題からわかる円周率の値や、円や弓形の面積の公式について解説します。

立方体の体積から一辺を求める問題

　『九章算術』4章第19問～第22問は、立方体の体積から一辺の長さ求める問題で、以下のように出題されました。　

　これまでの平方根を求める問題と異なり、こちらは立方根を求める問題となっています。

　しかし、図8のような立方体を使い、開平術と同じ要領で解くことができました。

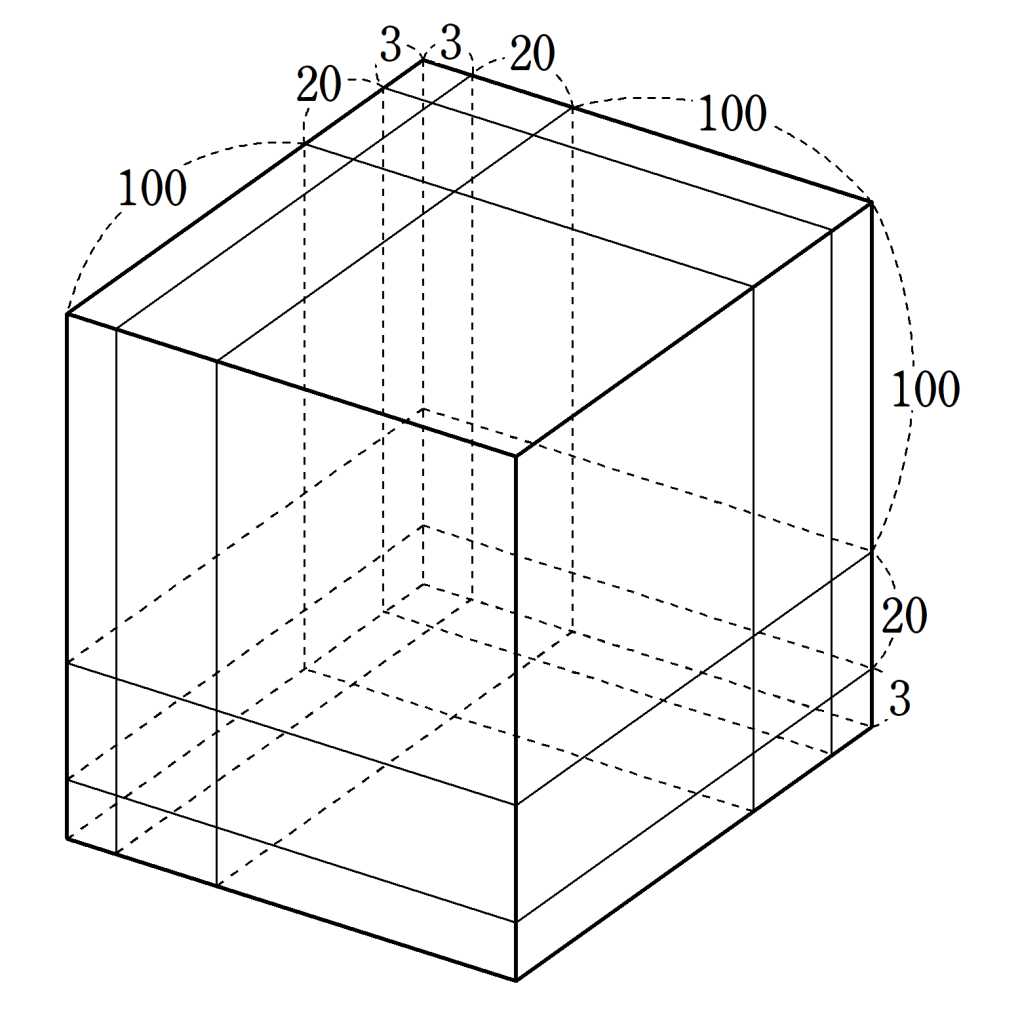
　これにより、一辺の長さを$~123~$尺 と求めています。

球の体積から直径を求める問題

　『九章算術』4章の最後を飾る第23問～第24問は、球の体積から球の直径を求める問題でした。　

　この問題の後に、球の体積の公式が以下のように載っていました。

(球の体積)=\frac{9}{16} \times (直径)^3

　この公式を利用することで、

(直径)^3=\frac{16}{9} \times 4500=8000

となり、$~8000~$の立方根を求め、球の直径を$~20~$尺と求めました。

　ちなみに、ここで使われた球の体積の公式を、$~\pi=3~$として表すと、

V=\frac{3}{2} \pi r^3

であり、$~\displaystyle V=\frac{4}{3}\pi r^3~$と大差ない公式であるとわかります。

まとめ・参考文献

　古代中国における平方根の考え方について解説しました。

• 古代中国の数学書『九章算術』では、幾何的に平方根を求めた。
• 平方根だけでなく、立方根まで幾何的に求めることができた。

　算木という優れた計算道具を持つ紀元前の中国だからこそ、回数の多い計算作業を乗り越えて平方根や立方根を求めることができたのでしょう。

　次の記事では、古代中国の三平方の定理について解説します。

次の記事へ

【数学史５－２】甲骨文字で数字はどう表す？現在の漢数字ができるまでの流れまで解説！ 紀元前16世紀頃の殷時代に使われた甲骨文字。数字も用意されており、基本の13種類の数字とそれらを組み合わせた合字によって、様々な数を表していました。この記事では、その数の表し方を解説すると共に、どのような流れで現在の漢数字（楷書体）へと文字が変化していったのかを辿ります。

この章のまとめへ

【数学史まとめ５】古代中国の数学 　四大文明の一つで長い歴史を持つ中国。 　しかし、紀元前213年の焚書政策により、紀元前の数学関係の資料はほとんど失われてしまいました。 　そのため、古代中国の数…

　素因数分解がない時代だと、ここまで計算が大変なのか・・。

　でも、この方法なら小数や分数で表された数でも根を求めることができるんだ。
　実際、分数の平方根や立方根だって登場していたよ。