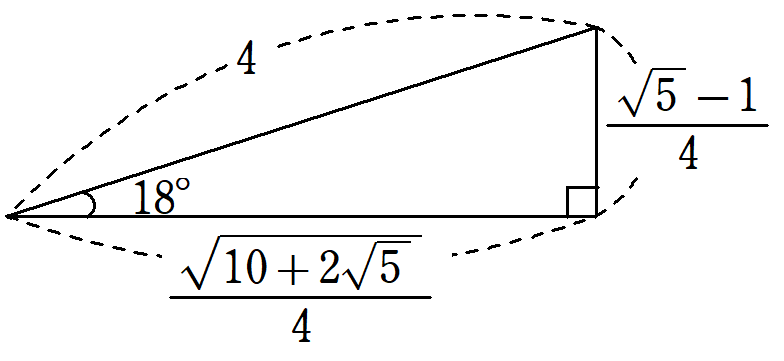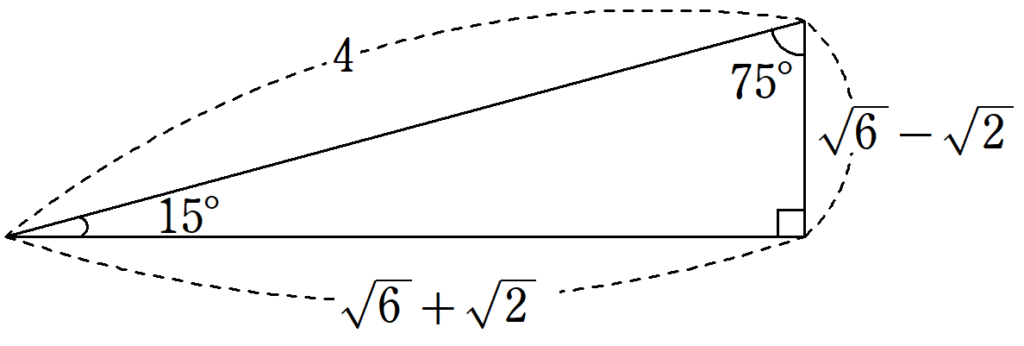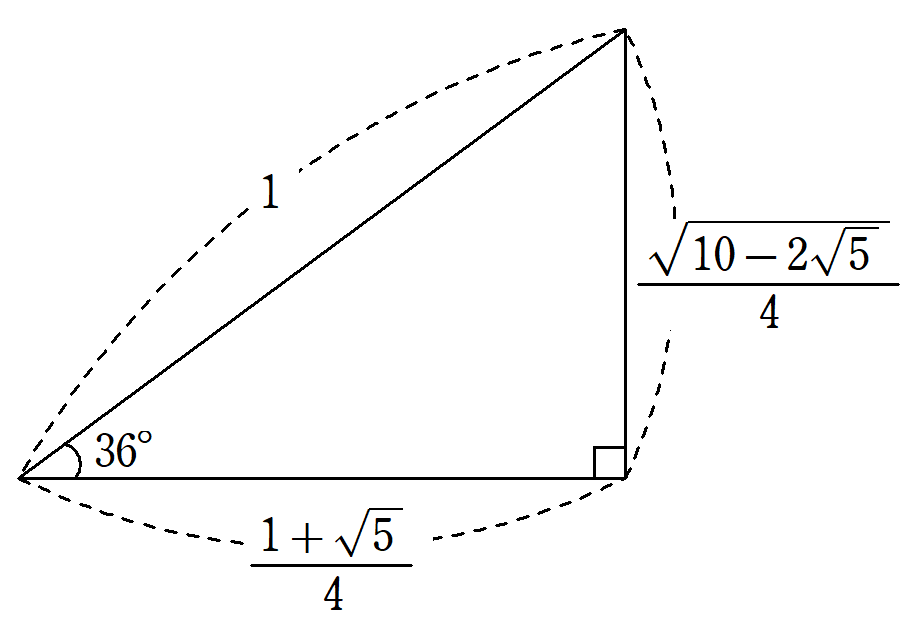数学ⅠA修了– tax –
-

無理数を発見したから殺された?ヒッパソスがピタゴラス学派に与えた影響を解説!【数学史6-8】
分数で表せない無理数。世の中の数はすべて有理数であることを主張していたピタゴラス教団において、同教徒であるヒッパソスが証明した無理数の存在は脅威となりました。この記事では、ヒッパソスがどのように証明を見つけ、その後どんな悲運な末路を送ったのかを解説します。 -

【証明あり】単位分数分解のやり方を解説!単位分数の和は無限通りに表せる!
分数を単位分数の和で表す「単位分数分解」。実は、単位分数分解は機械的かつ無限通りに行うことができます。この記事では、分解の方法を2種類解説するだけでなく、どんな分数でも無限通りに単位分数分解できる理由をしっかりと証明。例をたくさん使っているため、理解しやすい記事となっています。 -

【数学史3-7】ピタゴラスの定理はバビロニアが最初?粘土板の表に隠された秘密とは?
紀元前1800年頃のバビロニアでは、すでに三平方の定理が知られていました。ピタゴラスの誕生が紀元前6世紀なので、彼の1000年以上前に研究されていたことになります。その根拠となる粘土板や、そこに書かれていたピタゴラス数の求め方について、この記事では解説します。 -

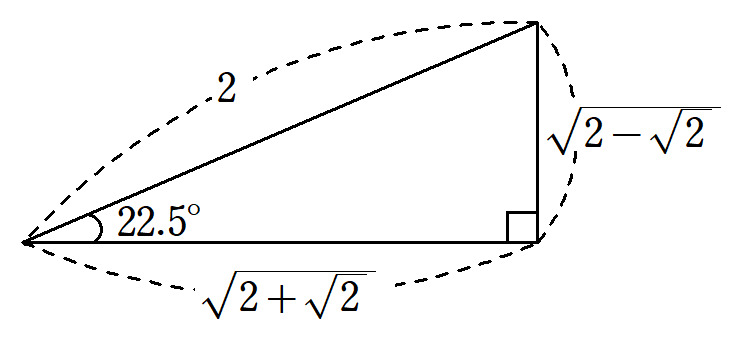
22.5°の三角比 ~半角の公式を使わずに、sin22.5°, cos22.5°, tan22.5°を求める方法を解説!~
22.5°の三角比は近似値を使わずに、値を表すことができます。これらの値がどのように求まるのかを、現役数学教員が2通りの方法で解説。この記事を読むことで、数学Ⅱの半角の公式を使わずに、数学Ⅰまでの知識で値を求める方法がわかります。 -

18°の三角比 ~黄金三角形からsin18°, cos18°, tan18°の値の求める方法を解説~
18°の三角比は近似値を使わずに、値を表すことができます。これらの値がどのように求まるのかを、現役数学教員が解説。この記事を読むことで、36°の三角比から半角の公式を用いる方法、黄金三角形から直接cos18°を求める方法の2種類について理解することができます。 -

15°の三角比~sin15°, cos15°, tan15°の値の求め方を3種類解説! 加法定理、半角の公式、直角三角形で導ける!~
15°の三角比は近似値を使わずに、値を表すことができます。これらの値がどのように求まるのかを、現役数学教員が解説。この記事を読むことで、三角関数の加法定理や半角の公式を使う方法だけでなく、幾何的に求める方法まで理解することができます。 -

36°の三角比 ~黄金比からsin36°, cos36°, tan36°の値を求める方法を解説!~
36°の三角比は近似値を使わずに、値を表すことができます。これらの値がどのように求まるのかを、現役数学教員が解説。値を求める鍵は、古来から人間を魅了してきた黄金比です。この記事を読むことで、黄金比の計算が36°の三角比にとう繋がっているかがわかります。 -

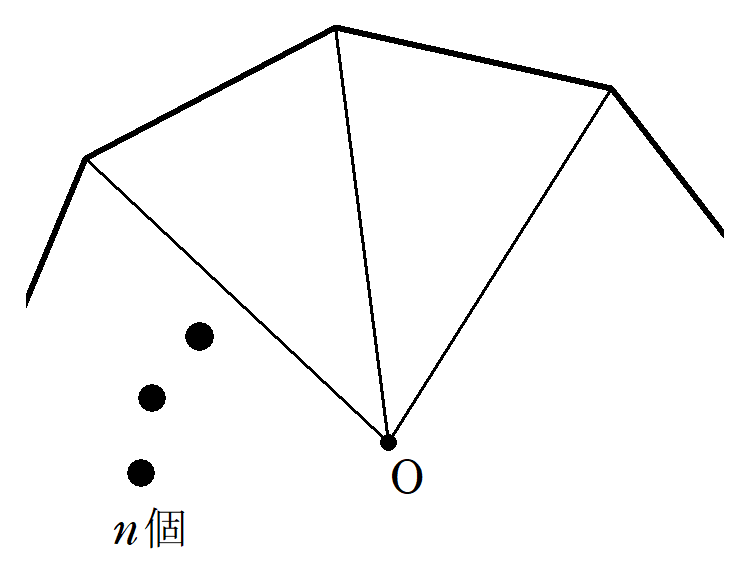
正多角形の面積の公式~一辺 a の正 n 角形の面積は1つの式で表せる!~
正四角形(正方形)の面積は簡単に求まりますが、正三角形や正五角形はどのように求められるでしょうか? 実は、どんな正多角形も1つの公式に代入することで求めることができます。この記事では、その公式の例や求め方について、現役数学教員が解説していきます。 -

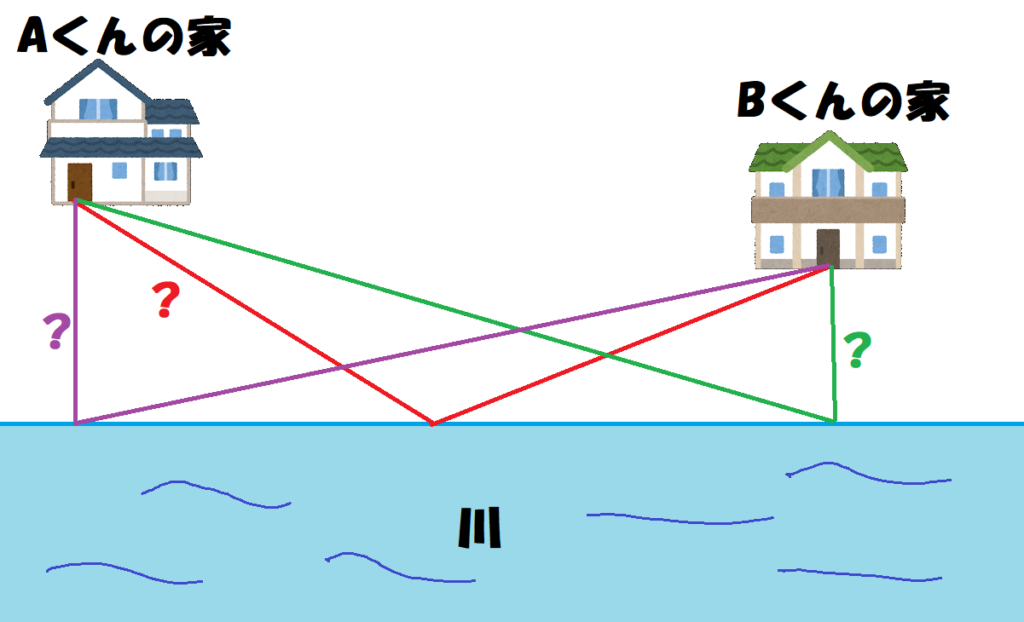
折れ線の最短距離
折れ線の最短距離は、線対称な位置に点をずらし、直線で結ぶことで求まります。 この記事では、なぜその作図方法が最短になるのかを証明します。 Ⅰ 最短距離の作図... -

1/81や1/9801の秘密
小数にすると、興味深い数列が並ぶ $~\displaystyle \frac{1}{81}~$ や $~\displaystyle \frac{1}{9801}~$ 。どのような数列となり、またなぜそのような数列が生まれ...
12