折れ線の最短距離は、線対称な位置に点をずらし、直線で結ぶことで求まります。
この記事では、なぜその作図方法が最短になるのかを証明します。
Ⅰ 最短距離の作図方法
Ⅱ 最短になる理由
Ⅰ 最短距離の作図方法
今回扱う問題は、次のような問題です。
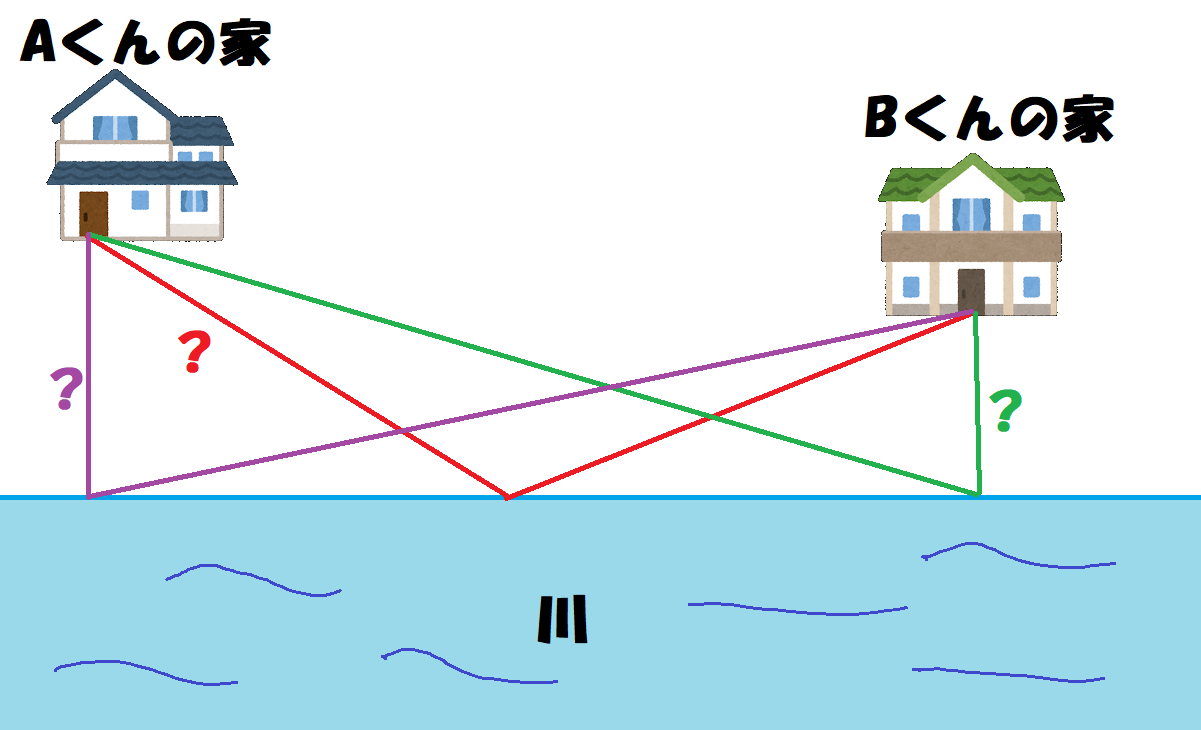
A君は家を出発して川で水を汲んでからB君の家に向かうことにした。川のどこで水を汲めば、道のりが最も短くなるでしょうか。
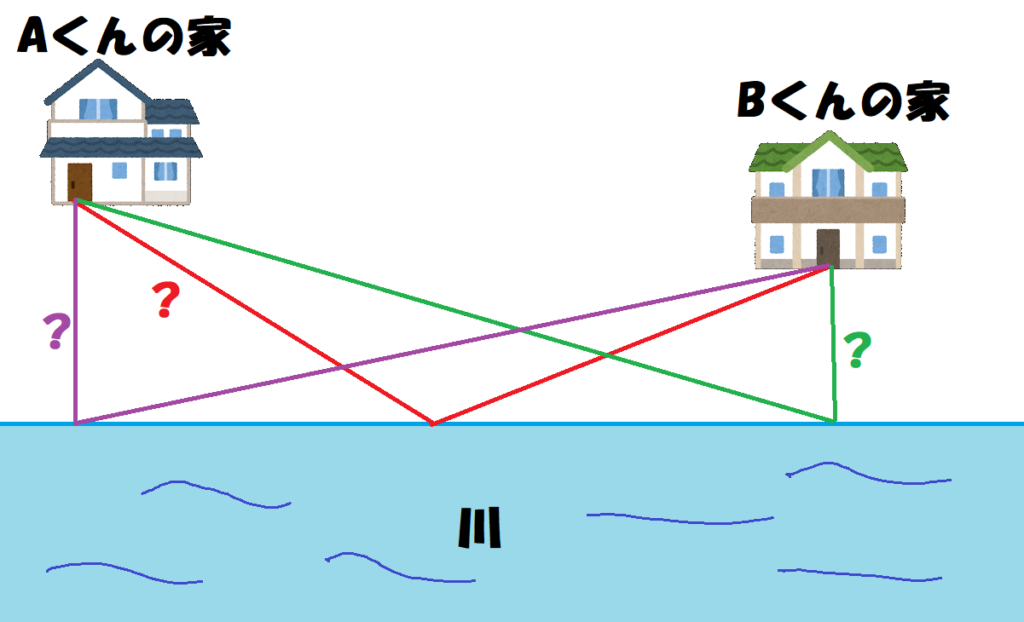
紫のルートだと、川までの距離は近いけど、その後の距離が長くなり、
緑のルートだと、水を汲んだ後は近いけど、川までの距離が長くなります。
川までの距離、水を汲んでからの距離が均等そうなのは、赤のルートですが、必ずしも他のルートより短いという保証はありません。
解き方を知らないと、なかなか難しい問題だと思います。
この問題を考えるにあたって、数学チックな問題の書き方にすると、次のような問題になります。
2点 $~A,B~$ が直線 $~XY~$ に関して同じ側にあるとき、 $~XY~$ 上の点 $~P~$ で、 $~AP+PB~$ が最も小さくなる点を求めなさい。
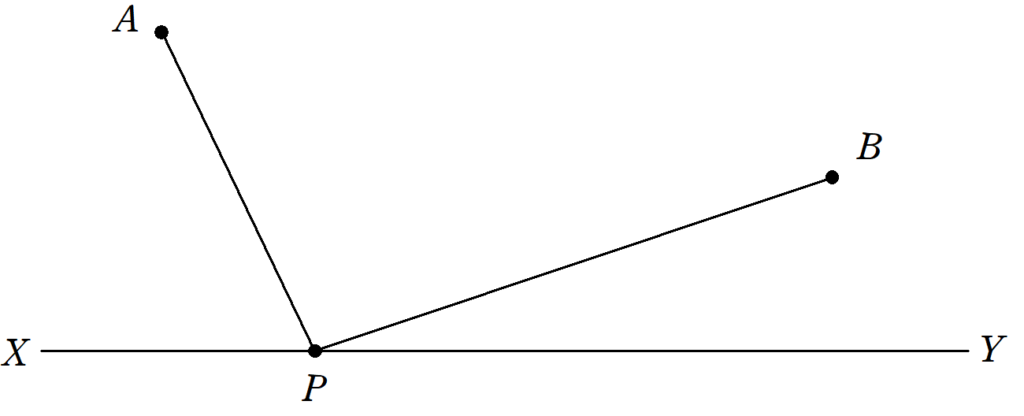
求め方に関しては中1の教科書にも載っているレベルですが、原理まできちんと考えると高1(数A)レベルの問題です。
この問題を見たことが無い、解き方を忘れた人は是非考えてみてください。
ということで、解答を示します。
・解答1
直線 $~XY~$ に関して、 $~A~$ と対称な点を $~A’~$ とし、線分 $~A’B~$ と $~XY~$ の交点を $~P~$ とすればよい。
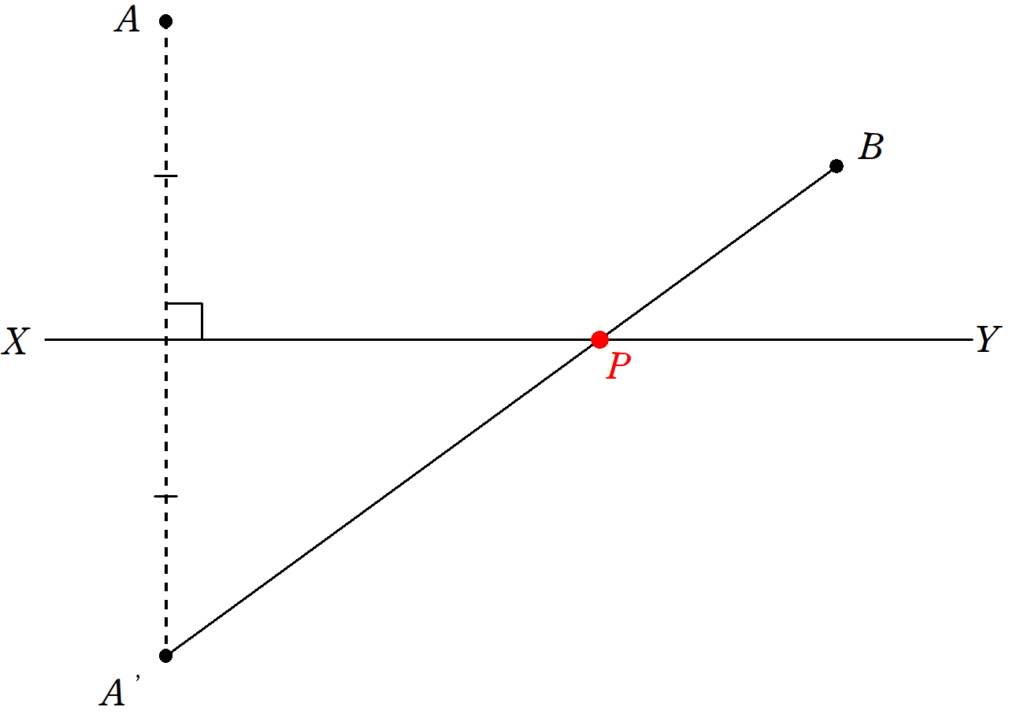
・解答2
直線 $~XY~$ に関して、 $~B~$ と対称な点を $~B’~$ とし、線分 $~AB’~$ と $~XY~$ の交点を $~P~$ とすればよい。
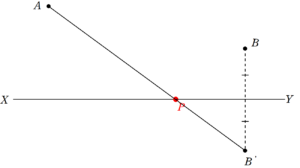
$~A~$ か $~B~$ を直線 $~XY~$ に関して対称移動させ、もう一方の点と結んであげれば $~P~$ の位置が決まるということですね。
では、なぜこのような作図で求まった $~P~$ のとき、 $~AP+PB~$ が最短になるのでしょうか?
この疑問をあの関係式を使って解決していきましょう。
Ⅱ 最短になる理由
証明で使う重要な関係式は、高1(数A)で登場する「三角不等式」です。
今回は先ほどの解答1のパターンについて証明します。(解答2のほうも同様に証明できます)
先ほどの図において、 $~AP~$ を結ぶ。
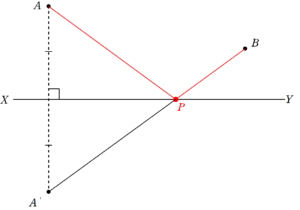
このとき、合同な三角形(2組の辺とその間の角がそれぞれ等しい)であることから、 $~AP=A’P~$ となる。・・・①
次に、直線 $~XY~$ 上に、 $~P~$ と異なる点 $~P’~$ を作る。
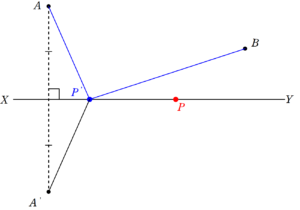
このとき、合同な三角形(2組の辺とその間の角がそれぞれ等しい)であることから、 $~AP’=A’P’~$ となる。・・・②
$~AP+PB~$ が最短となるためには、 $~AP+PB < AP'+P'B~$ を示せばよい。
①より、 $~AP+PB=A’P+PB=A’B~$ ・・・③。
②より、 $~AP’+P’B=A’P’+P’B~$ ・・・④。
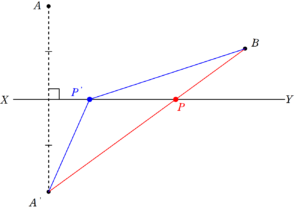
$~\triangle A’P’B~$ において三角不等式を使うと、
\begin{equation}
A’B < A'P'+P'B
\end{equation}
③、④より、
\begin{equation}
AP+PB < AP'+P'B
\end{equation}
が示された。 $~\blacksquare~$
$~P~$ 以外のどこに点 $~P’~$ を打っても、 $~P~$ を経由したほうが短いことが示せたので、 $~AP+PB~$ が最短ということになります。
三角不等式を使うことで、簡単に証明できました。
三角不等式、こういった場面でも役に立つんですね!!

◇参考文献等
・(2016)『新しい数学1』,p.149,東京書籍.
コメント