3×3の正方形に数を埋めて、全ての縦・横・斜めの和が等しくなるのが通常の魔方陣ですが、今回は縦・横・斜めの積が等しくなる「積の魔方陣」について考えます。
Ⅰ 積の魔方陣の定義
Ⅱ 指数法則を使った積の魔方陣
Ⅲ 最小の積の魔方陣
★魔方陣の関連記事はこちら↓★
・「3×3の魔方陣の作り方」
・「3×3魔方陣のもつ性質」
・「3×3魔方陣のすごい性質」
・「3×3×3の立方陣」(立体バージョンの魔方陣)
Ⅰ 積の魔方陣の定義
まず、数学における魔方陣について知らない方のために、元々の定義を載せておきます。
魔方陣は、 $~n \times n~$ 個の正方形の方陣に数字を配置し、縦・横・対角線のいずれの列についても、その列の数字の合計が同じになるもののことである。特に1から方陣のマスの総数 $~n^2~$ までの数字を1つずつ過不足なく使ったものを言う。(Wikipediaより)
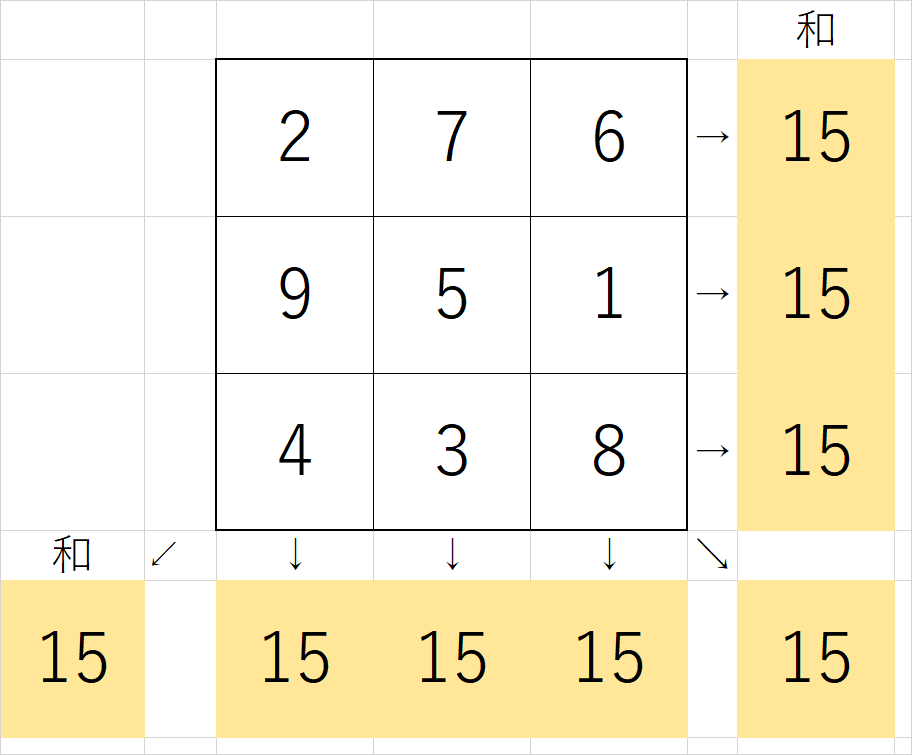
例えば、3×3で、1から9までの数字を使用して作った魔方陣は下のように作ることができます。
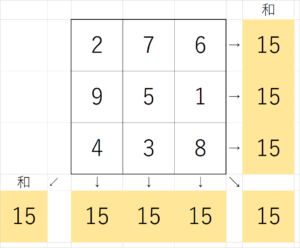
縦・横・斜めの和が全て15になっているのが確かめられます。
では、本題の積の魔方陣について考えてみましょう。まずは積の魔方陣の定義を次のようにしてみました。
積の魔方陣は、 $~n \times n~$ 個の正方形の方陣に数字を配置し、縦・横・対角線のいずれの列についても、その列の数字の積が同じになるもののことである。ただし、使う数は全て異なる自然数とする。
和のときと違って、連続した自然数では積の魔方陣を構成することはできません。使用する自然数をうまく選んであげることが重要になってきます。
Ⅱ 指数法則を使った積の魔方陣
実は、「積の魔方陣を1つ作りなさい」と言われれば、簡単に作ることができます。それがこちら。
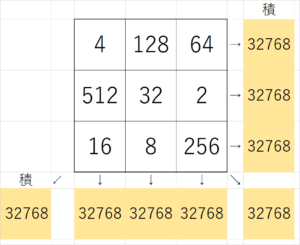
この魔方陣は指数法則 $~a^m \cdot a^n=a^{m+n}~$ を使って作られたものです。使われている数を $~2^n~$ の形で表してみると、
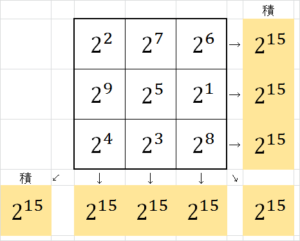
となり、指数の部分が先ほどの和の魔方陣の例と一致していることが確かめられます。
この考え方を使えば、いくらでも積の魔方陣を作ることができるでしょう。
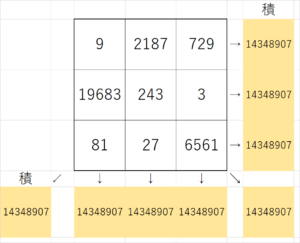
ということで、3のべき乗バージョンも作ってみました。ただ、合計の数がとんでもなく大きな数 $~(3^{15})~$ になってしまいました。
Ⅲ 最小の積の魔方陣
確かに指数法則を使えば、簡単に積の魔方陣が作れるとわかりましたが、数が膨大であまり美しくないですね。そこで、縦・横・斜めの積が最小となるような魔方陣について考えてみました。
縦・横・斜めの積が最小となる積の魔方陣は、次のように与えられる。
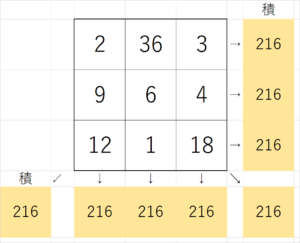
確かに、先ほどの2のべき乗の魔方陣よりも圧倒的に小さくなりました。積の魔方陣のルールも満たしています。しかし、これが本当に最小なのでしょうか。この魔方陣が最小と言える理由を証明してみましょう。
魔方陣の中身を次のように9つの文字で置く( $~a~i~$ は互いに異なる自然数)。また、縦・横・斜めの積をそれぞれ $~P~$ とする。
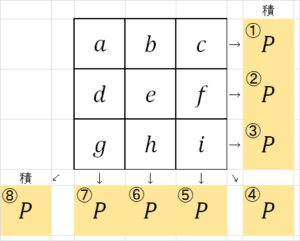
この魔方陣において、次の8つの等式が成り立つ。
\begin{align}
abc&=P・・・① \\
def&=P・・・② \\
ghi&=P・・・③ \\
aei&=P・・・④ \\
cfi&=P・・・⑤ \\
beh&=P・・・⑥ \\
adg&=P・・・⑦ \\
ceg&=P・・・⑧ \\
\end{align}
②、④、⑥、⑧の両辺をすべて掛け合わせると、
\begin{align}
(def)(aei)(beh)(ceg)&=P^4 \\
abcde^4fghi&=P^4 \\
abcdefghi\cdot e^3 &=P^4 \\
(abc)(def)(ghi)\cdot e^3&=P^4 \\
\end{align}
ここで、①、②、③を代入すると、
\begin{align}
P \cdot P \cdot P \cdot e^3&=P^4 \\
e^3&=P \\
\end{align}
が求まる。この式より、縦・横・斜めの積 $~P~$ は立方数であることがわかった。
ここで、 $~P~$ について考える。
$~P~$ は①~⑧の式で作られるため、 $~a~f~$ は $~P~$ の約数であることがわかる。また、 $~a~f~$ は異なる自然数であるため、 $~P~$ は9つ以上の約数を持つ立方数であることが言える。この条件を満たす最小の自然数 $~P~$ を探す。
(1) $~e=1~$ のとき、
$~P=e^3=1~$ であり、1の約数は1個のため、不適。
(2) $~e=2~$ のとき、
$~P=e^3=2^3~$ であり、 $~2^3~$ の約数は4個のため、不適。
(3) $~e=3~$ のとき、
$~P=e^3=3^3~$ であり、 $~3^3~$ の約数は4個のため、不適。
(4) $~e=4~$ のとき、
$~P=e^3=4^3=2^6~$ であり、 $~2^6~$ の約数は7個のため、不適。
(5) $~e=5~$ のとき、
$~P=e^3=5^3~$ であり、 $~5^3~$ の約数は4個のため、不適。
(6) $~e=6~$ のとき、
$~P=e^3=6^3=(2 \cdot 3)^3=2^3 \cdot 3^3 ~$ であり、 $~2^3 \cdot 3^3~$ の約数は16個のため、魔方陣ができる可能性がある。
$~e=6,P=6^3=216~$ を使って、残りのマスを埋めてみる。

これは魔方陣の条件を満たすため、最小の積の魔方陣が求まった。 $~\blacksquare~$
マスに入る数は異なる自然数であることと、等式の性質を隈なく使ってあげることで、一見難しそうな最小であることの証明もできました。
前々から普通の魔方陣はよく知っていましたが、『笑う数学』にこの積の魔方陣が載っていてびっくり!ここに載っていた最小の積の魔方陣に証明を与えられたので満足です(^^)

◇参考文献等
・日本お笑い数学協会(2018)『笑う数学』,pp.28-30,KADOKAWA.
・「Wikipedia」,<https://ja.wikipedia.org/wiki/%E9%AD%94%E6%96%B9%E9%99%A3 > 2018年3月12日アクセス
コメント