-

【数学史まとめ5】古代中国の数学
四大文明の一つで長い歴史を持つ中国。 しかし、紀元前213年の焚書政策により、紀元前の数学関係の資料はほとんど失われてしまいました。 そのため、古代中国の数... -

【数学史まとめ4】古代インドの数学
四大文明の1つとして有名なインダス文明を起源とする古代インド。インダス文字の解読が進んでいないため、現在わかっている最古のインド数学は、紀元前1000年頃の儀式書『シュルバスートラ』を読み解いたものとなっています。この記事では、古代インド数学の発展に関する出来事を年表形式でまとめるとともに、その内容をざっくり解説します。 -

三平方の定理の証明⑯~2023年最新!三角比を用いた証明をわかりやすく解説! 発見者は10代の少女?~
この記事では、数ある三平方の定理の証明の中でも、2023年最新の証明方法を紹介します。循環論法になりやすい三角比を使った珍しい証明方法です。話題になっている方法をどこよりもていねいに解説しています。 -

【証明あり】単位分数分解のやり方を解説!単位分数の和は無限通りに表せる!
分数を単位分数の和で表す「単位分数分解」。実は、単位分数分解は機械的かつ無限通りに行うことができます。この記事では、分解の方法を2種類解説するだけでなく、どんな分数でも無限通りに単位分数分解できる理由をしっかりと証明。例をたくさん使っているため、理解しやすい記事となっています。 -

【教員向け】数学の授業で使える小ネタ集2(中1「文字と式」)
数学の授業に悩んでいる教員必見!授業準備に十分な時間がとれなくても、数学の小ネタを授業の中で入れることで、生徒が面白いと思える授業にしていくことができます。この記事では、中学数学の2つめの単元である「文字と式」に絡めた数学小ネタを紹介!生徒の笑いや「へぇ」を導き出す小ネタを仕入れて授業に臨みましょう! -

【教員向け】数学の授業で使える小ネタ集1(中1「正負の数」)
数学の授業に悩んでいる教員必見!授業準備に十分な時間がとれなくても、数学の小ネタを授業の中で入れることで、生徒が面白いと思える授業にしていくことができます。この記事では、中学数学の最初の単元である「正負の数」に絡めた数学小ネタを紹介!生徒の笑いや「へぇ」を導き出す小ネタを仕入れて授業に臨みましょう! -

2023はどんな数?素因数分解や約数、2023を含む数列を解説!
2023ってどんな数?2023は素数なの?という疑問に答えます!実は、2023は7や17で割りきれるため、素数ではありません。しかし、幸運数やハーシャッド数、ピタゴラス数にはあてはまっています。2023年の始まりにふさわしい、縁起の良さそうな式も紹介しているため、この記事を読むことで2023に親しみを持つことができます。 -

ヒポクラテスの三日月~定理の内容や証明をわかりやすく解説!応用例も紹介!~
中学受験で登場する「ヒポクラテスの定理」。この定理は今から約2500年前に生まれ、曲線図形の面積が直線図形の面積と等しくなるという観点から、当時のギリシャに大きな衝撃を与えました。この記事では、その歴史について触れながらも定理の内容やその証明、応用例について解説します。 -

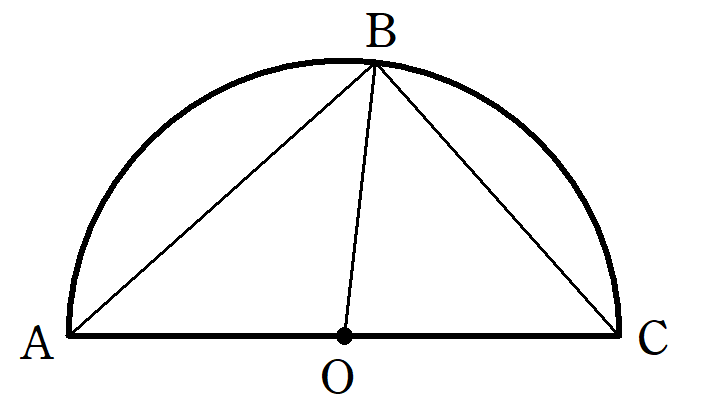
タレスの定理~中学3年生で習う円の定理を解説!証明は超簡単!~
世界で最初に証明された定理は「タレスの定理」であり、「半円に内接する三角形は直角三角形である」という内容です。実は、タレスの定理と呼ばれる定理は他にもあり、すべて現在の中学レベルの内容でした。それらの紹介と共に、タレスの定理が後世の数学にどのような影響を与えたのかを解説します。 -

【数学史まとめ3】バビロニアの数学
メソポタミアの数学のことを、数学史上では「バビロニアの数学」と言い表します。紀元前1750年頃に数体系が確立していたバビロニア。実生活で使う範囲を超えた数学の記録が粘土板に今も残っています。この記事では、バビロニアの数学に関する事柄を年表形式でまとめると共に、バビロニアが紀元前に誇った高度な数学を大まかに解説します。