三平方の定理の証明は、紀元前からあらゆる人があらゆる方法で考え出してきました。
この記事では、その中でも相似を利用した簡単な証明方法について、現役数学教員がわかりやすく解説します。
実は、たった1本の補助線だけで三平方の定理は証明ができるんです!
しかも、紹介する2つの証明方法のうち、1つは物理学者アインシュタインが少年時代に考案したもの。
また、中3では相似分野の直後に三平方の定理へと入るので、単元の導入としても扱いやすい証明方法です。
この記事を読んで、相似と三平方の定理を繋げてしまいましょう。
- 物理学者アインシュタインについて
- アインシュタインが考案した面積比を用いた証明方法
- 相似を利用した最も簡単な証明方法
三平方の定理の内容や、三平方の定理の別証についてはこちらから↓↓

アインシュタインについて
アルベルト・アインシュタイン(Albert Einstein , 1879-1955)は、ドイツ生まれの物理学者です。

(出典:Ferdinand Schmutzer, Public domain, via Wikimedia Commons)
アインシュタインは1891年12歳のとき、幾何の本を貰い、非常に喜びながら読みふけりました。
彼はその本を「幾何の小聖書」と呼ぶほど愛着を持っていて、その後三平方の定理についての勉強を必死にしました。
その大変な努力の後、1895年にアインシュタインは面積比に基づく証明方法を考案しました。

ちなみに、1905年に発表した特殊相対性理論や、1916年に発表した一般相対性理論といった、彼の代表的な理論の中でも三平方の定理は使われています。
相似を利用した簡単な証明1(アインシュタインの証明)
必要な補助線は1本だけ!
非常にシンプルな証明方法です。
直角三角形$~ABC~$で、直角をもつ頂点$~C~$から斜辺$~BA~$に向け垂線$~CH~$を引く。
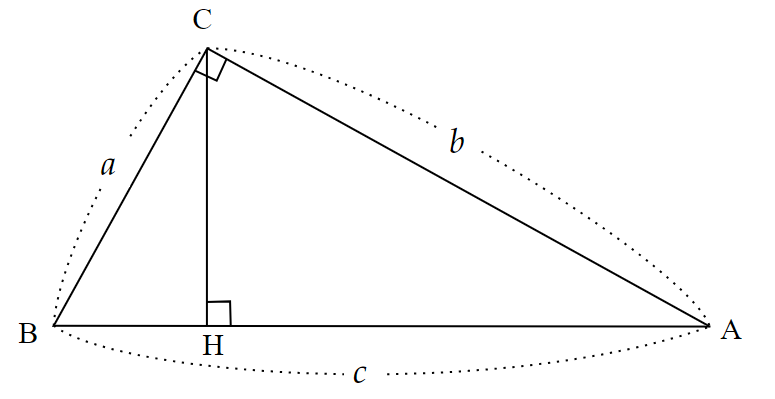
このとき、直角と共通な角より、2組の角がそれぞれ等しいので、
$\triangle ABC~$∽$~\triangle CBH ~~~~\cdots ~①$
$\triangle ABC~$∽$~\triangle ACH ~~~~\cdots ~②$
であり、$①$と$②$をまとめると、
$\triangle ABC~$∽$~\triangle CBH~$∽$~\triangle ACH ~~~~\cdots ~③$
となる。
これらの直角三角形のそれぞれの斜辺から、相似比は$~c~:~a~:~b~$。
そのため、面積比は $~c^2~:~a^2~:~b^2~$となる。
したがって、3つの直角三角形の面積は、正の数$~k~$を用いて、
\triangle ABC=c^2k \\ \triangle CBH=a^2k \\ \triangle ACH =b^2k
と表せる。
図3から、 $\triangle ABC=\triangle CBH=\triangle ACH~$であるため、
\begin{align*}
c^2k=a^2k+b^2k \\
c^2=a^2+b^2
\end{align*}と三平方の定理が求まった。■
相似な図形の面積比や体積比が、相似比の2乗、3乗であることは、中3相似分野の最後のほうで習うので、三平方の定理の接続としても扱いやすいです。
アインシュタインの証明という点も、生徒の興味を惹きやすいですね。
相似を利用した簡単な証明2
アインシュタインと同じ補助線で、面積比ではなく線分比から証明する方法です。
直角三角形$~ABC~$で、直角をもつ頂点$~C~$から斜辺$~BA~$に向け垂線$~CH~$を引く。
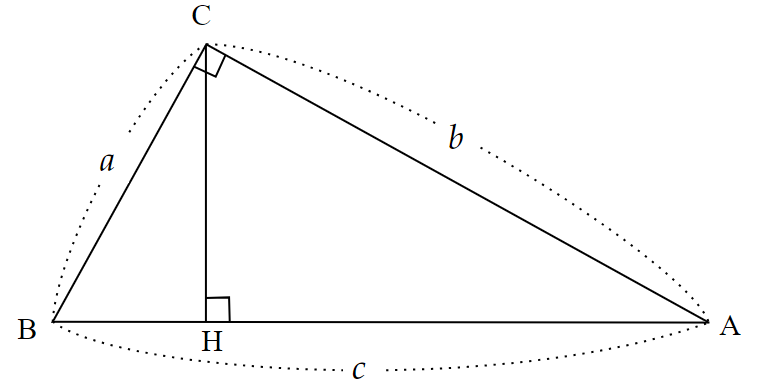
このとき、直角と共通な角より、2組の角がそれぞれ等しいので、
$\triangle ABC~$∽$~\triangle CBH ~~~~\cdots ~①$
$\triangle ABC~$∽$~\triangle ACH ~~~~\cdots ~②$
である。
$①$より、
\begin{align*}
AB : CB &= BC : BH \\
BC^2 &= AB \cdot BH \\
a^2 &= c \cdot BH ~~~\cdots ③
\end{align*}であり、同様に$~②~$より、
\begin{align*}
AB : AC &= AC : AH \\
AC^2 &= AB \cdot AH \\
b^2 &= c \cdot AH ~~~\cdots ④
\end{align*}が求まる。
$③~,~④$より、
\begin{align*}
a^2+b^2&=c \cdot BH +c \cdot AH \\
&=c(BH+AH) \\
&=c \cdot AB \\
&=c^2
\end{align*}と三平方の定理が求まった。■
この証明方法は多くの書物に掲載されている、三平方の定理の代表的な証明方法です。
インドのバスカラ(Bhaskara , 1114~1185頃)やイギリスのジョン・ウォリス(John Wallis , 1616~1703)の証明とも言われています。

(出典:After Godfrey Kneller, Public domain, via Wikimedia Commons)
しかし、古くから存在していたことから、ピタゴラス(Pythagoras , B.C.569頃~B.C.500頃)もこの方法を知っていたのではないかという考え方もあります。


アインシュタインの証明、これだけ単純だと、もっと前に発見されているようにも思えるけど……。



実際、似たような証明はユークリッドの『原論』6巻の命題31にあったよ。
三平方の定理の内容や、三平方の定理の別証についてはこちらから↓↓



コメント
コメント一覧 (4件)
ご返信ありがとうございます。
数学は答え(結果)だけでなく、いろいろな途中経過を考えることも大切で楽しいことを子供たちに知ってほしいと思います。
今後もよろしくお願いいたします。
先ほどコメントした奥平ですが、一部文章にあやまりがありました。
先頭の部分は、“線分ACと点Bからの垂線の交点をDとし・・・”の誤りです。
お詫びして訂正いたします。
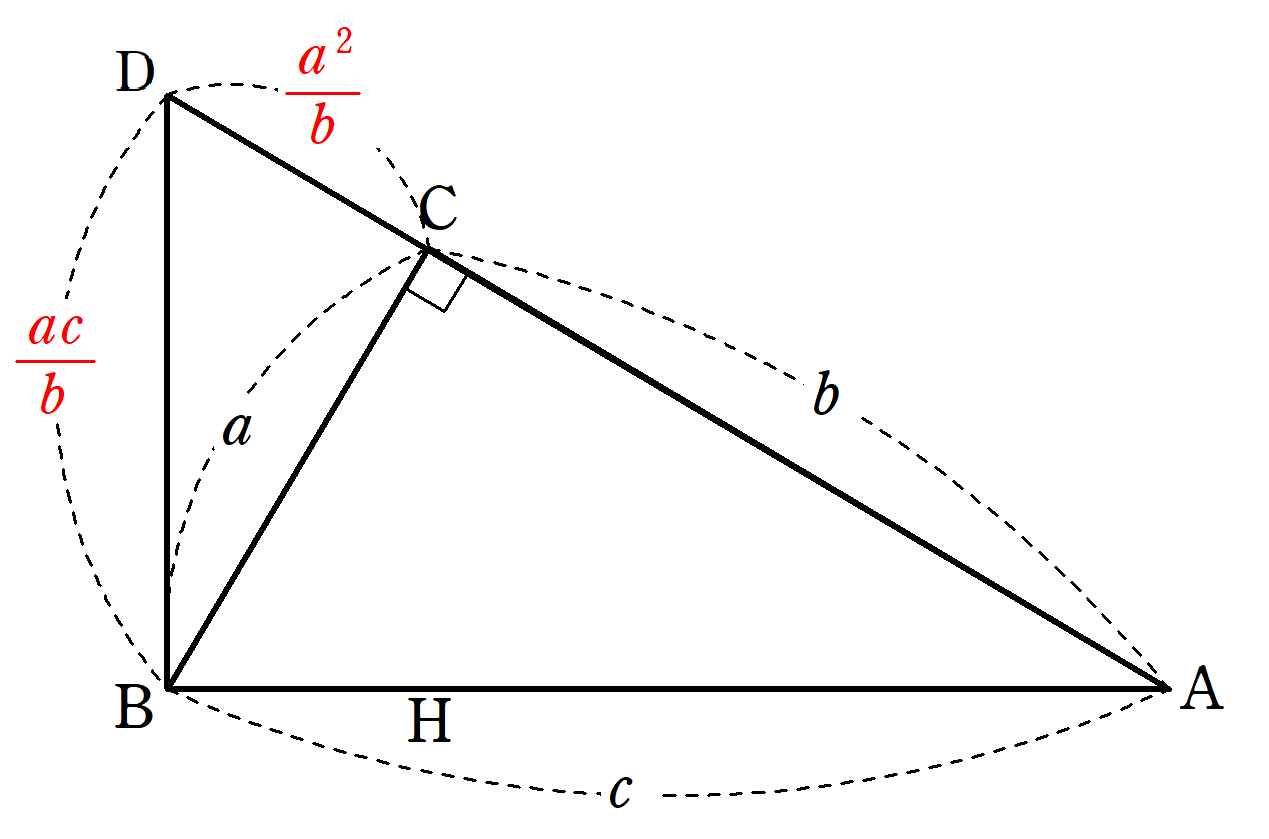
似たような方法ですが、以下ご参考まで。
図4の直角三角形ABCにおいて、線分ACと線分BDの延長線の交点をDとすると
△ABC∽△BDC となるので、BD=ac/b、DC=a^2/b
△ABC+△BDC=△ADB だから、ab/2 + (a^2/b)*a/2=(ac/b)*c/2
よって、
b^2 + a^2=c^2
奥平様
コメントありがとうございます。
延長して相似な三角形を作り、面積に着目する方法面白かったです!
今後ともよろしくお願いします。