三平方の定理の証明は、紀元前からあらゆる人があらゆる方法で考え出してきました。
この記事では、その中でも数学Aで登場する方べきの定理を利用する証明方法について、現役数学教員がわかりやすく解説します。
方べきの定理は３種類ありますが、そのうちの２種類を三平方の定理の証明に利用することができます。
特定の図で、方べきの定理を適用するだけの方法なので、図の作り方をこの記事で覚えましょう。
- 方べきの定理の概要とその歴史
- 方べきの定理を利用した三平方の定理の証明方法２種
三平方の定理の内容や、三平方の定理の別証についてはこちらから↓↓
方べきの定理とその歴史
方べきの定理３パターン
方べきの定理は、円と２本の直線に関する定理で、３パターン存在します。
まずは、その３パターンの内容について、復習しておきましょう。
円の内部の点$~P~$を通る2本の弦$~AB~$と弦$~CD~$に関して、次の等式が成り立つ。
PA \cdot PB= PC \cdot PD
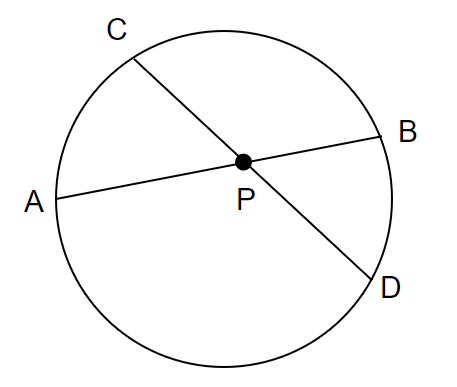
１パターン目は、２直線が円の内部で交わるタイプ。
証明は、円周角の定理から導かれる$~\triangle PAC$∽$\triangle PDB~$を使います。
円の内部の点$~P~$を通る2本の弦$~AB~$と弦$~CD~$に関して、次の等式が成り立つ。
PA \cdot PB= PC \cdot PD
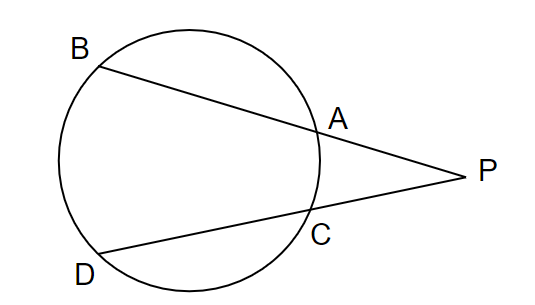
２パターン目は、２直線が円の外部で交わるタイプ。
証明は、内接四角形の性質から導かれる$~\triangle PAC$∽$\triangle PDB~$を使います。
円の外部の点$~P~$から円に引いた接線の交点を$~T~$とする。
$~P~$を通り、この円と２点$~A~,~B~$で交わる直線を引くと、次の等式が成り立つ。
PT^2= PA \cdot PB
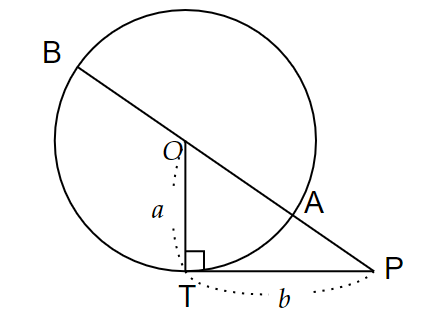
３パターン目は、２直線が円の外部で交わり、そのうちの１直線が接線のタイプ。
証明は、接弦定理から導かれる$~\triangle PAT$∽$\triangle PTB~$を使います。
以上の３パターンのうち、三平方の定理の証明に使えるのは方べきの定理１と方べきの定理３の２パターン。
証明に入る前に、方べきの定理がいつから存在していたのかを見てみましょう。
方べきの定理の歴史
方べきの定理は紀元前から存在していました。
その理由は、ユークリッドの『原論』の第３巻の命題35、36に方べきの定理の主張があるからです。
円の内部の点$~P~$を通る弦がその円と交わる点を$~A~$と$~B~$とするとき、積$~PA\times PB~$は一定である——$~P~$を通るあらゆる弦に対して同じ値をとる。
円の外部の点$~P~$を通る弦がその円と交わる点を$~A~$と$~B~$とするとき、積$~PA\times PB~$は$~PT^2~$に等しい。ここで$~PT~$は$~P~$から円への接線の長さである。
多少表現は違いますが、命題３５が方べきの定理１、命題３６が方べきの定理２の内容となっています。
『原論』は、 当時の初等数学全体を体系的に網羅していて、その後の時代にも大きな影響を与えた名著です。
ユークリッド（Euclid , B.C.330頃-B.C.275頃） が紀元前300年頃に書いたものになります。
（出典：Photograph taken by Mark A. Wilson (Wilson44691, Department of Geology, The College of Wooster).[1], Public domain, via Wikimedia Commons）
![Photograph taken by Mark A. Wilson (Wilson44691, Department of Geology, The College of Wooster).[1]](https://commons.wikimedia.org/wiki/File:EuclidStatueOxford.jpg){kind=link}
これから解説する三平方の定理の証明方法は、誰がいつ発見したかは定かではありません。
しかし、特定の図を作って方べきの定理を適用してあげるだけなので、早ければ『原論』が出版された紀元前300年頃から存在していたものかもしれません。
方べきの定理を利用した証明１
では、本題である三平方の定理の証明に入りましょう。
半径$~c~$の円$~O~$で、直径を$~AB~$とする。
$~AB~$上で中心から$~a~$離れている点を$~P~$とし、$~P~$を通り$~AB~$と垂直な弦$~CD~$を作り、$~CP~$の長さを$~c~$とする。
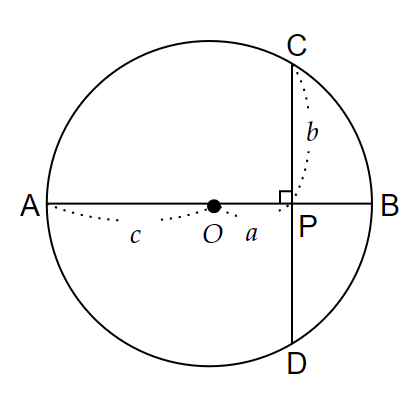
$~PC=PD~$より、$~PD=b~$。
$~OB~$は半径なので、$~PB=c-a~$とわかる。
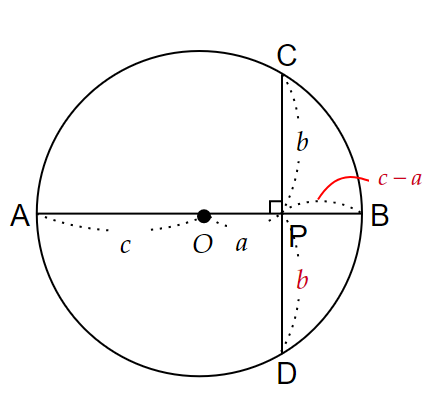
ここで、「方べきの定理１」を使うと、
\begin{align*}
PA \cdot PB&= PC \cdot PD \\
(c+a)\cdot (c-a)&=b \cdot b \\
c^2-a^2&=b^2 \\
c^2&=a^2+b^2 ~~~~\cdots ①
\end{align*}が求まる。
$~c~$は半径だったので、$~OC=c~$。
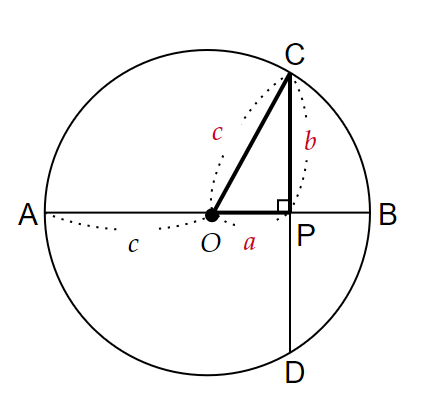
直角三角形$~OPC~$に注目すれば、$①$より三平方の定理が証明されたことが言える。■
円の中の等しい辺の長さをうまく利用しながら、方べきの定理１を用いた証明でした。
図５を覚えておくことで、自力でもこの証明方法を再現できるでしょう。
方べきの定理を利用した証明２
今度は接線型の方べきの定理３を利用した証明方法です。
半径$~a~$の円$~O~$で、円周上の点$~T~$における長さ$~b~$の接線$~AT~$を引く。
直線$~PO~$と円$~O~$の２つの交点をそれぞれ$~A~$と$~B~$とする。
$~PO=c~$とすると、各辺の長さは図３のようになる。
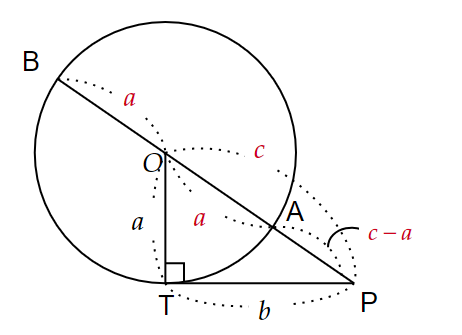
ここで、「方べきの定理３」を使うと、
\begin{align*}
PA^2 &= PB \cdot PC \\
b^2&=(c-a) \cdot (c+a) \\
b^2&=c^2-a^2 \\
a^2+b^2&=c^2 ~~~~\cdots ②
\end{align*}が求まる。
したがって、直角三角形$~PTO~$に注目すれば、$②$より三平方の定理が証明されたことが言える。■
こちらも図９を覚えておくことで、この証明を再現できます。
方べきの定理自体の証明方法の理解も忘れずに。
もしかしたらユークリッドが思いついた証明方法だったかもしれないね。
確かに。
ユークリッドは「花嫁の椅子」を使って、三平方の定理を証明しているから、思いついていたとしてもわざわざ載せたりしなさそう・・・。
三平方の定理の内容や、三平方の定理の別証についてはこちらから↓↓
コメント