三平方の定理の証明は、紀元前からあらゆる人があらゆる方法で考え出してきました。
この記事では、数学Ⅰの発展内容として扱われるトレミーの定理を用いた証明方法を、現役数学教員がわかりやすく解説します。
円に内接する長方形にトレミーの定理を適用するだけの簡単な証明方法なので、この記事を読んで三平方の定理の証明のバリュエーションを増やしましょう。
- トレミーの定理の概要とその歴史
- トレミーの定理を利用した三平方の定理の証明方法
三平方の定理の内容や、三平方の定理の別証についてはこちらから↓↓

トレミーの定理とは?
トレミーは誰のこと?
ローマ時代の数学者クラウディオス・プトレマイオス(Claudius Ptolemaeus , 85頃-165頃)は、トレミー(Ptolemy)とも呼ばれ、アレクサンドリアの地で科学の研究をしていました。

(出典:Unknown authorUnknown author, Public domain, via Wikimedia Commons)
天文学を科学的に考察するなかで、三角関数を研究するようになりました。
現在の教科書の巻末についている三角関数の表の元となる、正弦の表を作成しています。
その作成の際に多用したのが、彼の著書『アルマゲスト』に載っていたトレミーの定理です。
トレミーの定理の内容
プトレマイオス(トレミー)が三角比を考える際に利用したトレミーの定理。
円に内接する四角形の性質となっています。
円に内接する任意の四角形ABCDについて、次の等式が成り立つ。
AC \times BD=AB \times CD + BC \times DA
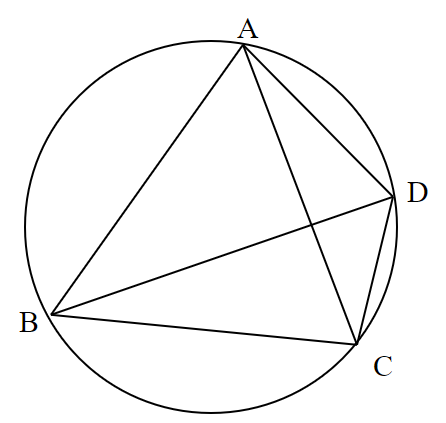
この定理は、2本の対角線の積は、2組の対辺の積の和に等しいということを表しています。
色分けして見やすくすると、次の図3のようになります。
$AC \times BD$$~=~$$AB \times CD$$~+~$$BC \times DA$
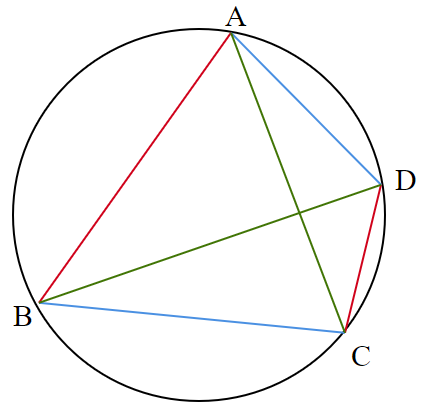
証明については、相似や余弦定理を使うことで可能です。
トレミーの定理による証明
トレミーの定理の証明さえできれば、これを利用した三平方の定理の証明自体は簡単にできます。
最初の図を覚えることで、いつでも導けるようになるでしょう。
図4のような、円に内接する長方形ABCDを考える。
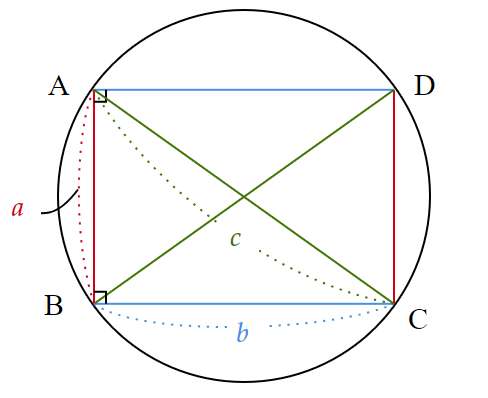
$~AB=a~$、$~BC=b~$、$~AC=c~$としたとき、トレミーの定理より、
$AC \times BD$$~=~$$AB \times CD$$~+~$$BC \times DA$
が成り立つ。
よって、$~BD=AC=c~$、$~CD=AB=a~$、$~DA=BC=b~$より、
\begin{align*}
c \times c &=a\times a+b \times b \\
c^2&=a^2+b^2
\end{align*}であることが示された。■
任意の内接四角形でトレミーの定理が成り立つため、長方形でトレミーの定理を適用するだけの証明でした。

なんで「プトレマイオス」が「トレミー」なの?



英語圏だと「マイケル」を「マイク」って呼ぶことあるよね?
それと同じ理由だよ。
三平方の定理の内容や、三平方の定理の別証についてはこちらから↓↓



コメント