平均値の定理を証明する上で必要なロルの定理。
数学の定理ではよくあることですが、書いてあることは当たり前のことでも、数式にするとわかりづらい内容となっています。
この記事では、ロルの定理の意味を例示で説明するとともに、ロルの定理の証明を解説!
ロルの定理が使えないパターンも示してあるため、定理の中身をしっかりと理解できます。
ロルの定理とは?
まずは、数学書にも載っているロルの定理の内容を知っておきましょう。
フランスの数学者が公表した定理
ロルの定理は、フランスの数学者ミッシェル・ロル(Michel Rolle , 1652-1719)が1690年に公表した、導関数に関する定理です。

(出典:See page for author, Public domain, via Wikimedia Commons)
ロルの定理を発見しただけでなく、$~x~$の$~n~$乗根を表す記号である$~\sqrt[n]{x}~$を発明したことでも有名な数学者です。
数学Ⅲの教科書には、ロルの定理が平均値の定理の特別な形として紹介されているものの、歴史的には以下のような順番で発見されています。
- ロルの定理(1690年)
- 平均値の定理(1797年)
- コーシーの平均値の定理(1823年)
そのため、ロルの定理を理解してから平均値の定理へと進んでいくことが自然な流れとなるでしょう。
ちなみに、コーシーの平均値の定理は数学Ⅲでは学ばないものの、平均値の定理をさらに一般化した定理となっています。
連続関数の微分に関する定理
数学書では、以下のようにロルの定理が説明されています。
閉区間 $~[a,b]~$ で連続、開区間 $~(a,b)~$ で微分可能な関数 $~f~$ に関して、 $~f(a)=f(b)~$ ならば $~f'(c)=0~$ を満たす $~c \in (a,b)~$ が存在する。
簡単に定理の内容を表現すると、以下のようになります。
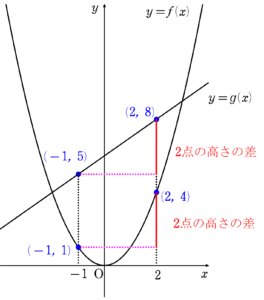
高さ $~y~$ が同じ点を2つ見つけると、その間には必ず微分係数が0になる点が存在する。
折り返し地点では必ず接線が$~x~$軸と平行という当たり前のことを表しているのがロルの定理です。
ロルの定理の例と誤用例
ロルの定理をビジュアル化した例を3つと、連続や微分可能性を無視してはいけない理由がわかる例2つを紹介します。
3つの関数にロルの定理を適用してみた
関数$~f(x)~~( a < x < b )~$を設定したうえで、$~f(c)=0~~( a < c < b )~$となる$~c~$がどんな値になるかを3つほど試してみました。
$~f(x)=x^2~~(a=-2,b=2)~$の場合
閉区間 $~[-2,2]~$ で連続、開区間 $~(-2,2)~$ で微分可能、 $~f(-2)=f(2)=4~$ である。
ロルの定理より、 $~-2~$ から $~2~$ の中で、微分係数が $~0~$ (すなわち、 $~x~$ 軸と平行)になるような点$~c~が存在する。
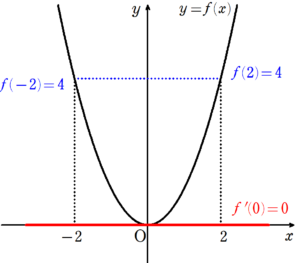
図2より、$~c=0~$のときに$~f'(c)=0~$ となっている。
例1からわかる通り、折り返し地点で微分係数が$~0~$になっています。
$~f(x)=\sin{x}(a=0,b=2 \pi )~$の場合
閉区間 $~[0,2 \pi]~$ で連続、開区間 $~(0,2 \pi)~$ で微分可能、 $~f(0)=f(2 \pi)=0~$ である。
ロルの定理より、 $~0~$ から $~2 \pi~$ の中で、微分係数が $~0~$ (すなわち、 $~x~$ 軸と平行)になるような点$~c~$が存在する。
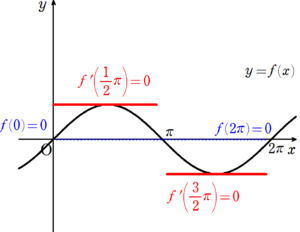
図3より、$~c=\displaystyle \frac{1}{2}\pi~,~\displaystyle \frac{3}{2}\pi~$のときに$~f'(c)=0~$ となっている。
例2のように、微分係数が $~0~$ になる点が複数になることもあります。
$~f(x)=x^3-6x^2+9(f(a)=f(b)=2)~$の場合
閉区間 $~[a,b]~$ で連続、開区間 $~(a,b)~$ で微分可能、 $~f(a)=f(b)=2~$ である。
ロルの定理より、 $~a~$ から $~b~$ の中で、微分係数が $~0~$ (すなわち、 $~x~$ 軸と平行)になるような点$~c~$が存在する。
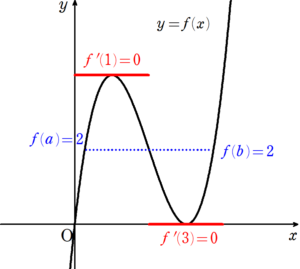
図4より、$~c=1,3~$のときに$~f'(c)=0~$となっている。
スタートとゴールの高さが同じなら、単調増加や単調減少にはならないため、折り返し地点(接線が$~x~$軸と平行な点)が必ず存在することがわかるでしょう。
連続性や微分可能性を無視した例
しかし、スタートとゴールが同じ高さだとしても、不連続や微分不可能な関数ではロルの定理は成り立ちません。
$~f(x)=\tan{x}(a=0,b=\pi)~$ の場合
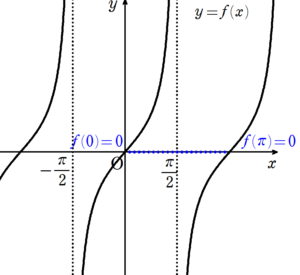
図5からわかる通り、$~f'(c)=0~$ となるような $~c \in (0,\pi)~$ は存在しない。
適用範囲に不連続な点 $~\displaystyle \left( \frac{\pi}{2} \right) ~$ がある場合は、ロルの定理の前提条件に不適のため、ロルの定理は使えません。
$~f(x)=|x|(a=-2,b=2)~$ の場合
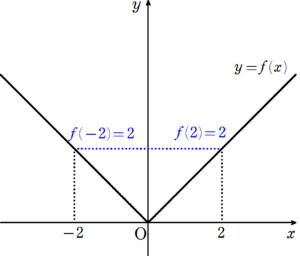
図6からわかる通り、$~f'(c)=0~$ となるような $~c \in (0,\pi)~$ は存在しない。
適用範囲に微分不可能な点( $~0~$ )がある場合も、ロルの定理の前提条件に不適のため、ロルの定理は使えません。
以上の2つの例からもわかる通り、連続や微分可能という条件がいかに大切かがわかりました。
ロルの定理の証明
ロルの定理の意味を理解したところで、どんな時でも成り立つかを証明してみましょう。
グラフの形を、$~f(a)~$との比較で場合分けをする。
(1) $~f(a)~$ よりも大きくなる点が存在するとき
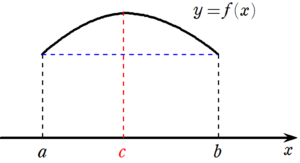
グラフの形は図7のようになり、最大値の原理から$~x \in(a,b)~$ で最大値 $~f(c)(c \in (a,b) )~$ が存在する。
$~c~$ で微分可能であるため、 $~f'(c)~$ を考えると、$~b~$ 側からの接線の傾きは右下がり($~0~$以下)なので
f'(c)=\displaystyle \lim_{h \to +0}\frac{f(c+h)-f(c)}{h} \le 0 ~~~\cdots①となる。
また、 $~a~$ 側から接線の傾きは右上がり($~0~$以上)なので
f'(c)=\displaystyle \lim_{h \to -0}\frac{f(c+h)-f(c)}{h} \ge 0~~~\cdots②となる。
$①$と$②$より、
f'(c)= 0
が求まる。
(2) $~f(a)~$ よりも小さくなる点が存在するとき
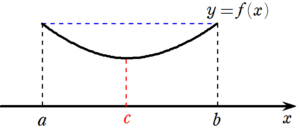
グラフの形は図8のようになり、最小値の原理から$~x \in(a,b)~$ で最小値 $~f(c)(c \in (a,b) )~$ が存在する。
(1)と同様に考えて、 $~b~$ 側からの接線の傾きは右上がり($~0~$以上)なので
f'(c)=\displaystyle \lim_{h \to +0}\frac{f(c+h)-f(c)}{h} \ge 0 ~~~\cdots③となり、 $~a~$ 側から接線の傾きは右下がり($~0~$以下)なので
f'(c)=\displaystyle \lim_{h \to -0}\frac{f(c+h)-f(c)}{h} \le 0 ~~~\cdots④となるため、$③$と$④$より、
f'(c)= 0
が求まる。
(3) $~f(x)=t(一定)~$ のとき
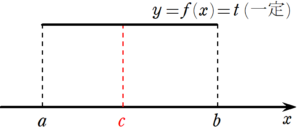
$~f(a)~$ よりも大きくなる点や小さくなる点が存在しないとき、グラフの形は図9のように一定となる。
$~x\in(a,b)~$ で、 $~f'(x)=t’=0~$ となるため、
f'(c)= 0
である。
(1)~(3)より、題意は示された。 $~\blacksquare $
ロルの定理の例2にように、(1)と(2)を組み合わせたパターンもあり、その場合は$~f^{\prime}(c)=0~$となる$~c~$が複数存在するだけの違いです。
ロルの定理を利用すれば、平均値の定理も証明できます。


図で考えると簡単だね。



視覚化って数学では大切。
参考文献
- 高木貞治(2010)『定本 解析概論』,p.51,岩波書店.
- Bertrand Hauchecorne , Daniel Suratteau(2015)『世界数学者事典』,p671,熊原啓作訳,日本評論社.

コメント