私学適性（数学）平成31年度解説　大問２

他の年度については、コチラからどうぞ。

　サイトのデザイン変更中に伴い、このページは多少見づらくなっています。
　解説の内容自体に影響はありません。

---

問題集にも載っていますが、解答だけをまずは示します。
問題番号をクリックすると、各問題の解説にスクロールします。

---

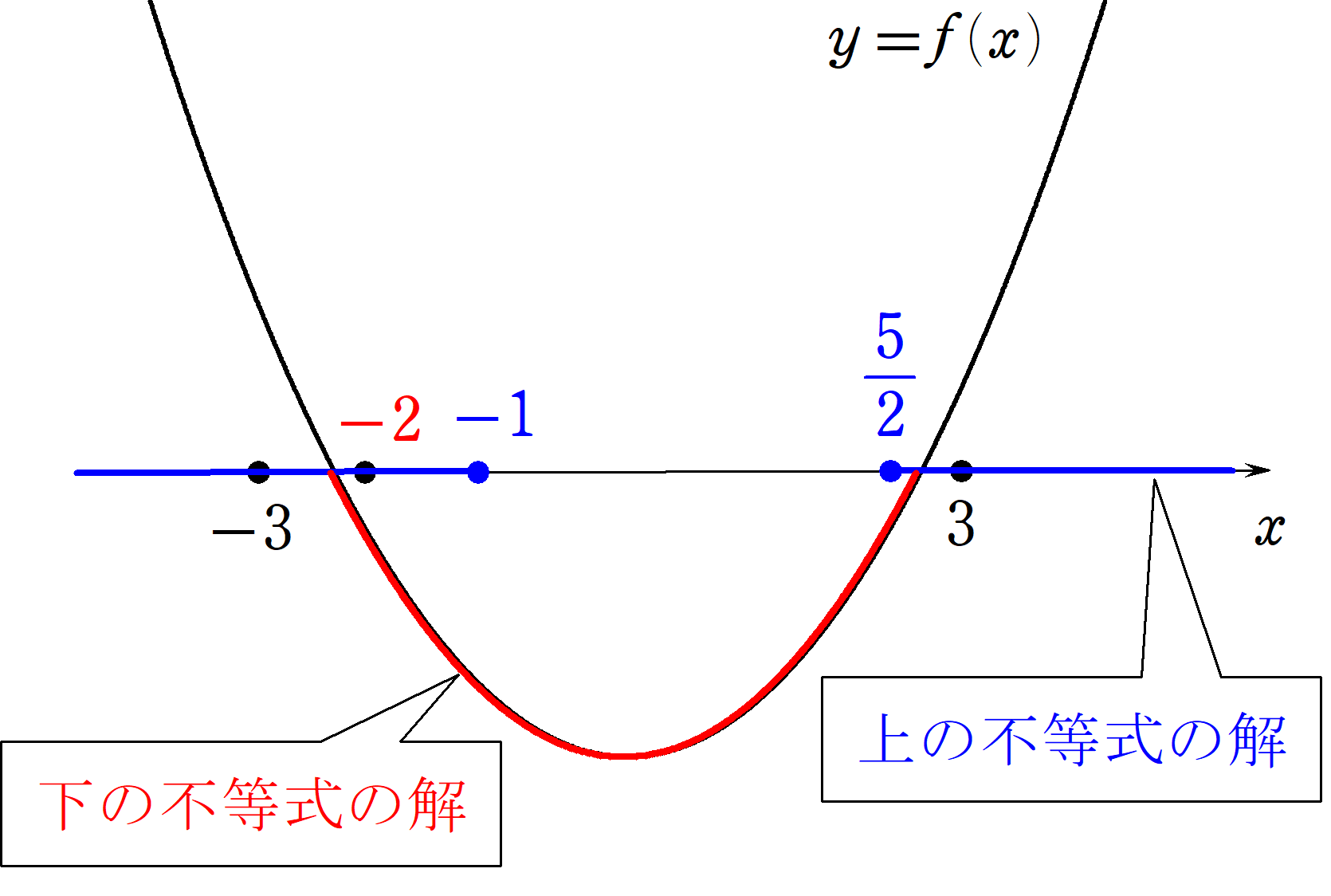
２(1)

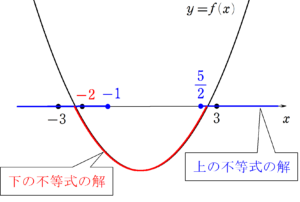
まず、上の不等式を解くと、
\begin{align}
2x^2-3x-5 &> 0 \\
(x+1)(2x-5) &> 0 \\
x < -1,\displaystyle \frac{5}{2} &< x
\end{align}
であるため、連立不等式をみたす整数 $~x~$ の個数が１つになる場合は、 $~x=-2~$ か $~x=3~$ に限られる。
 
\begin{equation}
f(x)=x^2+(a-3)x-2a+2
\end{equation}
とおき、各場合における $~f(x)~$ のグラフの形を考える。
 
 
$~x=-2~$ のとき
$~y=f(x)~$ のグラフは、次のような形になる。

① $~x=-3~$ が含まれないようにするため、 $~f(-3) \ge 0~$ （元の不等式が $~f(x)$$<$ $~0~$ であることに注意。）
これにより、
\begin{align}
(-3)^2-3(a-3)-2a+2 &\ge 0 \\
9-3a+9-2a+2 &\ge 0 \\
-5a &\ge -20 \\
a &\le 4 \cdots ①
\end{align}
が求まる。
 
② $~x=-2~$ は解にならないといけないため、 $~f(-2) < 0~$ 。これにより、
\begin{align}
(-2)^2-2(a-3)-2a+2 &< 0 \\
4-2a+6-2a+2 &< 0 \\
-4a &< -12 \\
a &> 3 \cdots ②
\end{align}
が求まる。
 
③ $~x=3~$ が含まれないようにするため、 $~f(3) \ge 0~$ （元の不等式が $~f(x)$$<$ $~0~$ であることに注意。）
これにより、
\begin{align}
3^2+3(a-3)-2a+2 &\ge 0 \\
9-3a-9-2a+2 &\ge 0 \\
-5a &\ge -2 \\
a &\le \displaystyle \frac{2}{5} \cdots ③
\end{align}
が求まる。
 
①～③より、 $~3 < a \le 4~$ が求まる。
 
 
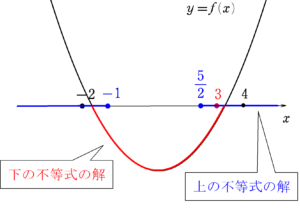
$~x=3~$ のとき
$~y=f(x)~$ のグラフは、次のような形になる。

④ $~x=-2~$ が含まれないようにするため、 $~f(-2) \ge 0~$ （元の不等式が $~f(x)$$<$ $~0~$ であることに注意。）
これにより、
\begin{align}
(-2)^2-2(a-3)-2a+2 &\ge 0 \\
4-2a+6-2a+2 &\ge 0 \\
-4a &\ge -12 \\
a &\le 3 \cdots ④
\end{align}
が求まる。
 
⑤ $~x=3~$ は解にならないといけないため、 $~f(3) < 0~$ 。これにより、
\begin{align}
3^2+3(a-3)-2a+2 &< 0 \\
9+3a-9-2a+2 &< 0 \\
a &< -2 \cdots ⑤
\end{align}
が求まる。
 
⑥ $~x=4~$ が含まれないようにするため、 $~f(4) \ge 0~$ （元の不等式が $~f(x)$$<$ $~0~$ であることに注意。）
これにより、
\begin{align}
4^2+4(a-3)-2a+2 &\ge 0 \\
16+4a-12-2a+2 &\ge 0 \\
2a &\ge -6 \\
a &\ge -3\cdots ⑥
\end{align}
が求まる。
 
④～⑥より、 $~3 \le a < -2~$ が求まるが、問題文で $~a \ge 0~$ とあるため、不適。
 
 
以上より、 $~3 < a \le 4~$ が求まった。

---

２(2)

$~2^x+2^{-x}=X~$ とおく。この両辺を２乗すると、
\begin{align}
(2^x+2^{-x})^2&=X^2 \\
4^x+4^{-x}+2\cdot 2^x \cdot 2^{-x}&=X^2 \\
4^x+4^{-x}+2&=X^2 \\
4^x+4^{-x}&=X^2-2 \\
\end{align}
となるので、元の式は、
\begin{align}
y&=X^2-2-5X-3 \\
&=X^2-5X-5
\end{align}
と $~X~$ で表せて、平方完成をすると、
\begin{align}
&=\displaystyle \left( X-\frac{5}{2} \right)^2 -\frac{25}{4}-5 \\
&=\left( X-\frac{5}{2} \right)^2 -\frac{45}{4} \cdots(*)
\end{align}
である。
 
$~X~$ の変域は、相加相乗平均より、
\begin{equation}
X \ge 2\sqrt{2^x \cdot 2^{-x}}=2
\end{equation}
なので、 $~(*)~$ より、 $~y~$ の最小値は $~\displaystyle -\frac{45}{4}~$ であることが求まった。
 
 
また、このとき $~X=\displaystyle \frac{5}{2}~$ なので、
\begin{equation}
2^x+2^{-x}=\displaystyle \frac{5}{2}
\end{equation}
を解けば、 $~x~$ の値も求まる。
 
$~2^x=t~$ とおくと、
\begin{align}
\displaystyle t+\frac{1}{t}&=\frac{5}{2} \\
\\
2t^2+2&=5t \\
2t^t-5t+2&=0 \\
(2t-1)(t-2)&=0 \\
\\
t&=\frac{1}{2},2
\end{align}
と求まり、 $~t~$ をもどすと、
\begin{align}
\displaystyle 2^x=\frac{1}{2}&,2^x=2 \\
x=-1&,x=1
\end{align}
となるので、 $~y~$ が最小値をとるとき、 $~x=\pm 1~$ と求まった。

---

２(3)

①

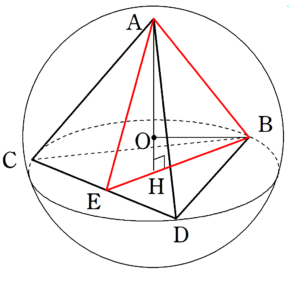
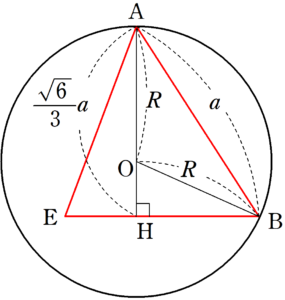
上の図で考える。この正四面体 $~ABCD~$ を、三点 $~A,B,E~$ で切断すると、下の図のようになる。

正四面体の１辺の長さが $~a~$ のとき、正四面体の高さ $~AH=\displaystyle \frac{\sqrt{6}}{3}a~$ となる（→「正四面体の高さと体積」を参照）ので、 $~\triangle ABH~$ で三平方の定理を使うと、
\begin{align}
BH^2&=AB^2-AH^2 \\
\\
&=\displaystyle a^2-\left( \frac{\sqrt{6}}{3}a \right)^2 \\
\\
&=a^2-\frac{6}{9}a^2 \\
\\
&=\frac{1}{3}a^2 \cdots(*)
\end{align}
となる。
 
また、外接球の半径を $~R~$ とすると、 $~\triangle OBH~$ で三平方の定理から、
\begin{align}
BH^2&=OB^2-OH^2 \\
\\
&=\displaystyle R^2-\left( \frac{\sqrt{6}}{3}a-R \right)^2 \\
\\
&=R^2-\left( \frac{6}{9}a^2-\frac{2\sqrt{6}}{3}aR+R^2 \right) \\
\\
&=R^2-\frac{2}{3}a^2+\frac{2\sqrt{6}}{3}aR-R^2 \\
&=-\frac{2}{3}a^2+\frac{2\sqrt{6}}{3}aR \cdots(**)
\end{align}
となる。
 
$~a > 0~$ に注意しながら、 $~(*)=(**)~$ を式変形していくと、
\begin{align}
\displaystyle \frac{1}{3}a^2&=-\frac{2}{3}a^2+\frac{2\sqrt{6}}{3}aR \\
\\
-\frac{2\sqrt{6}}{3}aR &=-a^2 \\
\\
-\frac{2\sqrt{6}}{3}R &=-a \\
\\
R&=\frac{3}{2\sqrt{6}}a \\
\\
R&=\frac{\sqrt{6}}{4}a
\end{align}
が求まった。

---

②

正四面体の１辺の長さが $~a~$ のとき、正四面体の体積は、
\begin{equation}
V=\displaystyle \frac{\sqrt{2}}{12}a^3\cdots(ⅰ)
\end{equation}
となる。（→「正四面体の高さと体積」を参照）
 
また、内接球の半径 $~r~$ を使うと、正四面体の体積は、
\begin{equation}
V=\displaystyle \frac{r}{3}\cdot (各面の面積の和）
\end{equation}
で表せるため、１辺 $~a~$ の正三角形の面積が $~\displaystyle \frac{\sqrt{3}}{4}a^2~$ である（→「正n角形の面積」を参照）ことを用いると、
\begin{align}
V&=\displaystyle \frac{r}{3} \cdot \left( \frac{\sqrt{3}}{4}a^2 \cdot 4 \right) \\
\\
&=\frac{r}{3} \cdot \sqrt{3}a^2 \\
\\
&=\frac{\sqrt{3}}{3}a^2 r \cdots(ⅱ)
\end{align}
となる。
 
$~a > 0~$ に注意しながら、 $~(ⅰ)=(ⅱ)~$ を式変形していくと、
\begin{align}
\displaystyle \frac{\sqrt{2}}{12}a^3&=\frac{\sqrt{3}}{3}a^2 r \\
\\
\sqrt{2}a^3&=4\sqrt{3}a^2 r \\
\\
4\sqrt{3}a^2 r&=\sqrt{2}a^3 \\
\\
r&=\frac{\sqrt{2}}{4\sqrt{3}}a \\
\\
r&=\frac{\sqrt{6}}{12}a
\end{align}
が求まった。

---

２(4)

まず、２倍角の公式を使って式変形をしていくと、
\begin{align}
\displaystyle \sin{2\theta}&=\frac{2}{r^2} \\
\\
2\sin{\theta}\cos{\theta}\cdot r^2&=2 \\
\\
\sin{\theta}\cos{\theta}\cdot r^2&=1 \\
\\
r\sin{\theta} \cdot r\cos{\theta}&=1 \\
\end{align}
となる。
 
ここで $~r\cos{\theta}=x,r\sin{\theta}=y~$ を代入すると、
\begin{align}
y\cdot x&=1 \\
\\
\displaystyle y&=\frac{1}{x}
\end{align}
が求まった。

---

２(5)

①

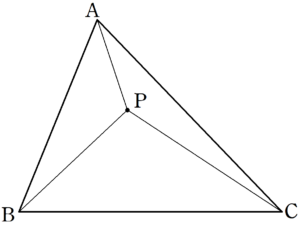
上図より、
\begin{equation}
\overrightarrow{BP}=\overrightarrow{AP}-\overrightarrow{AB},\overrightarrow{CP}=\overrightarrow{AP}-\overrightarrow{AC}
\end{equation}
であるため、与式に代入して、

\begin{align}
\displaystyle 3\overrightarrow{AP}+4(\overrightarrow{AP}-\overrightarrow{AB})+5(\overrightarrow{AP}-\overrightarrow{AC})&=\bar{0} \\
\\
3\overrightarrow{AP}+4\overrightarrow{AP}-4\overrightarrow{AB}+5\overrightarrow{AP}-5\overrightarrow{AC}&=\bar{0} \\
\\
12\overrightarrow{AP}&=4\overrightarrow{AB}+5\overrightarrow{AC} \\
\\
\overrightarrow{AP}&=\frac{1}{3}\overrightarrow{AB}+\frac{5}{12}\overrightarrow{AC}
\end{align}

\begin{align}
\displaystyle 3\overrightarrow{AP}+4(\overrightarrow{AP}-\overrightarrow{AB})+5(\overrightarrow{AP}-\overrightarrow{AC})&=\bar{0} \\
\\
3\overrightarrow{AP}+4\overrightarrow{AP}-4\overrightarrow{AB}+5\overrightarrow{AP}-5\overrightarrow{AC}&=\bar{0} \\
\\
\\
12\overrightarrow{AP}=4\overrightarrow{AB}+5\overrightarrow{AC}& \\
\\
\overrightarrow{AP}=\frac{1}{3}\overrightarrow{AB}+\frac{5}{12}\overrightarrow{AC}&
\end{align}

が求まった。

---

②

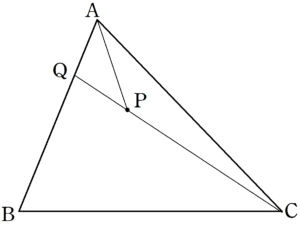
$~\triangle AQC~$ に注目すると、 $~P~$ は辺 $~QC~$ 上にあるため、
\begin{equation}
\overrightarrow{AP}=t\overrightarrow{AQ}+(1-t)\overrightarrow{AC}(0 < t < 1)
\end{equation}
と表せる。この式に $~\overrightarrow{AQ}=k\overrightarrow{AB}~$ を代入すれば、
\begin{equation}
\overrightarrow{AP}=kt\overrightarrow{AB}+(1-t)\overrightarrow{AC}
\end{equation}
となる。
 
上式と、①の係数を比較することで、
\begin{cases}
kt=\displaystyle \frac{1}{3} & \cdots (ⅰ) \\
\\
1-t=\frac{5}{12} &\cdots(ⅱ) \\
\end{cases}
であり、(ⅱ)より、 $~\displaystyle t=\frac{7}{12}~$ 。これを(ⅰ)に代入して、
\begin{align}
\displaystyle \frac{7}{12}k&=\frac{1}{3} \\
\\
k&=\frac{4}{7}
\end{align}
が求まった。

---

２(6)

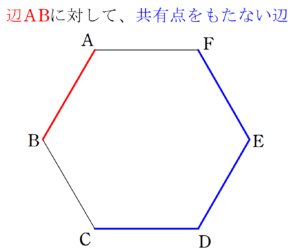
選んだ２本の線分について、次の３つに場合分けをして考える。
 
①辺と辺の組み合わせの場合

重複に気を付けて、各組合せを考えると、

辺 $~AB~$ に対し、共有店を持たないのは $~CD,DE,EF~$ 。
辺 $~BC~$ に対し、共有店を持たないのは $~DE,EF,FA~$ 。
辺 $~CD~$ に対し、共有店を持たないのは $~EF,FA~$ 。
辺 $~DE~$ に対し、共有店を持たないのは $~FA~$ 。

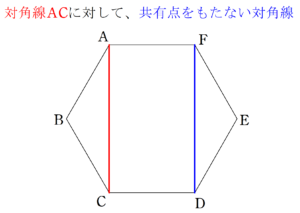
なので、９組。
 
②対角線と対角線の組み合わせの場合

重複に気を付けて、各組合せを考えると、

対角線 $~AC~$ と対角線 $~DF~$
対角線 $~BD~$ と対角線 $~EA~$
対角線 $~CE~$ と対角線 $~FB~$

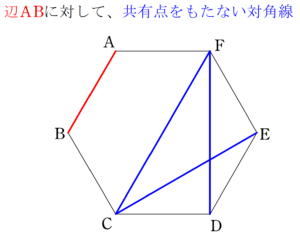
なので、３組。
 
③辺と対角線の組み合わせの場合

辺 $~AB~$ に対し、対角線 $~CE,DF,CF~$ の３組。

これを各辺について考えてあげればよいので、 $~3 \times 6=18~$ 組。
 
 
①～③を合計して、３０組である。

---

２(7)

集合 $~A~$ は、４で割って１余る整数（ $~1~$ を除く）の集合なので、
\begin{equation}
A=\{ 5,9,13,17,\cdots,191,193,197 \}
\end{equation}
であり、集合 $~B~$ は、６で割って１余る整数の集合なので、
\begin{equation}
B=\{ 1,7,13,19,\cdots,187,193,199 \}
\end{equation}
となる。
 
４で割って１余る整数は、１から２００までの中に $~50~$ 個あるが、 $~A~$ に１は含まれないので、 $~n(A)=49~$ 。
 
６で割って１余る整数は、１から２００までの中に $~34~$ 個。よって、 $~n(B)=34~$ 。
 
 
次に、 $~A~$ と $~B~$ の共通集合 $~A \cap B~$ を考える。
４で割っても６で割っても１余る整数、すなわち１２で割って１余る整数（ $~1~$ を除く）の集合なので、
\begin{equation}
A \cap B=\{ 13,25,37,49,\cdots,169,181,193 \}
\end{equation}
となる。
 
１２で割って１余る整数は、１から２００までの中に $~17~$ 個あるが、 $~A \cap B~$ に１は含まれないので、 $~n(A \cap B)=16~$ 。
 
以上より、
\begin{align}
n(A \cup B)&=n(A)+n(B)-n(A \cap B) \\
&=49+34-16 \\
&=67
\end{align}
となるため、 $~A \cup B~$ の要素の個数が求まった。

---

２(8)

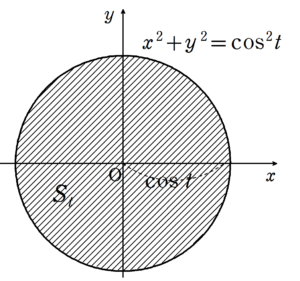
平面 $~z=t~$ で切断すると、次のような図形になる。

つまり、$S_t~$ は円なので、この面積を $~0~$ から $~\displaystyle \frac{\pi}{2}~$ まで積分すると、
\begin{align}
\displaystyle &\int_{0}^{\frac{\pi}{2}}\pi \cos^2{t}dt \\
\\
&=\pi \int_{0}^{\frac{\pi}{2}} \frac{\cos{2t}}{2}+\frac{1}{2}dt \\
\\
&=\pi \left[ \frac{\sin{2t}}{4}+\frac{1}{2}t \right]_{0}^{\frac{\pi}{2}} \\
\\
&=\pi \cdot \frac{\pi}{4} \\
\\
&=\frac{\pi^2}{4}
\end{align}
となるため、立体の体積は求まった。

---

２(9)

$~4 \le x < y < z~$ より、逆数をとると、
\begin{equation}
\displaystyle \frac{1}{4} \ge \frac{1}{x} > \frac{1}{y} > \frac{1}{z} \cdots ①
\end{equation}
となる。
 
①を使って、与式を変形すると、
\begin{align}
\displaystyle \frac{1}{2}&=\frac{1}{x}+\frac{1}{y}+\frac{1}{z} \\
\\
&< \frac{1}{x}+\frac{1}{x}+\frac{1}{x} \\
\\
&=\frac{3}{x}
\end{align}
となり、すなわち
\begin{align}
\displaystyle \frac{1}{2} &< \frac{3}{x} \\
\\
x &< 6 \\
\end{align}
である。これにより、 $~x=4,5~$ と求まった。
 
 
$~x=4~$ のとき
与式は
\begin{align}
\displaystyle \frac{1}{4}+\frac{1}{y}+\frac{1}{z} &=\frac{1}{2} \\
\\
\frac{1}{y}+\frac{1}{z} &=\frac{1}{4} \cdots ② \\
\end{align}
となる。ここに①の式を使うと、
\begin{align}
\displaystyle \frac{1}{4}&=\frac{1}{y}+\frac{1}{z} \\
\\
&< \frac{1}{y}+\frac{1}{y} \\
\\
&=\frac{2}{y}
\end{align}
となり、すなわち
\begin{align}
\displaystyle \frac{1}{4}&< \frac{2}{y} \\
\\
y &< 8
\end{align}
である。 $~4=x < y~$ より、 $~y=5,6,7~$ と求まった。
 
$~x=4~$ で、 $~y=5~$ のとき、
②に代入して、
\begin{align}
\displaystyle \frac{1}{5}+\frac{1}{z}&=\frac{1}{4} \\
\\
\frac{1}{z}&=\frac{1}{20} \\
\\
z&=20
\end{align}
が求まった。
 
$~x=4~$ で、 $~y=6~$ のとき、
②に代入して、
\begin{align}
\displaystyle \frac{1}{6}+\frac{1}{z}&=\frac{1}{4} \\
\\
\frac{1}{z}&=\frac{1}{12} \\
\\
z&=12
\end{align}
が求まった。
 
$~x=4~$ で、 $~y=7~$ のとき、
②に代入して、
\begin{align}
\displaystyle \frac{1}{7}+\frac{1}{z}&=\frac{1}{4} \\
\\
\frac{1}{z}&=\frac{3}{28} \\
\\
z&=\frac{28}{3}
\end{align}
が求まるが、 $~z~$ は自然数でないので不適。
 
 
$~x=5~$ のとき
与式は
\begin{align}
\displaystyle \frac{1}{5}+\frac{1}{y}+\frac{1}{z} &=\frac{1}{2} \\
\\
\frac{1}{y}+\frac{1}{z} &=\frac{3}{10} \cdots ③ \\
\end{align}
となる。ここに①の式を使うと、
\begin{align}
\displaystyle \frac{3}{10}&=\frac{1}{y}+\frac{1}{z} \\
\\
&< \frac{1}{y}+\frac{1}{y} \\
\\
&=\frac{2}{y}
\end{align}
となり、すなわち
\begin{align}
\displaystyle \frac{3}{10}&< \frac{2}{y} \\
\\
3y &< 20 \\
\\
y &< \frac{20}{3} \fallingdotseq 6.7
\end{align}
である。 $~5=x < y~$ より、 $~y=6~$ と求まった。
 
$~x=5~$ で、 $~y=6~$ のとき、
③に代入して、
\begin{align}
\displaystyle \frac{1}{6}+\frac{1}{z}&=\frac{3}{10} \\
\\
\frac{1}{z}&=\frac{2}{15} \\
\\
z&=\frac{15}{2}
\end{align}
が求まるが、 $~z~$ は自然数でないので不適。
 
 
以上より、 $~(x,y,z)=(4,5,20),(4,6,12)~$ と求まった。

---

２(10)

①

$~f”(x)~$ の両辺を $~x~$ で積分すると、
\begin{align}
\displaystyle f'(x)&=\int -\cos{x}dx \\
\\
&=-\sin{x}+C_1 (C_1は積分定数）
\end{align}
となる。
 
次に、 $~f'(x)~$ の両辺を $~x~$ で積分すると、
\begin{align}
\displaystyle f(x)&=\int -\sin{x}+C_1 dx \\
\\
&=\cos{x}+C_1x+C_2 (C_2は積分定数）
\end{align}
となる。
 
$~f(0)=5~$ より、
\begin{align}
\cos{0}+C_1 \cdot 0+C_2&=5 \\
1+C_2&=5 \\
C_2&=4
\end{align}
が求まり、また $~f(\pi)=0~$ より、
\begin{align}
\cos{\pi}+C_1 \cdot \pi+4&=0 \\
-1+\pi C_1+4&=0 \\
\pi C_1&=-3 \\
\\
C_1&=-\displaystyle \frac{3}{\pi}
\end{align}
が求まるため、元の $~f(x)~$ に代入して、
\begin{equation}
\displaystyle f(x)=\cos{x}-\frac{3}{\pi}x+4
\end{equation}
が求まった。

---

②

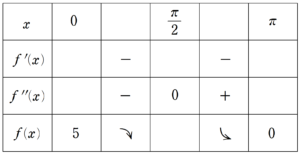
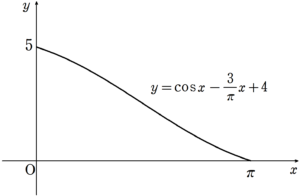
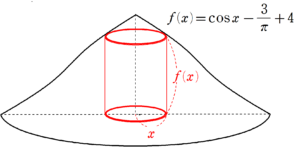
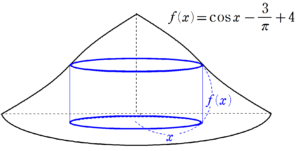
問題文や①で求まった $~f(x)~$ の情報を、増減表で整理すると次のようになる。

増減表をもとに、グラフの概形を書くと、次のようになる。

このグラフを $~y~$ 軸の周りに１回転させてできる立体の体積を、下のような半径 $~x~$ 円柱によって、円周×高さを横に重ねていくように積分する。


すなわち、
\begin{align}
&\displaystyle \int_{0}^{\pi} 2\pi x \cdot f(x)dx \\
\\
&=2\pi \int_{0}^{\pi} x\left( \cos{x}-\frac{3}{\pi}x+4 \right)dx \\
\\
&=2\pi \int_{0}^{\pi} x \cos{x}-\frac{3}{\pi}x^2+4x dx \\
\end{align}
を求めればよい。
 
 
各項の積分は、
\begin{align}
&\displaystyle \int_{0}^{\pi} x\cos{x} dx \\
\\
&=\left[ x\sin{x} \right]_{0}^{\pi} – \int_{0}^{\pi} \sin{x}dx \\
\\
&=0-\left[ -\cos{x} \right]_{0}^{\pi} \\
\\
&=-(1+1) \\
\\
&=-2
\end{align}
\begin{align}
&\displaystyle \int_{0}^{\pi} -\frac{3}{\pi}x^2 dx \\
\\
&=\left[ -\frac{1}{\pi}x^3 \right]_{0}^{\pi} \\
\\
&=-\pi^2
\end{align}
\begin{align}
&\displaystyle \int_{0}^{\pi} 4x dx \\
\\
&=\left[ 2x^2 \right]_{0}^{\pi} \\
\\
&=2\pi^2
\end{align}
となるので、求めたい積分は、
\begin{align}
&\displaystyle 2\pi \left( -2- \pi^2+2\pi^2 \right) \\
&=2\pi \left( -2+\pi^2 \right) \\
&=2\pi^3-4\pi
\end{align}
と求まった。

---

---

◇参考文献等
・『私学教員適性検査問題集　数学（平成29年度～31年度）』