イングランドの数学者ジョン・ウォリス(John Wallis)が、1656年に主著の中で発表した公式です。ある規則で並んだ分数を無限にかけていくと円周率が登場するため、微積分学を用いた円周率の近似値計算の先駆けにもなりました。
①ウォリスの公式
②証明
③円周率の近似計算
①ウォリスの公式
\begin{equation}
\displaystyle \prod_{n=1}^{\infty}\frac{(2n)^2}{(2n-1)(2n+1)}=\frac{\pi}{2}
\end{equation}
左辺は、
\begin{equation}
\displaystyle \frac{(2n)^2}{(2n-1)(2n+1)}
\end{equation}
という式を、 $~n=1~$ のときから、 $~n~$ が無限大になるまでずっと”かける”という意味です。
つまり、
\begin{equation}
\displaystyle \frac{2^2}{1 \times 3} \times \frac{4^2}{3 \times 5} \times \frac{6^2}{5 \times 7} \times \cdots
\end{equation}
というような意味です。これを無限回行うと、円周率 $~\pi~$ の値の半分になるなんて不思議ですね。そのカラクリを次章で証明していきます。
②証明
はさみうちの原理を使って、左辺の収束値を求めようという方法です。
自然数 $~n~$ に対して、
\begin{equation}
\displaystyle I_{n}=\int_{0}^{\frac{\pi}{2}} \sin^{n}x dx
\end{equation}
とおく。(この積分をウォリス積分という)
$\displaystyle 0\lex\le\frac{\pi}{2} ~$ では、$ 0\le\sin{
x}\le1 ~$ となるため、
\begin{align}
0 \le \sin^{2n+2}x \le \sin^{2n+1}x \le \sin^{2n}x
\end{align}
となり、積分をとって、
\begin{align}
\displaystyle 0 < \int_{0}^{\frac{\pi}{2}} \sin^{2n+2}x dx < \int_{0}^{\frac{\pi}{2}} \sin^{2n+1}x dx < \int_{0}^{\frac{\pi}{2}} \sin^{2n}x dx
\end{align}
である。つまり、
\begin{align}
0< I_{2n+2} < I_{2n+1} < I_{2n}
\end{align}
となる。ここで、 $~I_{n}~$ を部分積分していくことを考えると、
\begin{align}
\displaystyle I_{n}&=\int_{0}^{\frac{\pi}{2}} \sin^{n}x dx \\
&=\int_{0}^{\frac{\pi}{2}} \sin^{n-1}x \cdot \sin{x} dx \\
&=\int_{0}^{\frac{\pi}{2}} \sin^{n-1}x \cdot (-\cos{x})’ dx \\
&=\left[ -\sin^{n-1}x \cdot \cos{x} \right]_{0}^{\frac{\pi}{2}} + \int_{0}^{\frac{\pi}{2}} (n-1) \sin^{n-2}x \cdot \cos^{2}x dx \\
&=(n-1) \int_{0}^{\frac{\pi}{2}} \sin^{n-2}x (1-\sin^{2}x) dx \\
&=(n-1) \int_{0}^{\frac{\pi}{2}} \sin^{n-2}x dx -(n-1) \int_{0}^{\frac{\pi}{2}} \sin^{n}x dx \\
&=(n-1)I_{n-2}-(n-1)I_{n}
\end{align}
つまり、
\begin{align}
\displaystyle I_{n}&=(n-1)I_{n-2}-(n-1)I_{n} \\
\\
I_{n}&=(n-1)I_{n-2}-n I_{n}+I_{n} \\
\\
n I_{n}&=(n-1)I_{n-2} \\
\\
I_{n}&=\frac{n-1}{n}I_{n-2}
\end{align}
という関係が導ける。
この関係式から、
\begin{align}
\displaystyle I_{2n}&=\frac{2n-1}{2n}I_{2n-2} \\
\\
&=\frac{2n-1}{2n} \cdot \frac{2n-3}{2n-2}I_{2n-4} \\
\\
&\vdots \\
\\
&=\frac{2n-1}{2n} \cdot \frac{2n-3}{2n-2} \cdot \cdots \cdot \frac{3}{4} \cdot \frac{1}{2}\cdots I_{0} \\
\\
&=\frac{(2n-1)!!}{(2n)!!}I_{0}
\end{align}
と変形できる。( $~(n)!!~$ は二重階乗といい、 $~n~$ から2ずつ減らしていく階乗。)
ここで、
\begin{align}
\displaystyle I_{0}&=\int_{0}^{\frac{\pi}{2}} \sin^{0}x dx \\
&=\int_{0}^{\frac{\pi}{2}} dx \\
&= \left[x \right]_{0}^{\frac{\pi}{2}}\\
\\
&=\frac{\pi}{2}
\end{align}
であるため、
\begin{equation}
\displaystyle I_{2n}=\frac{(2n-1)!!}{(2n)!!} \cdot \frac{\pi}{2}
\end{equation}
となる。この式に $~n=n+1~$ を代入することで、
\begin{equation}
\displaystyle I_{2n+2}=\frac{(2n+1)!!}{(2n+2)!!} \cdot \frac{\pi}{2}
\end{equation}
も得られる。
また、
\begin{align}
\displaystyle I_{2n+1}&=\frac{2n}{2n+1}I_{2n-1} \\
\\
&=\frac{2n}{2n+1} \cdot \frac{2n-2}{2n-1}I_{2n-3} \\
\\
&\vdots \\
\\
&=\frac{(2n)!!}{(2n+1)!!} \cdot I_{1} \\
\end{align}
となり、
\begin{align}
\displaystyle I_{1}&=\int_{0}^{\frac{\pi}{2}} \sin{x} dx \\
&= \left[-\cos{x} \right]_{0}^{\frac{\pi}{2}}\\
\\
&=1
\end{align}
であるため、
\begin{equation}
\displaystyle I_{2n+1}=\frac{(2n)!!}{(2n+1)!!}
\end{equation}
が得られる。
これまでに得られた $~I_{2n} , I_{2n+1} , I_{2n+2} ~$ を、元の不等式に代入すると、
\begin{equation}
\displaystyle \frac{(2n+1)!!}{(2n+2)!!} \cdot \frac{\pi}{2}< \frac{(2n)!!}{(2n+1)!!}< \frac{(2n-1)!!}{(2n)!!} \cdot \frac{\pi}{2}
\end{equation}
となる。各辺 $~\displaystyle \frac{(2n-1)!!}{(2n)!!}~$ でわると、
\begin{equation}
\displaystyle \frac{(2n+1)}{(2n+2)} \cdot \frac{\pi}{2}< \frac{\frac{2n}{2n-1}\cdot \frac{2n-2}{2n-3}\cdots \frac{2}{1}}{\frac{2n+1}{2n}\cdot \frac{2n-1}{2n-2} \cdots \frac{3}{2}} < \frac{\pi}{2}
\end{equation}
これを変形していくことで、
\begin{equation}
\displaystyle \frac{(2n+1)}{(2n+2)} \cdot \frac{\pi}{2}< \frac{(2n)^2}{(2n+1)(2n-1)}\cdot \frac{(2n-2)^2}{(2n-1)(2n-3)} \cdot \cdots \cdot \frac{2^2}{3\cdot 1}< \frac{\pi}{2}
\end{equation}
\begin{equation}
\displaystyle \frac{(2n+1)}{(2n+2)} \cdot \frac{\pi}{2}< \prod_{k=1}^{n}\frac{(2k)^2}{(2k-1)(2k+1)} < \frac{\pi}{2}
\end{equation}
となる。ここで、 $~n\to \infty~$ とすると、 $~\displaystyle \frac{(2n+1)}{(2n+2)} \cdot \frac{\pi}{2} \to \frac{\pi}{2}~$ なので、はさみうちの原理より、
\begin{equation}
\displaystyle \prod_{n=1}^{\infty}\frac{(2n)^2}{(2n-1)(2n+1)}=\frac{\pi}{2}
\end{equation}
となり、ウォリスの公式は示された。 $~\blacksquare$
自然数 $~n~$ に対して、
\begin{equation}
\displaystyle I_{n}=\int_{0}^{\frac{\pi}{2}} \sin^{n}x dx
\end{equation}
とおく。(この積分をウォリス積分という)
$\displaystyle 0\lex\le\frac{\pi}{2} ~$ では、$ 0\le\sin{
x}\le1 ~$ となるため、
\begin{align}
0 \le \sin^{2n+2}x \le \sin^{2n+1}x \le \sin^{2n}x
\end{align}
となり、積分をとって、
\begin{multline}
\displaystyle 0 < \int_{0}^{\frac{\pi}{2}} \sin^{2n+2}x dx < \int_{0}^{\frac{\pi}{2}} \sin^{2n+1}x dx \\
< \int_{0}^{\frac{\pi}{2}} \sin^{2n}x dx
\end{multline}
である。つまり、
\begin{align}
0< I_{2n+2} < I_{2n+1} < I_{2n}
\end{align}
となる。ここで、 $~I_{n}~$ を部分積分していくことを考えると、
\begin{align}
\displaystyle I_{n}&=\int_{0}^{\frac{\pi}{2}} \sin^{n}x dx \\
&=\int_{0}^{\frac{\pi}{2}} \sin^{n-1}x \cdot \sin{x} dx \\
&=\int_{0}^{\frac{\pi}{2}} \sin^{n-1}x \cdot (-\cos{x})' dx \\
&=\left[ -\sin^{n-1}x \cdot \cos{x} \right]_{0}^{\frac{\pi}{2}} \\
&+ \int_{0}^{\frac{\pi}{2}} (n-1) \sin^{n-2}x \cdot \cos^{2}x dx \\
&=(n-1) \int_{0}^{\frac{\pi}{2}} \sin^{n-2}x (1-\sin^{2}x) dx \\
&=(n-1) \int_{0}^{\frac{\pi}{2}} \sin^{n-2}x dx \\
&-(n-1) \int_{0}^{\frac{\pi}{2}} \sin^{n}x dx \\
&=(n-1)I_{n-2}-(n-1)I_{n}
\end{align}
つまり、
\begin{align}
\displaystyle I_{n}&=(n-1)I_{n-2}-(n-1)I_{n} \\
\\
I_{n}&=(n-1)I_{n-2}-n I_{n}+I_{n} \\
\\
n I_{n}&=(n-1)I_{n-2} \\
\\
I_{n}&=\frac{n-1}{n}I_{n-2}
\end{align}
という関係が導ける。
この関係式から、
\begin{align}
\displaystyle I_{2n}&=\frac{2n-1}{2n}I_{2n-2} \\
\\
&=\frac{2n-1}{2n} \cdot \frac{2n-3}{2n-2}I_{2n-4} \\
\\
&\vdots \\
\\
&=\frac{2n-1}{2n} \cdot \frac{2n-3}{2n-2} \cdot \cdots \cdot \frac{3}{4} \cdot \frac{1}{2}\cdots I_{0} \\
\\
&=\frac{(2n-1)!!}{(2n)!!}I_{0}
\end{align}
と変形できる。( $~(n)!!~$ は二重階乗といい、 $~n~$ から2ずつ減らしていく階乗。)
ここで、
\begin{align}
\displaystyle I_{0}&=\int_{0}^{\frac{\pi}{2}} \sin^{0}x dx \\
&=\int_{0}^{\frac{\pi}{2}} dx \\
&= \left[x \right]_{0}^{\frac{\pi}{2}}\\
\\
&=\frac{\pi}{2}
\end{align}
であるため、
\begin{equation}
\displaystyle I_{2n}=\frac{(2n-1)!!}{(2n)!!} \cdot \frac{\pi}{2}
\end{equation}
となる。この式に $~n=n+1~$ を代入することで、
\begin{equation}
\displaystyle I_{2n+2}=\frac{(2n+1)!!}{(2n+2)!!} \cdot \frac{\pi}{2}
\end{equation}
も得られる。
また、
\begin{align}
\displaystyle I_{2n+1}&=\frac{2n}{2n+1}I_{2n-1} \\
\\
&=\frac{2n}{2n+1} \cdot \frac{2n-2}{2n-1}I_{2n-3} \\
\\
&\vdots \\
\\
&=\frac{(2n)!!}{(2n+1)!!} \cdot I_{1} \\
\end{align}
となり、
\begin{align}
\displaystyle I_{1}&=\int_{0}^{\frac{\pi}{2}} \sin{x} dx \\
&= \left[-\cos{x} \right]_{0}^{\frac{\pi}{2}}\\
\\
&=1
\end{align}
であるため、
\begin{equation}
\displaystyle I_{2n+1}=\frac{(2n)!!}{(2n+1)!!}
\end{equation}
が得られる。
これまでに得られた $~I_{2n} , I_{2n+1} , I_{2n+2} ~$ を、元の不等式に代入すると、
\begin{equation}
\displaystyle \frac{(2n+1)!!}{(2n+2)!!} \cdot \frac{\pi}{2}< \frac{(2n)!!}{(2n+1)!!}< \frac{(2n-1)!!}{(2n)!!} \cdot \frac{\pi}{2}
\end{equation}
となる。各辺 $~\displaystyle \frac{(2n-1)!!}{(2n)!!}~$ でわると、
\begin{equation}
\displaystyle \frac{(2n+1)}{(2n+2)} \cdot \frac{\pi}{2}< \frac{\frac{2n}{2n-1}\cdot \frac{2n-2}{2n-3}\cdots \frac{2}{1}}{\frac{2n+1}{2n}\cdot \frac{2n-1}{2n-2} \cdots \frac{3}{2}} < \frac{\pi}{2}
\end{equation}
これを変形していくことで、
\begin{multline}
\displaystyle \frac{(2n+1)}{(2n+2)} \cdot \frac{\pi}{2} \\
< \frac{(2n)^2}{(2n+1)(2n-1)}\cdot \cdots \cdot \frac{2^2}{3\cdot 1}< \frac{\pi}{2}
\end{multline}
\begin{equation}
\displaystyle \frac{(2n+1)}{(2n+2)} \cdot \frac{\pi}{2}< \prod_{k=1}^{n}\frac{(2k)^2}{(2k-1)(2k+1)} < \frac{\pi}{2}
\end{equation}
となる。ここで、 $~n\to \infty~$ とすると、 $~\displaystyle \frac{(2n+1)}{(2n+2)} \cdot \frac{\pi}{2} \to \frac{\pi}{2}~$ なので、はさみうちの原理より、
\begin{equation}
\displaystyle \prod_{n=1}^{\infty}\frac{(2n)^2}{(2n-1)(2n+1)}=\frac{\pi}{2}
\end{equation}
となり、ウォリスの公式は示された。 $~\blacksquare$
はさみうちの原理をうま~く使った方法でした。二重階乗まで登場して少し計算が面倒ですね。
③円周率の近似計算
ウォリスの公式は、左辺は整数分数の積(永遠に)、右辺は円周率の半分であるため、左辺を無限に計算することで、円周率の値を求めることができます。
では、どれくらいの精度なのでしょうか?計算してみました。
円周率$\pi~$ は、ウォリスの公式を変形して次のように表せる。
\begin{equation}
\displaystyle \pi=2\cdot \lim_{n \to \infty}\prod_{k=1}^{n}\frac{(2k)^2}{(2k-1)(2k+1)}
\end{equation}
この式はウォリスの公式を $~\pi~$ について解き、右辺を少し変形したものです。 $~n~$ を1ずつ増やして、 $~\pi~$ の値を求めてみます。
\begin{align}
\pi&=2\cdot \frac{2^2}{1\cdot 3} \\
&=2 \cdot \frac{4}{3} \\
&=2.66666666666
\end{align}
$~n=1~$ の誤差は0.47492598
円周率のカケラのありません。
\begin{align}
\pi&=2\cdot \frac{2^2}{1\cdot 3}\times \frac{4^2}{3\cdot 5}\\
&=2\cdot \frac{64}{45} \\
&=2.8222222222
\end{align}
$~n=2~$ の誤差は0.29714820
まだまだです。
$~n=3,4~$ のときも $~\pi<3~$ でした・・。
\begin{align}
\pi&=2\cdot \frac{2^2}{1\cdot 3}\times \frac{4^2}{3\cdot 5}\cdots \frac{10^2}{9\cdot 11}\\
&=3.002176
\end{align}
$~n=5~$ の誤差は0.13941669
やっと、3がでてきました。
次は3.1を目指します・・・。武器は電卓からエクセルに・・・。
\begin{align}
\pi&=2\cdot \frac{2^2}{1\cdot 3}\times \frac{4^2}{3\cdot 5}\cdots \frac{38^2}{37\cdot 39}\\
&=3.101577
\end{align}
$~n=19~$ の誤差は0.0400153
これで3.1です。
よし、次は3.14・・・。
\begin{align}
\pi&=2\cdot \frac{2^2}{1\cdot 3}\times \frac{4^2}{3\cdot 5}\cdots \frac{986^2}{985\cdot 987}\\
&=3.14000157
\end{align}
$~n=493~$ の誤差は0.00159108
有名な3.14がやっと出てきました。
思い切って1000までやってみましょう。
\begin{align}
\pi&=2\cdot \frac{2^2}{1\cdot 3}\times \frac{4^2}{3\cdot 5}\cdots \frac{2000^2}{1999\cdot 2001}\\
&=3.14080774
\end{align}
$~n=1000~$ の誤差は0.00078490
う~ん。収束速度が遅い・・。
最後の最後に $~n=10000~$ まで計算してみました。
\begin{align}
\pi&=2\cdot \frac{2^2}{1\cdot 3}\times \frac{4^2}{3\cdot 5}\cdots \frac{20000^2}{19999\cdot 20001}\\
&=3.14151411
\end{align}
$~n=10000~$ の誤差は0.00007853
エクセル様おつかれさまでした(> <)
ということで、非常に $~\pi~$ の値を近似するには手間のかかる公式であることがわかりました。
電卓のない時代には厳しいです。
最後に $~n~$ を増やしていったときの様子をグラフにしたものを載せておきます。
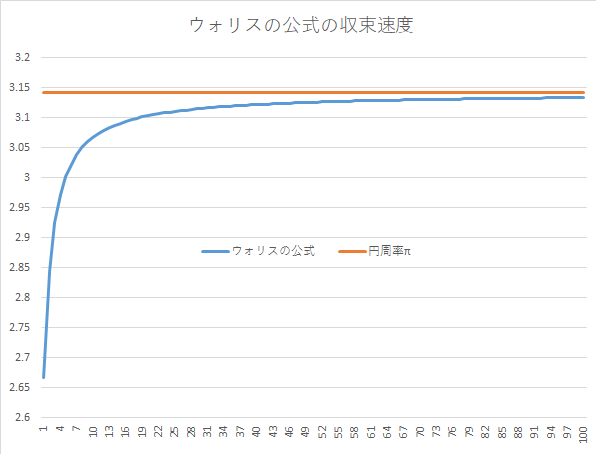
ウォリスの公式、割とシンプルに円周率が表されていると思いきや、円周率本来の値に収束するまでに非常に時間がかかる(> <)。ただ、証明をする際に部分積分を使うので、難関大学を狙う高校生への問題として適していると思いました。(実際、ウォリスの公式を利用した入試問題も多く出ているようです。)

☆参考文献等
・中村力(2016)『数学検定1級準拠テキスト 微分積分』,pp.66-67,森北出版.
・「Wikipedia ジョン・ウォリス」,<https://ja.wikipedia.org/wiki/%E3%82%B8%E3%83%A7%E3%83%B3%E3%83%BB%E3%82%A6%E3%82%A9%E3%83%AA%E3%82%B9 > 2017年3月20日アクセス
コメント