ブレートシュナイダーの公式〜2通りの証明方法や歴史を解説！

2025年9月15日

当ページのリンクには広告が含まれています。

　ブレートシュナイダーの公式は、四角形の4つの辺の長さと対角の和がわかっているときに使える面積公式です。

S = \sqrt{(s-a)(s-b)(s-c)(s-d) - abcd\cos^2\frac{\theta}{2}}

　ブレートシュナイダーの公式は、円に内接するという条件が必要なブラーマグプタの公式を一般化したもので、面積を求められる条件の範囲で言うと、次のような位置を占めています。

ヘロンの公式 \subset ブラーマグプタの公式 \subset ブレートシュナイダーの公式

　しかし、その一方で「使い道がほとんどない」とも言われるこの公式。一体なぜなのでしょうか？

　この記事では、ブレートシュナイダーの公式の使い方から証明、そしてその実用性までを、現役数学教員で、数学史の先生でもあるFukusukeが詳しく解説していきます。

この記事を書いた人

Fukusuke（ふくすけ）
数学史の先生

現役の中学・高校数学教員
著書2冊重刷、ブログ累計200万PV達成
行間がなくなるほど丁寧な式変形で執筆中

この記事を書いた人

Fukusuke（ふくすけ）
数学史の先生

現役の中学・高校数学教員
著書2冊は発売1ヶ月で即重刷
当数学史ブログは累計200万PV達成
行間がなくなるほど丁寧な式変形で記事を執筆

『世界を変えた数学史図鑑』『教養としての数学史』好評発売中！

この記事を読んでわかること

ブレートシュナイダーの公式とは？

どんな四角形の面積でも求められる

　ブレートシュナイダーの公式は、四角形の4辺の長さと、対角の和の半分を用いて、その面積を求める公式です。

ブレートシュナイダーの公式

　四角形$~ABCD~$において、$~AB = a~$、$~BC = b~$、$~CD = c~$、$~DA = d~$のとき、

\angle A + \angle C = \theta^{※},~ s = \frac{a+b+c+d}{2}

とおくと、四角形$~ABCD~$の面積を$~S~$は、次のように求まる。

S = \sqrt{(s-a)(s-b)(s-c)(s-d) - abcd\cos^2\frac{\theta}{2}}

$※~\angle B + \angle D = \theta~$としても一般性は失われない。

　この公式の最大の特徴は、円に内接するなどの特別な条件を必要とせず、あらゆる四角形に対して成り立つ点です。

　ブラーマグプタの公式が円に内接する四角形にしか使えないのに対し、ブレートシュナイダーの公式はその制約を取り払った一般的な公式と言えます。

使い道はほとんどない

　しかし、これほど強力な公式でありながら、実用的な場面でブレートシュナイダーの公式が使われることはほとんどありません。

　その理由は、公式を使うために「2つの対角の角度」が必要になる点にあります。

　実際の測量などでも、四角形の面積を求める際4辺の長さを測ることは比較的簡単ですが、対角の角度まで正確に測定するのは困難です。（古代ローマの測量では、四角形を分割して三角形2つにしてヘロンの公式を使っていました）

　また、そもそも4辺の長さだけでは四角形の形は一意に定まりません。

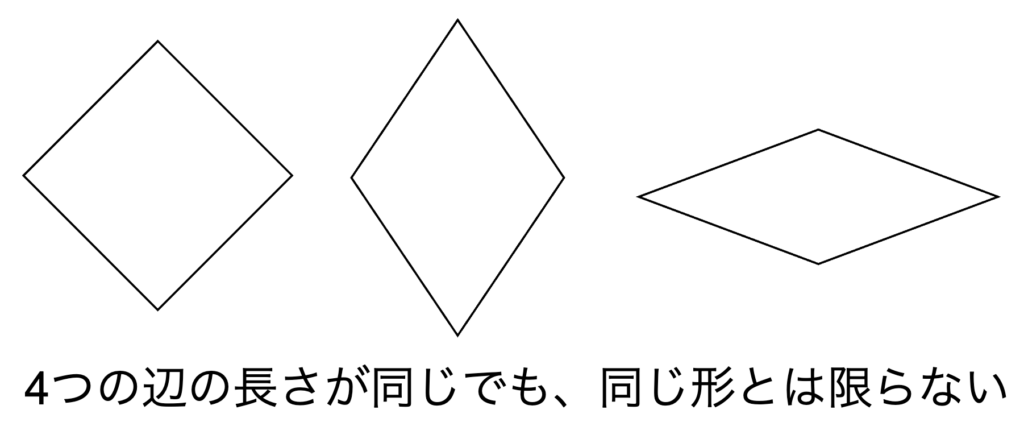
　このような理由から、ブレートシュナイダーの公式は理論的な価値は高いものの、実用性は低いと言わざるを得ません。

　高校の数学でこの公式が登場することはほとんどなく、大学レベルの数学や数学史の中で触れられる程度です。

ブレートシュナイダーはドイツの数学者

　この公式に名を残すカール・アントン・ブレートシュナイダー（Carl Anton Bretschneider ,1808~1878）は、19世紀に活躍したドイツの数学者です。

　1808年にゴータで生まれ、1878年に亡くなりました。

　彼は数学者であると同時にジュリスト（法学者）でもあり、幾何学や数論、数学史など幅広い分野で研究を行っていました。

　ブレートシュナイダーの公式は、彼の数ある業績の中でも特に有名で、彼の名を後世に伝えています。

ブレートシュナイダーの公式の2通りの証明

　ブレートシュナイダーの公式の証明は、余弦定理や三角関数の性質を巧みに利用します。

脇役の角から証明する方法

　まずは多くのサイトにも載っている一般的な方法から。

ブレートシュナイダーの公式の証明1

　四角形$~ABCD~$を対角線$~AC~$で区切る。

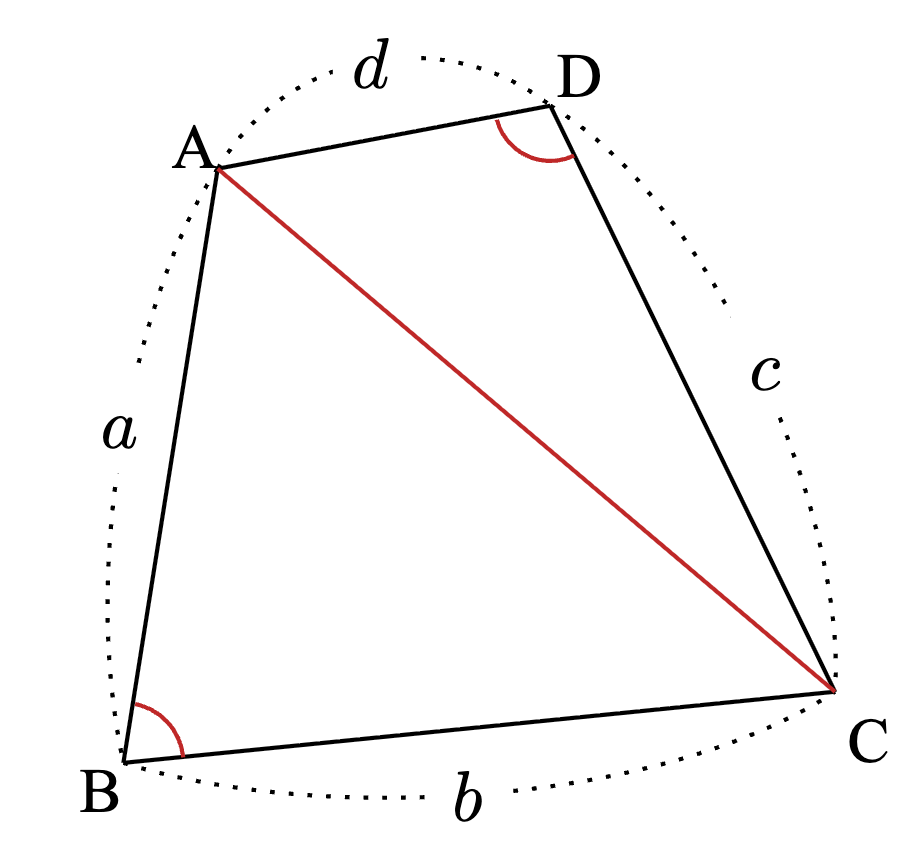
　このとき、

\triangle ABC = \frac{1}{2}ab\sin{B}, ~ \triangle ADC = \frac{1}{2}cd\sin{D}

なので、

\begin{align*} S &= \triangle ABC + \triangle ADC \\ &= \frac{1}{2}ab\sin{B} + \frac{1}{2}cd\sin{D} \end{align*}

と表せる。

　この両辺を2倍した後、2乗することで、

\begin{align*} 2S &= ab\sin{B} + cd\sin{D}\\ 4S^2 &= a^2b^2\sin^2{B} + 2abcd\sin{B}\sin{D} + c^2d^2\sin^2{D} \cdots ①\\ \end{align*}

が得られる。

　ここで、$~\triangle BAC~$で余弦定理を使うと、

AC^2 = a^2 + b^2 - 2ab\cos{B}

であり、$~\triangle DAC~$で余弦定理を使うと、

AC^2 = c^2 + d^2 - 2cd\cos{D}

なので、

\begin{align*} a^2 + b^2 - 2ab\cos{B} &= c^2 + d^2 - 2cd\cos{D}\\ a^2 + b^2 - c^2 - d^2 &= 2ab\cos{B} - 2cd\cos{D}\\ \frac{1}{2}(a^2 + b^2 - c^2 - d^2) &= ab\cos{B} - cd\cos{D}\\ \end{align*}

となり、両辺を2乗することで、

\frac{1}{4}(a^2 + b^2 - c^2 - d^2)^2 = a^2b^2\cos^2{B} - 2abcd\cos{B}\cos{D} + c^2d^2\cos^2{D} \cdots ②

が得られる。

　$~①+②~$の左辺は、

4S^2 + \frac{1}{4}(a^2+b^2-c^2-d^2)^2 \cdots ③

で、$~①+②~$の右辺は、

\begin{align*} &a^2b^2\sin^2{B} + 2abcd\sin{B}\sin{D} + c^2d^2\sin^2{D} + a^2b^2\cos^2{B} - 2abcd\cos{B}\cos{D} + c^2d^2\cos^2{D} \\ &= a^2b^2(\sin^2{B} + \cos^2{B}) + c^2d^2(\sin^2{D} + \cos^2{D}) - 2abcd(\cos{B}\cos{D} - \sin{B}\sin{D}) \\ &= a^2b^2 + c^2d^2 - 2abcd\cos(B+D) \cdots ④ \end{align*}

となる。

　$~A + B + C + D = 2\pi~$ ($~360°~$) であることから、

B + D = 2\pi - (A + C) = 2\pi - \theta

で、三角関数の関係や2倍角の公式から、

\begin{align*} \cos(B+D) &= \cos(2\pi - \theta) \\ &= \cos(-\theta) \\ &= \cos{\theta} \\ \end{align*}

であり、2倍角の公式 $~\cos{2\alpha} = 2\cos^2{\alpha} – 1~$に、$~\alpha = \frac{\theta}{2}~$ を代入することで、

\cos{\theta} = 2\cos^2{\frac{\theta}{2}} - 1

となるため、

\cos(B+D)=2\cos^2{\frac{\theta}{2}} - 1~~~\cdots⑤

が求められた。

　$~⑤~$を$~④~$に代入し、$~①+②~$の右辺は、

\begin{align*} &a^2b^2 + c^2d^2 - 2abcd\left(2\cos^2{\frac{\theta}{2}} - 1\right) \\ &= a^2b^2 + 2abcd + c^2d^2 - 4abcd\cos^2{\frac{\theta}{2}} \\ &= (ab + cd)^2 - 4abcd\cos^2{\frac{\theta}{2}} \cdots ⑥ \end{align*}

と変形できる。

　$~③~$と$~⑥~$より、

\begin{align*} 4S^2 + \frac{1}{4}(a^2+b^2-c^2-d^2)^2 &= (ab+cd)^2 - 4abcd\cos^2{\frac{\theta}{2}}\\ 4S^2 + 4abcd\cos^2{\frac{\theta}{2}} &= (ab+cd)^2 - \frac{1}{4}(a^2+b^2-c^2-d^2)^2\\ S^2 + abcd\cos^2{\frac{\theta}{2}} &= \frac{4(ab+cd)^2-(a^2+b^2-c^2-d^2)^2}{16} \cdots ⑦\\ \end{align*}

であり、$~⑦~$の右辺を因数分解すると、

\begin{align*} &\frac{(2ab+2cd)^2-(a^2+b^2-c^2-d^2)^2}{16}\\ &= \frac{\{2ab+2cd+(a^2+b^2-c^2-d^2)\}\{2ab+2cd-(a^2+b^2-c^2-d^2)\}}{16}\\ &= \frac{\{a^2+2ab+b^2-(c^2-2cd+d^2)\}\{c^2+2cd+d^2-(a^2-2ab+b^2)\}}{16}\\ &= \frac{\{(a+b)^2-(c-d)^2\}\{(c+d)^2-(a-b)^2\}}{16}\\ &= \frac{(a+b+c-d)\{a+b-(c-d)\}(c+d+a-b)\{(c+d)-(a-b)\}}{16}\\ &= \frac{(-a+b+c+d)(a-b+c+d)(a+b-c+d)(a+b+c-d)}{16}\\ &= \left(\frac{a+b+c+d}{2}-a\right)\left(\frac{a+b+c+d}{2}-b\right)\left(\frac{a+b+c+d}{2}-c\right)\left(\frac{a+b+c+d}{2}-d\right)\\ &= (s-a)(s-b)(s-c)(s-d) \cdots ⑧ \end{align*}

　なので、$~⑧~$を$~⑦~$に代入して、

\begin{align*} S^2 + abcd\cos^2{\frac{\theta}{2}} &= (s-a)(s-b)(s-c)(s-d)\\ S^2 &= (s-a)(s-b)(s-c)(s-d) - abcd\cos^2{\frac{\theta}{2}}\\ S &= \sqrt{(s-a)(s-b)(s-c)(s-d) - abcd\cos^2{\frac{\theta}{2}}}\\ \end{align*}

が求まった。$~\blacksquare~$

　証明の過程はやや複雑ですが、高校数学Ⅱまでの知識で十分に理解可能な方法でした。

主役の角から証明する方法

　途中までは上記の方法と似ているものの、こちらは半角の平方を利用してブレートシュナイダーの公式を作っていく方法です。

ブレートシュナイダーの公式の証明2

　四角形$~ABCD~$を対角線$~BD~$で区切る。

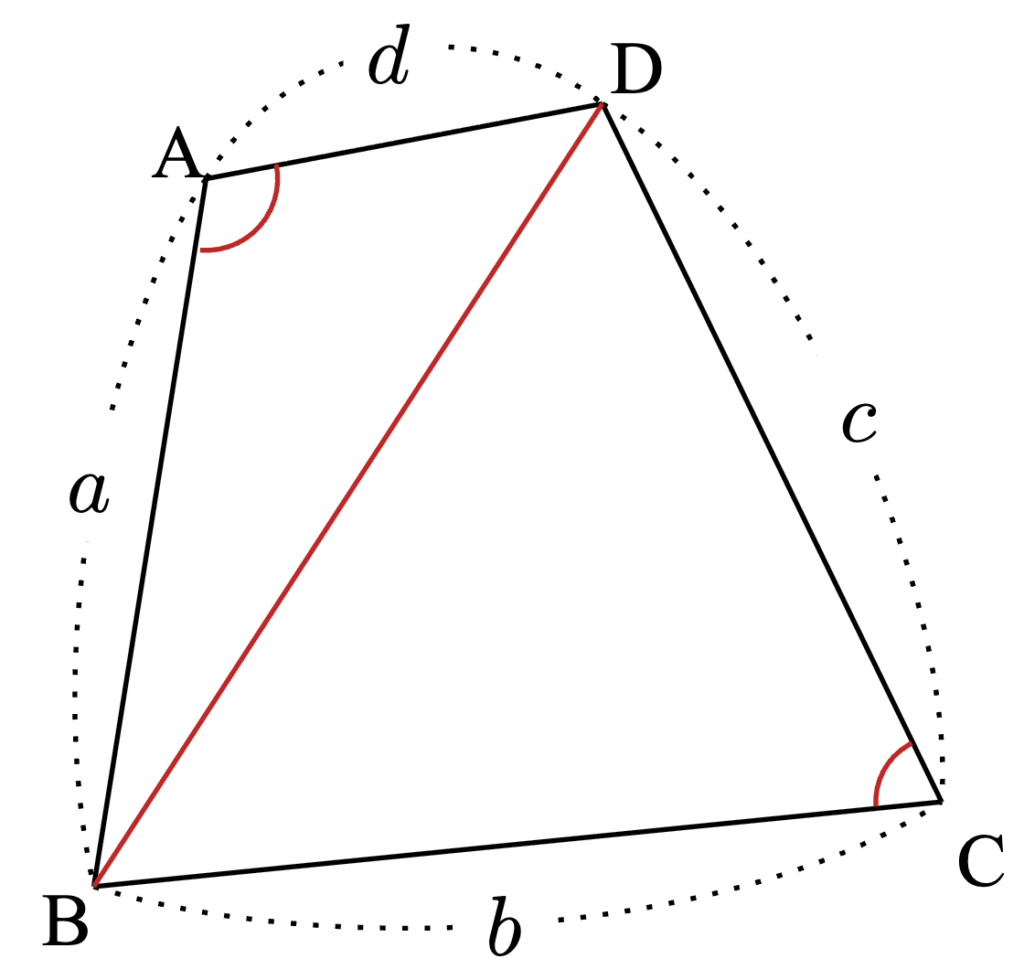
　$~\triangle ABD~$で余弦定理を使うと、

BD^2 = a^2 + d^2 - 2ad\cos{A}

であり、$~\triangle CBD~$で余弦定理を使うと、

BD^2 = b^2 + c^2 - 2bc\cos{C}

なので、

\begin{align*} a^2 + d^2 - 2ad\cos{A} &= b^2 + c^2 - 2bc\cos{C} \\ -2ad\cos{A} &= -a^2 - d^2 + b^2 + c^2 - 2bc\cos{C} \\ \cos{A} &= \frac{a^2 + d^2 - b^2 - c^2 + 2bc\cos{C}}{2ad} \cdots ⑨ \end{align*}

　半角の公式に$~⑨~$を代入することで、

\begin{align*} \cos^2{\frac{A}{2}} &= \frac{1}{2} + \frac{1}{2}\cos{A} \\ &= \frac{1}{2} + \frac{1}{2} \cdot \frac{a^2+d^2-b^2-c^2+2bc\cos{C}}{2ad} \\ &= \frac{2ad + a^2+d^2-b^2-c^2+2bc\cos{C}}{4ad} \end{align*}

　ここで、2倍角の公式 $~\cos{2\alpha} = 1 – 2\sin^2{\alpha}~$ に、$~\alpha = \frac{C}{2}~$ を代入すると、

\cos{C} = 1 - 2\sin^2{\frac{C}{2}}

なので、

\begin{align*} \cos^2{\frac{A}{2}} &= \frac{2ad+a^2+d^2-b^2-c^2+2bc\left(1-2\sin^2{\frac{C}{2}}\right)}{4ad} \\ &= \frac{a^2+2ad+d^2-b^2+2bc-c^2-4bc\sin^2{\frac{C}{2}}}{4ad} \\ &= \frac{(a+d)^2-(b-c)^2-4bc\sin^2{\frac{C}{2}}}{4ad} \\ &= \frac{(a+d)^2-(b-c)^2}{4ad} - \frac{bc\sin^2{\frac{C}{2}}}{ad} \\ &= \frac{\{(a+d)+(b-c)\}\{(a+d)-(b-c)\}}{4ad} - \frac{bc\sin^2{\frac{C}{2}}}{ad} \\ &= \frac{1}{ad} \cdot \frac{a+b-c+d}{2} \cdot \frac{a-b+c+d}{2} - \frac{bc\sin^2{\frac{C}{2}}}{ad} \\ &= \frac{1}{ad}\left(\frac{a+b+c+d}{2}-c\right)\left(\frac{a+b+c+d}{2}-b\right) - \frac{bc\sin^2{\frac{C}{2}}}{ad} \\ &= \frac{(s-c)(s-b) - bc\sin^2{\frac{C}{2}}}{ad} \end{align*}

となり、この両辺に$~ad~$をかけて移項することで、

\begin{align*} ad\cos^2{\frac{A}{2}} &= (s-c)(s-b) - bc\sin^2{\frac{C}{2}}\\ ad\cos^2{\frac{A}{2}} + bc\sin^2{\frac{C}{2}} &= (s-c)(s-b) \cdots ⑩\\ \end{align*}

が得られる。

同様に、

\begin{align*} \sin^2{\frac{A}{2}} &= \frac{1}{2} - \frac{1}{2}\cos{A} \\ &= \frac{1}{2} - \frac{1}{2} \cdot \frac{a^2+d^2-b^2-c^2+2bc\cos{C}}{2ad} \\ &= \frac{2ad - a^2-d^2+b^2+c^2-2bc\cos{C}}{4ad} \end{align*}

　ここで、2倍角の公式 $~\cos{2\alpha} = 2\cos^2{\alpha} – 1~$ に $~\alpha = \frac{C}{2}~$ を代入すると、

\cos{C} = 2\cos^2{\frac{C}{2}} - 1

なので、

\begin{align*} \sin^2{\frac{A}{2}} &= \frac{2ad - a^2-d^2+b^2+c^2-2bc\left(2\cos^2{\frac{C}{2}}-1\right)}{4ad} \\ &= \frac{-a^2+2ad-d^2+b^2+2bc+c^2-4bc\cos^2{\frac{C}{2}}}{4ad} \\ &= \frac{-(a-d)^2+(b+c)^2-4bc\cos^2{\frac{C}{2}}}{4ad} \\ &= \frac{(b+c)^2-(a-d)^2}{4ad} - \frac{bc\cos^2{\frac{C}{2}}}{ad} \\ &= \frac{\{(b+c)+(a-d)\}\{(b+c)-(a-d)\}}{4ad} - \frac{bc\cos^2{\frac{C}{2}}}{ad} \\ &= \frac{1}{ad} \cdot \frac{a+b+c-d}{2} \cdot \frac{-a+b+c+d}{2} - \frac{bc\cos^2{\frac{C}{2}}}{ad} \\ &= \frac{1}{ad}\left(\frac{a+b+c+d}{2}-d\right)\left(\frac{a+b+c+d}{2}-a\right) - \frac{bc\cos^2{\frac{C}{2}}}{ad} \\ &= \frac{(s-d)(s-a) - bc\cos^2{\frac{C}{2}}}{ad} \end{align*}

となり、この両辺に$~ad~$をかけて移項することで、

\begin{align*} ad\sin^2{\frac{A}{2}} &= (s-d)(s-a) - bc\cos^2{\frac{C}{2}}\\ ad\sin^2{\frac{A}{2}} + bc\cos^2{\frac{C}{2}} &= (s-d)(s-a) \cdots ⑪\\ \end{align*}

が得られる。

$~⑩×⑪~$を考えると、

(⑩\times⑪の左辺) = (s-a)(s-b)(s-c)(s-d) \cdots ⑫\\

\begin{align*} &~~~(⑩\times⑪の右辺) \\ &= \left(ad\cos^2{\frac{A}{2}} + bc\sin^2{\frac{C}{2}}\right)\left(ad\sin^2{\frac{A}{2}} + bc\cos^2{\frac{C}{2}}\right) \\ &= a^2d^2\sin^2{\frac{A}{2}}\cos^2{\frac{A}{2}} + b^2c^2\sin^2{\frac{C}{2}}\cos^2{\frac{C}{2}} + abcd\sin^2{\frac{A}{2}}\sin^2{\frac{C}{2}} + abcd\cos^2{\frac{A}{2}}\cos^2{\frac{C}{2}} \\ &= \left(ad\sin{\frac{A}{2}}\cos{\frac{A}{2}} + bc\sin{\frac{C}{2}}\cos{\frac{C}{2}}\right)^2 \\ &\quad~~~~~ - 2abcd\sin{\frac{A}{2}}\cos{\frac{A}{2}}\sin{\frac{C}{2}}\cos{\frac{C}{2}} + abcd\sin^2{\frac{A}{2}}\sin^2{\frac{C}{2}} + abcd\cos^2{\frac{A}{2}}\cos^2{\frac{C}{2}} \\ &= \left(ad\sin{\frac{A}{2}}\cos{\frac{A}{2}} + bc\sin{\frac{C}{2}}\cos{\frac{C}{2}}\right)^2 \\ &\quad~~~~~ + abcd\left(\cos^2{\frac{A}{2}}\cos^2{\frac{C}{2}} - 2\cos{\frac{A}{2}}\cos{\frac{C}{2}}\sin{\frac{A}{2}}\sin{\frac{C}{2}} + \sin^2{\frac{A}{2}}\sin^2{\frac{C}{2}}\right) \\ &= \left(ad\sin{\frac{A}{2}}\cos{\frac{A}{2}} + bc\sin{\frac{C}{2}}\cos{\frac{C}{2}}\right)^2 + abcd\left(\cos{\frac{A}{2}}\cos{\frac{C}{2}} - \sin{\frac{A}{2}}\sin{\frac{C}{2}}\right)^2 \cdots ⑬ \end{align*}

であり、2倍角の公式 $~2\sin{\alpha}\cos{\alpha} = \sin{2\alpha}~$ より、$~\sin{\alpha}\cos{\alpha} = \frac{1}{2}\sin{2\alpha}~$ なので、

\begin{align*} \left(ad\sin{\frac{A}{2}}\cos{\frac{A}{2}} + bc\sin{\frac{C}{2}}\cos{\frac{C}{2}}\right)^2 &= ad \cdot \frac{1}{2}\sin{A} + bc \cdot \frac{1}{2}\sin{C} \\ &= \frac{1}{2}ad\sin{A} + \frac{1}{2}bc\sin{C} \\ &= \triangle ABD + \triangle CBD \\ &= S \cdots ⑭ \end{align*}

となり、加法定理から、

\begin{align*} \left(\cos{\frac{A}{2}}\cos{\frac{C}{2}} - \sin{\frac{A}{2}}\sin{\frac{C}{2}}\right)^2 &= \left\{\cos\left(\frac{A}{2} + \frac{C}{2}\right)\right\}^2 \\ &= \cos^2{\frac{A+C}{2}} \\ &= \cos^2{\frac{\theta}{2}} \cdots ⑮ \end{align*}

　なので、$~⑫=⑬~$に$~⑭~$と$~⑮~$を代入して、

\begin{align*} S^2 + abcd\cos^2{\frac{\theta}{2}} &= (s-a)(s-b)(s-c)(s-d)\\ S^2 &= (s-a)(s-b)(s-c)(s-d) - abcd\cos^2{\frac{\theta}{2}}\\ S &= \sqrt{(s-a)(s-b)(s-c)(s-d) - abcd\cos^2{\frac{\theta}{2}}}\\ \end{align*}

とブレートシュナイダーの公式は求められた。$~\blacksquare~$

　個人的にはこちらの方がエレガントに感じます。
　この証明は以下のサイトを参考にさせていただきました。

まとめ

　ブレートシュナイダーの公式について、その使い方から証明、実用性までを解説しました。

どんな四角形でも面積が求められる一般化された公式
4辺の長さに加え、対角の角度の情報が必要となるため、実用性が低い
適用できる図形の範囲が、ヘロンの公式 ⊂ ブラーマグプタの公式 ⊂ ブレートシュナイダーの公式
19世紀ドイツの数学者ブレートシュナイダーによって発見された

　この公式は、数学の奥深さと、公式の背後にある理論の美しさを感じさせてくれる良い例と言えるでしょう。

$~d=0~$にすると、見事にヘロンの公式になるのがきれい！

名前も「ヘロン」→「ブラーマグプタ」→「ブレートシュナイダー」で、なんか強そうな感じだよね。

ブレートシュナイダーの公式〜2通りの証明方法や歴史を解説！