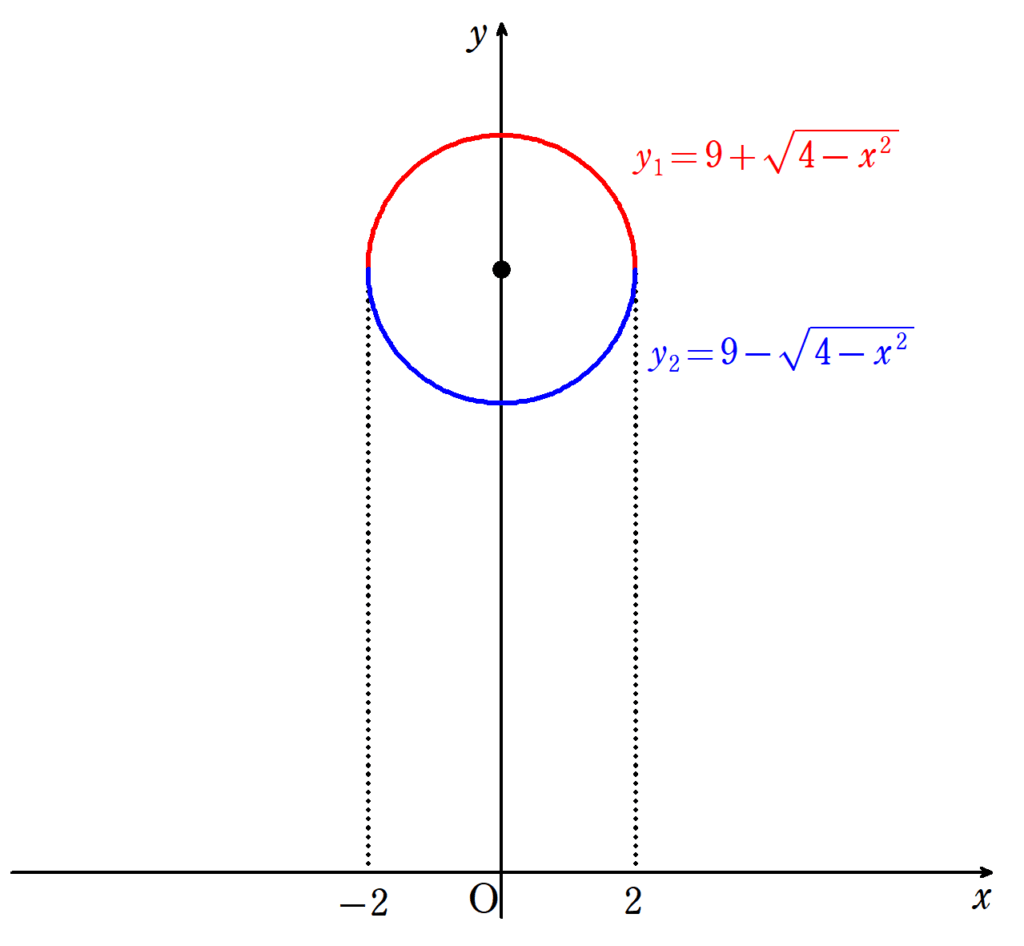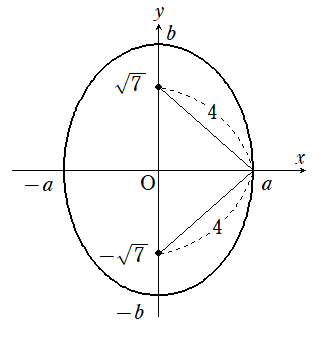大学専攻以上– tax –
-

2023はどんな数?素因数分解や約数、2023を含む数列を解説!
2023ってどんな数?2023は素数なの?という疑問に答えます!実は、2023は7や17で割りきれるため、素数ではありません。しかし、幸運数やハーシャッド数、ピタゴラス数にはあてはまっています。2023年の始まりにふさわしい、縁起の良さそうな式も紹介しているため、この記事を読むことで2023に親しみを持つことができます。 -

【数学史2-6】リンド・パピルスの有名問題を解説!方程式は仮置法で解ける!
古代エジプトの数学を知る上で、欠かせない資料が『リンド・パピルス』。「アハ問題」と呼ばれる方程式の問題やピラミッドの勾配の問題、等比数列の和の問題など、様々な分野の問題を扱っています。この記事では、その中でも有名な3つの問題を解説。今の数学でも使われたり、英語圏の童謡になっていたりと、現代にあらゆる形で残っています。 -

ギリシャの三大作図問題とは?各問題がギリシャに与えた影響まで解説!【数学史6-5】
三大作図問題として有名な「円積問題」「立方体倍積問題」「角の三等分問題」。19世紀に作図不可能と証明されるなど知る由もない古代ギリシャでは、数学者たちが問題に挑み、その過程で成果を上げました。また、当時は三大作図問題以外にも議論が盛んだった問題が3つ。古代ギリシャ発祥の合計6つの問題の歴史とその成果について解説します。 -

私学適性(数学)令和3年度解説 大問2
東京都私学教員適性検査の過去問(令和3年度)の答えを解説付きで載せています。問題集の解答例で、解法を調べたい際にご活用ください。大問1大問2(本ページ)※大... -

私学適性(数学)令和3年度解説 大問1
東京都私学教員適性検査の過去問(令和3年度)の答えを解説付きで載せています。問題集の解答例で、解法を調べたい際にご活用ください。大問1(本ページ)大問2※大... -

【数学史5-4】『九章算術』の連立方程式は歴史的にも高レベル!行列を使った解法を解説!
紀元前2世紀頃にでき、中国数学を体系立てた数学書である『九章算術』。その7,8章には、連立方程式の解法が載っており、解を仮定する「盈不足」と、行列の掃き出し法のもとになった「方程術」の2つが扱われていました。この記事では、それらの解き方を解説すると共に、『九章算術』に載っていた負の数の概念についても紹介します。 -

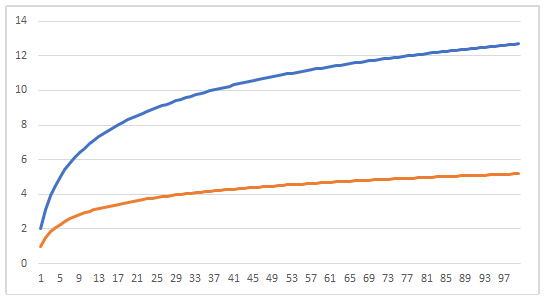
収束判定法:ダランベールからコーシーの証明
級数が収束するかどうかを判定するための方法として、「ダランベールの収束判定法」と「コーシーの収束判定法」があります。この2つの収束判定法の関係について考えま... -

コーシーの収束判定法
級数が収束するかどうかを計算から判定することができる方法です。いくつかの例はもちろん、なぜこの方法で判定できるのかを証明してみましょう。 【Ⅰ コーシーの収束... -

ダランベールの収束判定法
級数が収束するかどうかを計算から判定することができる方法です。いくつかの例はもちろん、なぜこの方法で判定できるのかを証明してみましょう。 【Ⅰ ダランベールの... -

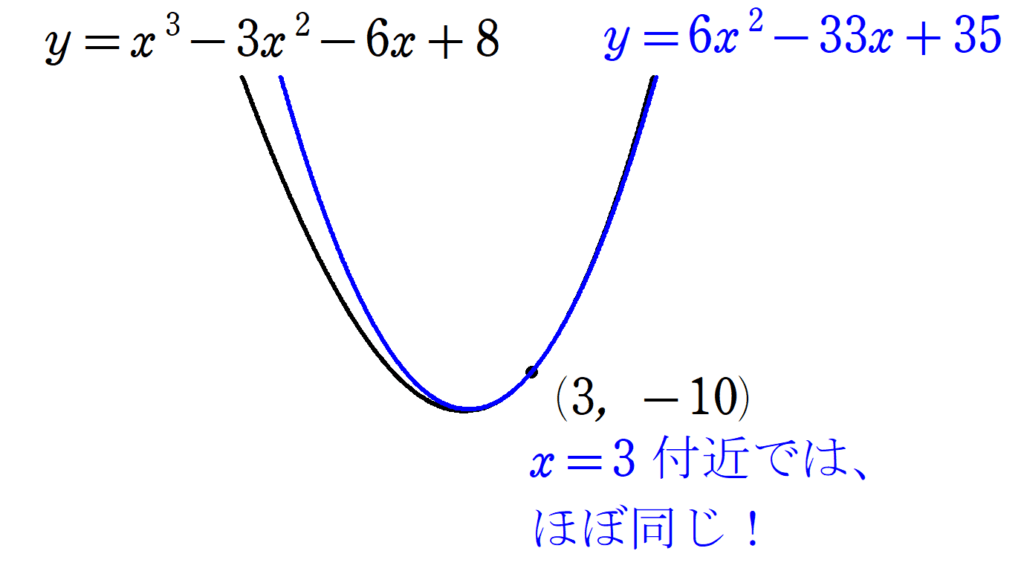
テイラーの定理~具体例からわかりやすく解説! 剰余項の由来はコーシーの平均値の定理!?~
解析学で非常に重要な「テイラー級数」。その基になっているのが「テイラーの定理」です。剰余項を含め、定理の内容を具体例からわかりやすく解説し、証明へと進みます。