数学ⅡB修了– tax –
-

立方体倍積問題を研究したアルキュタスはどんな数学者?発明家としての顔も解説!【数学史6-14】
アルキュタスは、古代ギリシャ時代に活躍した数学者、哲学者であり、動力を用いた機械仕掛けの鳥の発明で最もよく知られています。彼の数学への貢献、特に比例理論の発展は、後世の数学に大きな影響を与えました。本記事では、アルキュタスの思想、その革新的な発明、そして彼の業績が今日にどのように影響を与え続けているかを詳しく探ります。 -

数学者のヒポクラテスって何した人?ヒポクラテスの定理についても解説!【数学史6-10】
三日月図形の研究で有名な、古代ギリシャの数学者ヒポクラテス。円の面積と等しい正方形を作図する難問「円積問題」に取り組む中で、月形という曲線図形を直線図形に変形する術を思いつきました。この記事では、月形をはじめとするヒポクラテスの功績だけでなく、ヒポクラテスの不運なエピソードについてまで解説します。 -

三角錐数は三角数を重ねた数列!その一般項や美しい性質を解説!
この記事では、三角錐数に関する数学的概念を解説しています。三角数を基にした三角錐数の定義、それらの数の特徴、一般項の導出方法、そして奇数番目と偶数番目の三角錐数の異なる性質について紹介しています。また、パスカルの三角形と三角錐数の関連性にも触れられており、数学の興味深い側面を探求する内容となっています。 -

2024はどんな数字?素因数分解や約数、2024を含む数列を解説!
2024ってどんな数?2024は何で割れるの?という疑問に答えます!実は、2024は 2-0+2-4=0 より 11 の倍数です! また、2024は婚約数や三角錐数、ハーシャッド数であり、これらの数の性質についてわかりやすく解説しています。 -

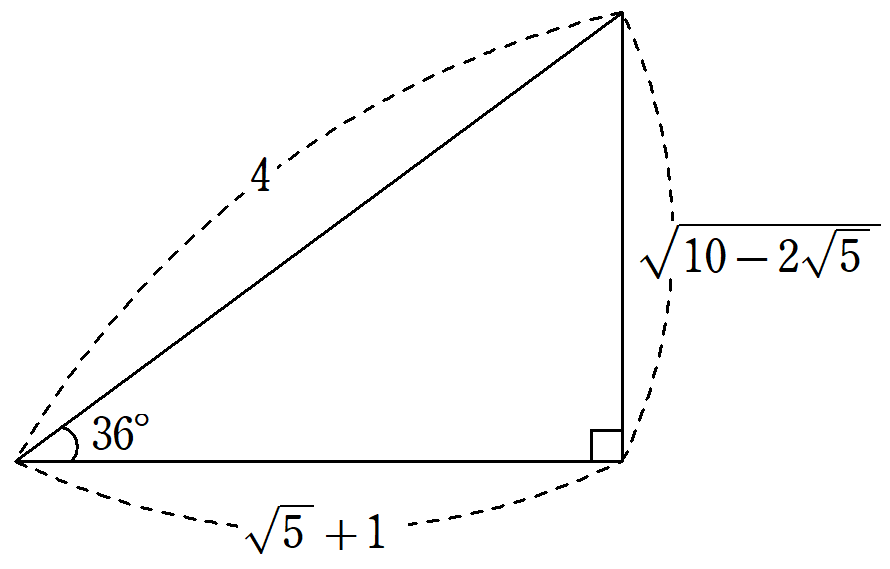
【まとめ】三角比の値~マイナーな角度の三角比まで表形式で紹介~
0°から90°までの三角比の値。数学Ⅰで学ぶのは0°、30°、45°、60°、90°の5つです。しかし、これらの角以外にも小数を使わずに正確な値を出せる角度があります。それらの値について、表形式でまとめました。リンク先の個別ページでは、値の出し方まで解説しています。 -

【数学史5-6】平方根は有限のみ対応!『九章算術』の開平法とは?
紀元前2世紀頃にでき、中国数学を体系立てた数学書である『九章算術』。その4章は、正方形の面積から一辺の長さを求める問題が載っており、図形を用いた開平算の方法が扱われていました。この記事では、その平方根を求める方法を中心に、4章「少広」の様々な問題について解説します。 -

【数学史3-8】バビロニアでは平方根の研究も?粘土板に残された√2の値とは?
三平方の定理や二次方程式を扱っていたバビロニア。当然必要となるのは平方根の知識であり、バビロニアの粘土板YBC7289から、√2の近似値が1.41421296 と求まっていたことがわかっています。ここまで緻密な値を求めるにあたって、利用されたのは相加相乗平均の考え方。その驚きの求め方をこの記事では解説します。 -

【数学史3-6】紀元前に二次方程式?バビロニアには解の公式が存在!
バビロニアでは、二次方程式 x²+px+q=0 を、p と q の符号によって場合分けしたうえで、それぞれ独自の方法で解いていました。しかも、それらの方法は「解の公式」や「解と係数の関係」に基づいています。バビロニアの粘土板に載っている、各場合における解き方を紹介すると同時に、それらの解き方が「解の公式」や「解と係数の関係」に繋がっている理由を解説します。 -

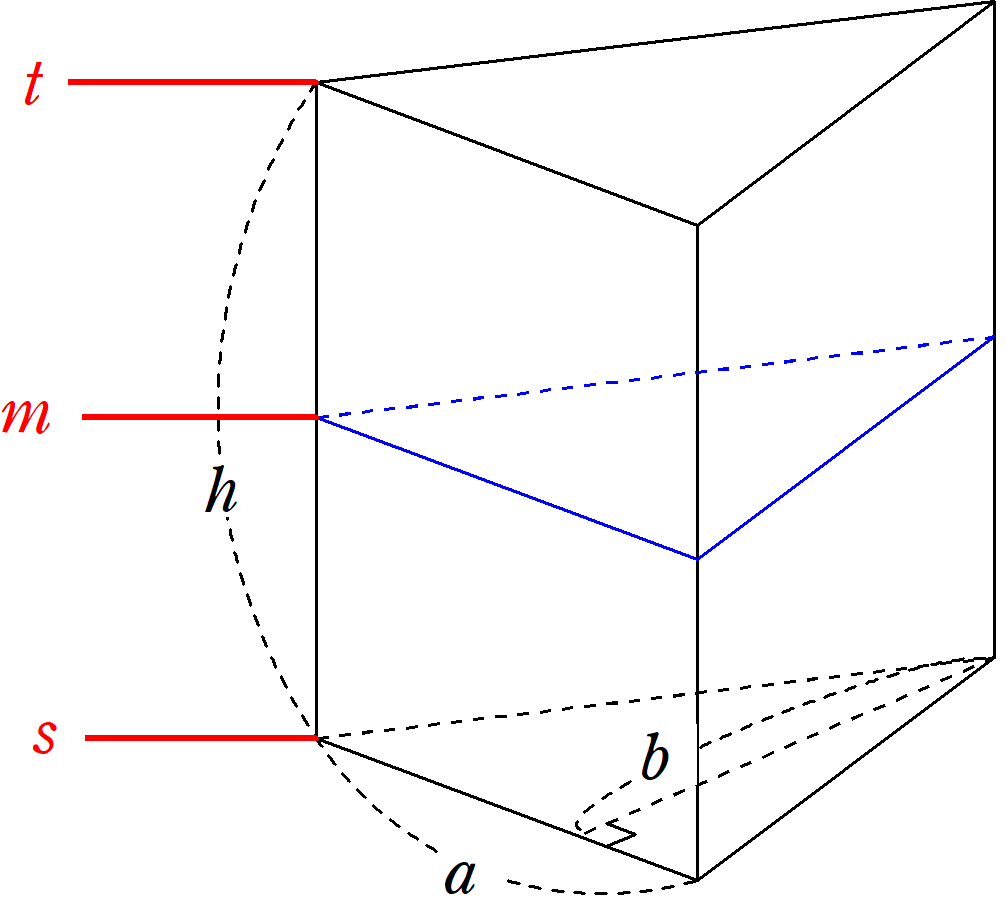
シンプソンの公式(応用編①)
シンプソンの公式は単純な積分のみならず、考え方次第では体積を求めるのにも使えます。 今回はその例をいくつか紹介します。 Ⅰ 体積への拡張 Ⅱ 三角柱の体積 Ⅲ 円錐... -

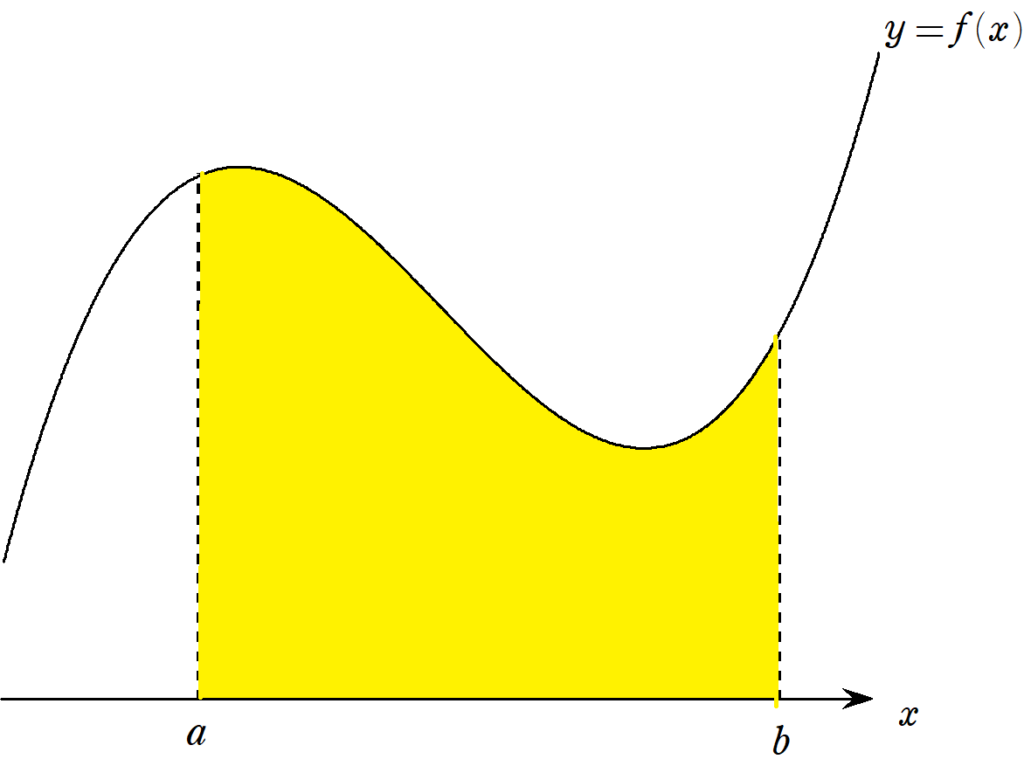
シンプソンの公式(基本編)
3次以下の関数の積分を求める際に使えるシンプソンの公式。まずは例と簡単な証明を与えます。 Ⅰ シンプソンの公式 Ⅱ 基本例 Ⅲ 反例 Ⅳ 証明1 【】 1743年、イギ...
1