数学ⅢC修了– tax –
-

メナイクモスが円錐曲線を導入!立方体倍積問題の解法を解説!【数学史6-19】
この記事では、古代ギリシャの数学者メナイクモスが立方体倍積問題を解くために円錐曲線を初めて使用したことを解説しています。メナイクモスは平面を異なる角度で切断することで、放物線、楕円、双曲線などを生み出し、これらを用いて立方体の体積を倍にする問題に取り組みました。 -

数学者のヒッピアスは円以外の曲線の発明者!円積線で三大作図問題が解ける!【数学史6-12】
三大作図問題の1つである「角の三等分問題」。この問題に初めて一定の成果を出したのは、古代ギリシャの数学者ヒッピアスでした。彼が発明した「円積線」を使うことで、角の三等分線は簡単に引くことができます。この記事では、ヒッピアスの人生について触れるとともに、円積線について細かく解説。円積線を式で表したり、なぜ円積線で角の三等分線が引けるのかを証明します。 -

永遠に到達できない?ゼノンの二分法のパラドックスを徹底解説!
ゼノンの二分法のパラドックスを解説し、その歴史的背景と現代数学における解決法を探ります。古代ギリシャ哲学者ゼノンによって提起されたこのパラドックスは、目的地に到達する前に無限の中間点を通過しなければならないという理由で、移動が不可能であると主張します。記事では、この直感に反する主張がどのように現代数学によって克服されているか、無限等比級数の概念を通じて説明しています。 -

アキレスと亀のパラドックスをわかりやすく解説!論破の鍵は収束する無限!
パラドックスの中で有名な「アキレスと亀」。足の速いアキレスが足の遅い亀に追いつくのは当然のように思えますが、古代ギリシャの哲学者ゼノンの考え方によれば追いつけなくなってしまいます。この記事では、ゼノンの考え方を図入りで説明しながら、パラドックスを解決する方法を紹介します。紀元前に無限の考え方を扱うのは難しかったようです。 -

「円周率の新しい求め方」ではない?話題の論文をざっくり解説!
2023年5月23日、高校生4人が円周率の新しい求め方を証明したという記事が、神戸新聞より掲載されました。しかし、その高校生たちが英語で書いた論文のタイトルは「円に内接する多角形の中で、面積が最大になるのは正多角形であることの初等的な証明」となっています。この記事では、その論文の内容をざっくりと解説!メディアの誇張に騙されないよう、論文の中身を大まかに理解しましょう。 -

三平方の定理の証明⑯~2023年最新!三角比を用いた証明をわかりやすく解説! 発見者は10代の少女?~
この記事では、数ある三平方の定理の証明の中でも、2023年最新の証明方法を紹介します。循環論法になりやすい三角比を使った珍しい証明方法です。話題になっている方法をどこよりもていねいに解説しています。 -

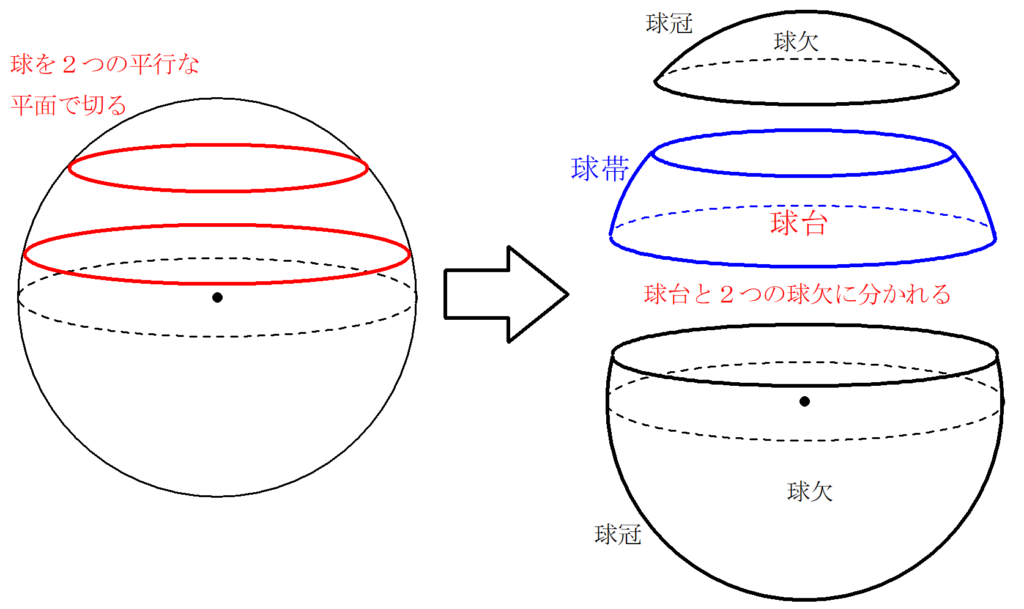
球台と球帯
球を2つの平面で切り取ってできた球台について考えます。 Ⅰ 球台と球帯とは? Ⅱ 球台の体積 Ⅲ 球帯の面積 【Ⅰ 球台と球帯とは?】 前記事の「球欠と球冠」同様... -

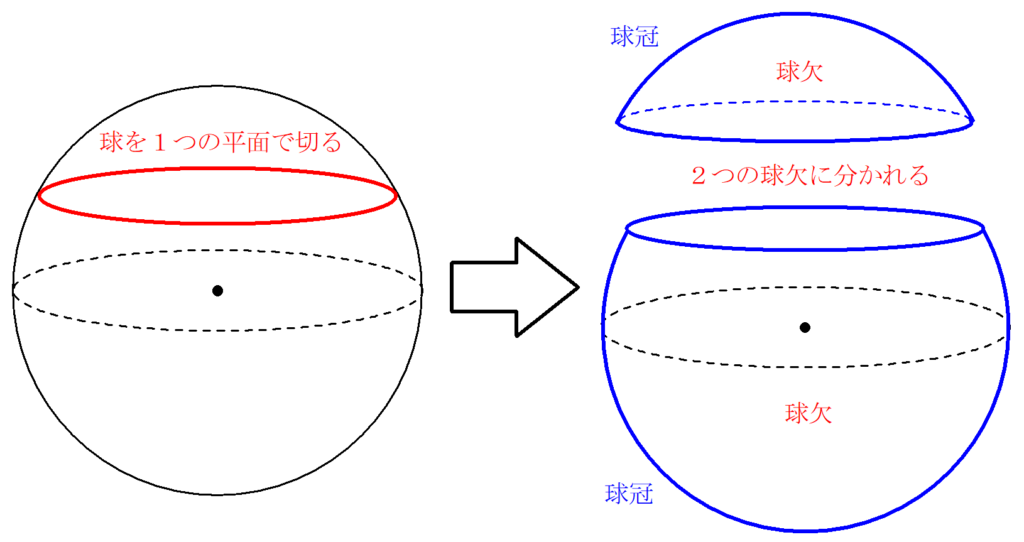
球欠と球冠
球を1つの平面で切り取ってできる球欠という立体について解説します。球欠の体積は、もとの球の半径に依存しない点が面白いです。 -

三平方の定理の証明⑩~無限等比数列による証明をわかりやすく解説! 無限を用いた珍しい証明方法とは?~
この記事では、数ある三平方の定理の証明の中でも、20世紀後半に登場した無限等比級数を利用した証明方法が解説します。その証明方法を考えた人物について触れると共に、どのように無限等比級数と直角三角形を繋げるのかを、多数の図を用いて解説しています。 -

平均値の定理の使い方をわかりやすく解説!証明はロルの定理を活用!
数学Ⅲで登場する平均値の定理。微分が絡み、登場する文字数が多いため、数式だけではなかなか理解しづらいのではないでしょうか。この記事では、平均値の定理の意味を例示でわかりやすく説明したうえで、ロルの定理を使って証明します。
12