2026ってどんな数？2026の素因数分解からハッピー数の性質を解説！

　数学好きや2026年の受験生必見！

　毎年新年を迎えるにあたり、西暦に関する数学ネタや西暦に関する受験問題について気になっている方も多いはず。

　そこで、西暦を使った数学ネタを毎年発信している数学史の先生Fukusukeが、$~2026~$という数が持っている性質を当たり前のものからマニアックなものまで解説！

• 2026年は約7年に1回のハッピー数の年
• $~2026~$は$~2~$と$~11~$で表せる
• $~\sqrt{2026}~$の連分数は$~45~$と$~90~$のみ

　2025年は$~45^2~$で美しい性質がたくさんありましたが、2026年は$~45^2+1~$であるということが、2026の美しい性質へと導いてくれます！

 この記事を書いた人 

Fukusuke（ふくすけ）
数学史の先生

1. 現役の中学・高校数学教員
2. 著書2冊重刷、ブログ累計200万PV達成
3. 行間がなくなるほど丁寧な式変形で執筆中
4. 「つむぎびより」「TSHファン」SEO監修

 この記事を書いた人 

Fukusuke（ふくすけ）
数学史の先生

• 現役の中学・高校数学教員
• 著書2冊は発売1ヶ月で即重刷
• 当数学史ブログは累計200万PV達成
• 行間がなくなるほど丁寧な式変形で記事を執筆
• 「つむぎびより」「TSHファン」のSEO監修を担当

『世界を変えた数学史図鑑』『教養としての数学史』好評発売中！

発売後即重刷の「読む数学ドラマ」
丸善日本橋店の2025年ベストセラー（理工書部門）に選ばれました！

Amazonで『教養としての数学史』を見る

楽天市場で『教養としての数学史』を見る

丸善日本橋店の2025年ベストセラー
（理工書部門）に選ばれました！

Amazonで
『教養としての数学史』を見る

楽天市場で
『教養としての数学史』を見る

2026を素因数分解してわかること

2026は2×1013の半素数

　まずは$~2026~$を素因数分解してみましょう。

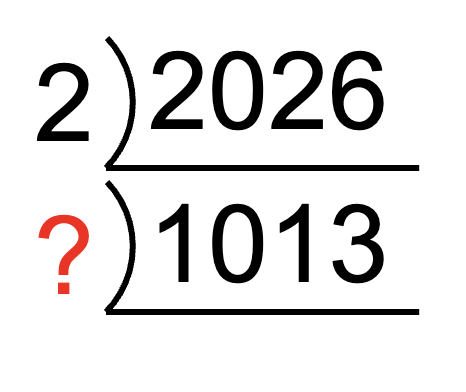
　偶数であることは自明ですが、$~1013~$は？
　実は、この$~1013~$は素数なので、素因数分解はこれで終わりです！

2026=2\times1013

　このように、2つの素数の積で表される自然数のことを半素数といいます。

　せっかくなので半素数の例をいくつか挙げてみましょう。

　このように、半素数自体はレアな数ではなく、$~2026~$は$~582~$番目の半素数なので、$~2026~$までの半素数の出現率は約28.7%。
　自然数の約4個に1個は半素数となります。

　ちなみに、素因数分解で出てくる$~1013~$という素数は、以下のような性質をもつことで割と有名な数です。

• 素数大富豪で2枚出しできる2番目に強い素数（10+Kで出せる。一番強いのはQ+K（1213））
• 標準大気圧が1013hPa
• $~1013^2=1026169~$をひっくり返すと$~3101^2=9616201~$

2026の約数は4個で総和は3042

　$~2026~$の素因数分解が$~2 \times 1013~$ と非常にシンプルなので、約数とその総和も簡単に求めることができます。

(1+1)\times (1+1)=4~(個)

\begin{align*}
&~~~~(1+2)(1+1013)   \\
&=3 \times 1014  \\
&=3042
\end{align*}

　素因数分解したときの素数の種類が2種類なので、次のような表にするとよりわかりやすいです。

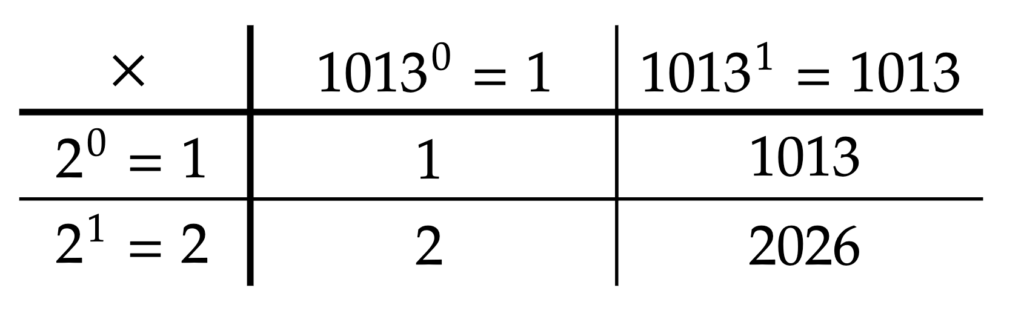
　また、自分自身（$~2026~$）を除いた約数の和は$~1 + 2 + 1013 = 1016~$ となり、これは$~2026~$より小さいため「不足数（自分自身を除いた和が自分自身よりも小さくなる自然数）」です。
　実は、半素数と不足数には次のような関係があります。

 半素数と不足数の関係の証明

(Ⅰ)　6以外の半素数が$~pq~$（$~p < q~$、$~p~$と$~q~$は素数）で表されるとき

　$~pq~$が不足数であるための条件は、約数の総和からその数自身を除いた数が、自分自身よりも小さくなければよいので、

\begin{align*}
(p+1)(q+1) - pq &< pq \\
pq + p + q + 1 - pq &< pq \\
1 &< pq - p - q \\
2 &< (p-1)(q-1) \cdots (*) 
\end{align*} 

である。

　(i) $~pq~$が偶数のとき（$~p = 2~$のとき）

　$~2q > 6~$より、$~q > 3~$で$~q~$は素数なので$~q \geqq 5~$。

　このとき、

\begin{align*} 
(p-1)(q-1) &\geqq (2-1) \cdot (5-1) \\
&= 4 \\
&> 2
\end{align*}

より、$~(*)~$を満たすため、$~pq~$は半素数である。

　(ii) $~pq~$が奇数のとき（$~p \geqq 3~$のとき）

　$~3 \leqq p < q~$より、$~q \geqq 5~$。

　このとき、

\begin{align*}
(p-1)(q-1) &\geqq (3-1)(5-1) \\
&= 8 \\
&> 2
\end{align*}

となり、$~(*)~$を満たすため、$~pq~$は半素数である。

　 (i), (ii)より、6以外の半素数$~pq~$は不足数であることが示された。

(Ⅱ)6以外の半素数が$~p^2~$（$~p~$は素数）で表されるとき

　$~p^2~$が不足数であるための条件は、(Ⅰ)と同様に考えて

\begin{align*}
(1+p+p^2) - p^2 &< p^2 \\
1+p &< p^2 \\
0 &< p^2-p-1
\end{align*}

である。

　ここで、$~f(p) = p^2-p-1~$とおくと、

f(p) = \left(p-\frac{1}{2}\right)^2 - \frac{5}{4}

で、$~f(2) = 2^2-2-1 = 1~$より、$~2 \leqq p~$において

f(p) = p^2-p-1 > 0

が成り立つ。

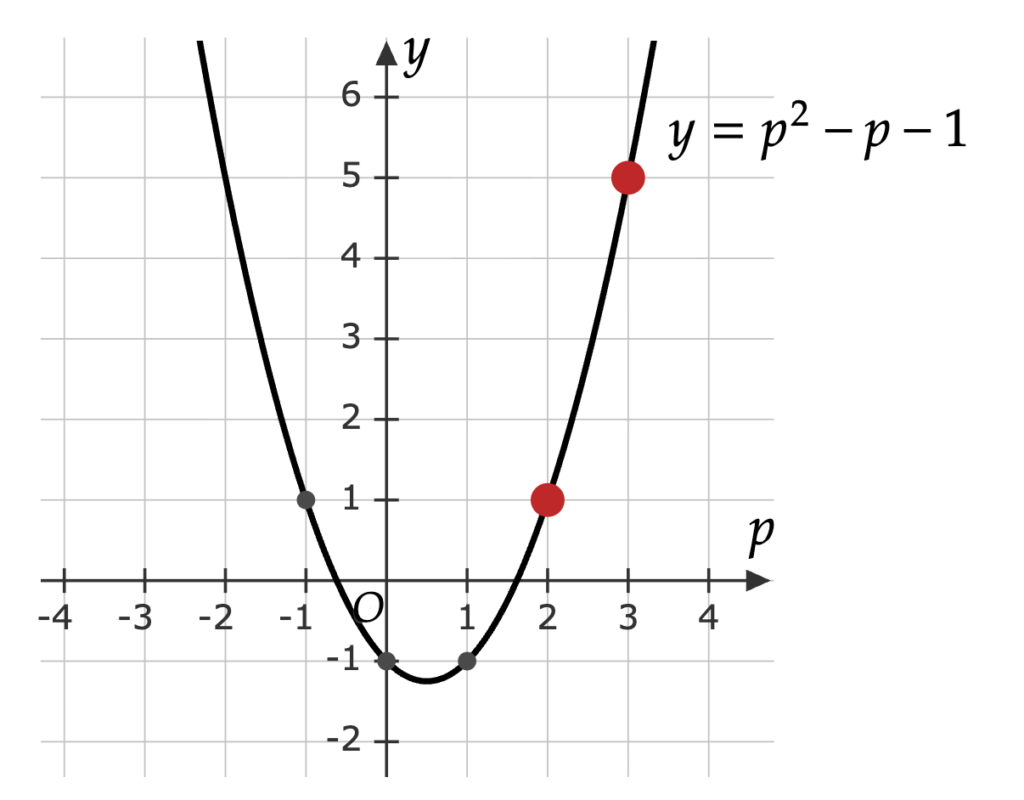
　よって、6以外の半素数$~p^2~$は不足数であることが示された。

　(Ⅰ), (Ⅱ)より、題意は示された。

　$~6~$の場合は$~p=2~,~q=3~$なので、$~(*)~$の右辺が

(2-1)(3-2)=2

となり、不等式が成り立ちません。
　実際、$~6~$は不足数ではなく完全数となります。

複素数による因数分解

　前年の2025年が$~45^2~$年であったことから、2026年は$~45^2+1~$年と表すことができます。

　これを利用することで、複素数の範囲において、以下のように因数分解ができます。

2026 = (45+i)(45-i)

　これは$~2026~$という数が、2つの平方数の和で表されることによるもの。
　平方数の和で表されるという事実は、他にも美しい性質を$~2026~$に与えてくれます。（後述）

2026はハッピー数

　$~2026~$の性質の中で、最も特徴的なのは「ハッピー数」です。

ハッピー数の定義と例

　あまり聞きなれないかもしれませんが、ハッピー数は以下の定義で与えられます。

　実際に$~7~$と$~8~$を例に、ハッピー数かどうかの計算をしてみましょう。

　ハッピー数は、自然数全体の中で約7分の1の割合で存在する、比較的レアな数です。

　ちなみに、ハッピー数ではない場合、$①$と$②$の間で見たような$~4~$を含む無限ループに入ってしまいます。
　このような、ハッピー数ではない数のことをアンハッピー数といいます。

302番目のハッピー数が2026

　それでは、2026がハッピー数であることを確認してみましょう。

　見事に$~1~$にたどり着きました！

　$~2026~$は302番目のハッピー数であり、$~2026~$までのハッピー数の個数の割合は約$~14.9%~$。
　確かに約$~\displaystyle \frac{1}{7}~$がハッピー数です。

　ちなみに、$~2000~$以上$~2100~$以下のハッピー数は以下の13個。

2001,2003,2008,2019,2026,2030,2036,2039,2062,2063,2080,2091,2093

　$~2039~$と$~2062~$の間は幸さちが薄いですね。

2026は平方和で表せる

　　$~2026~$は2つの自然数の平方和として表すことができます。

2026=45^2+1^2

　このことが、以下に挙げるような美しい関係性を生み出しています。

1013の平方和との美しい関係

　$~2026~$を素因数分解したときに出てくる$~1013~$。
　実はこの$~1013~$も2つの自然数の平方和で表せます。

1013 = 22^2 + 23^2

　この式から、次のような美しい式が導けます。

\frac{45^2+1^2}{2}=\left(\frac{45-1}{2}\right)^2 + \left(\frac{45+1}{2}\right)^2 

√2026は45と90で連分数展開ができる

　$~2026=45^2+1^2~$であることから、その正の平方根である$~\sqrt{2026}~$の連分数展開は非常に美しい形になります。

　連分数とは、分母にさらに分数が含まれるような、入れ子構造の分数のことです。
　実際に式変形を見てみましょう。

\begin{align*}
\sqrt{2026} &= 45 + (\sqrt{2026} - 45) ~~~\cdots ① \\
\\
&= 45 + \frac{(\sqrt{2026} - 45)(\sqrt{2026} + 45)}{\sqrt{2026} + 45} \\
\\
&= 45 + \frac{2026 - 2025}{45 + \sqrt{2026}} \\
\\
&= 45 + \frac{1}{45 + \sqrt{2026}} \\
\\
&= 45 + \frac{1}{45 + 45 + \sqrt{2026} - 45} \\
\\
&= 45 + \frac{1}{90 + (\sqrt{2026} - 45)} ~~~\cdots ② \\
\\
&= 45 + \frac{1}{90 + \frac{(\sqrt{2026} - 45)(\sqrt{2026} + 45)}{\sqrt{2026} + 45}} \\
\\
&= 45 + \frac{1}{90 + \frac{1}{45 + \sqrt{2026}}} \\
\\
&= 45 + \frac{1}{90 + \frac{1}{45 + 45 + \sqrt{2026} - 45}} \\
\\
&= 45 + \frac{1}{90 + \frac{1}{90 + (\sqrt{2026} - 45)}} ~~~\cdots ③  \\
\\
&~~~~~~~~~~~~~~~~~~~~~~~~~~~\vdots
\end{align*}

　上記の式変形を見ると、$~①~$と$~②~$と$~③~$で$~(\sqrt{2026}-45)~$という多項式が登場しているのがわかります。
　以降も同様の式変形が可能なので、5回ほど続けると、以下のような式が出てきます。

\sqrt{2026} = 45 + \cfrac{1}{90 + \cfrac{1}{90 + \cfrac{1}{90 + \cfrac{1}{90 + \cfrac{1}{90 + (\sqrt{2026} - 45)}}}}}

　そして、連分数展開を利用することで、以下のように$~\sqrt{2026}~$の近似値が得られます。

\sqrt{2026} \fallingdotseq45 + \cfrac{1}{90}=45.0111111111\cdots

\sqrt{2026} \fallingdotseq45 + \cfrac{1}{90 + \cfrac{1}{90}}=45.0111097395\ldots

　実際の値は$~\sqrt{2026} \fallingdotseq 45.0111097397~$なので、2回目の段階でかなりの精度を持っていることがわかります。

　連分数展開がこれほど美しい結果になるのは$~2026~$が$~n^2+1^2~$の形をしているからです。

\begin{align*}
 &~~~~\sqrt{n^2+1^2} \\
&= n + (\sqrt{n^2+1} - n) \\
&= n + \frac{(\sqrt{n^2+1} - n)(\sqrt{n^2+1} + n)}{\sqrt{n^2+1} + n} \\
&= n + \frac{n^2+1-n^2}{\sqrt{n^2+1} + n} \\
&= n + \frac{1}{\sqrt{n^2+1} + n}
\end{align*}

　連分数展開では分子を$~1~$に揃えることが多いため、同じ平方数の和でも$~\sqrt{2029}=\sqrt{45^2+2^2}~$では、今回の$~\sqrt{2026}~$のようにうまくいきません。

2026に関する性質や数式

　最後に、2026に関するおもしろい数式や性質を3つ紹介します。

2の累乗による美しい数式

　$~2026~$は$~2~$と$~11~$という$~2~$種類の数によって、以下のように表せます。

2026 = 2^{11} - 2 \times 11

　$~2~$と$~11~$が美しく配置された数式ですね。

　また、この数式を少しいじると、$~2~$だけを使って$~2026~$を表せます。

2026 = \sqrt{2^{22}} - 22

2026を法とすると45は虚数？

　もう一つ、合同式を使った面白い性質を見てみましょう。

　$~2026 = 45^2 + 1~$から、次の合同式が言えます。

45^2 = 2025 \equiv -1 \pmod{2026} 

　これは、$~45^2~$を$~2026~$で割った余りが$~-1~$（すなわち$2025$）になるという意味です。

　この式の両辺をさらに2乗すると、次のような整った合同式が誕生します。

45^4 \equiv 1 \pmod{2026}

　こちらは、$~45^4~$を$~2026~$で割った余りが$~1~$ということです。

　$~2026~$を法としたときに出てくる$~45^2 \equiv -1~$という数式は、合同式の世界において、$~45~$がまるで虚数単位$~i~$のように振る舞うことを示唆しています。

　そのため、$~45~$の累乗はを$~2026~$で割ったときの余りは、次のような周期4の繰り返しになるのです。

　少し無理やりな着眼点でしたが、$~2026~$を法としたときの$~45~$が$~i~$と同じ構造になるのが面白いですね。

90,2024,2026で直角三角形が作れる

　$~2026~$を斜辺にもつ、三辺の長さが整数値の直角三角形を考えてみると、$~90~,~2024~,~2026~$の1通りしかありません。

　この直角三角形を図にしてみると、下のような細長いものになります。

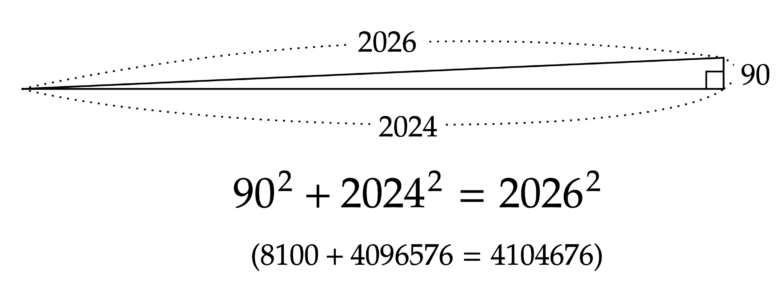
　ちなみに、とがっている部分の角度は約$~2.5^{\circ}~$です。

\sin^{-1}{\frac{90}{2026}}\fallingdotseq2.5^{\circ}

まとめ

　今回は、2026という数が持つ様々な数学的性質を探求しました。

• $~2 \times 1013~$という半素数（1013は素数）
• 各位の2乗和を繰り返すと$~1~$になる（302番目のハッピー数）
• $~2026=45^2+1^2~$と$~1013=22^2+23^2~$の美しい関係
• $~ \sqrt{2026}~$の連分数展開は90が連なる美しい形
• $~2^{11}-2×11~$という美しい式
• $~2026~$を法としたときの45が、虚数単位$~i~$と同じ構造

　2026年は2025年の次の年ということで、それに由来する性質が目白押しでした。

　2026年、ハッピーな年になりますように。

あわせて読みたい

2025はどんな数？素因数分解や約数、九九表に関わる美しい性質を解説！ 2025年が持つ数学的な特徴や性質を詳述。平方数、九九表の和、素因数分解の応用などを通じて、西暦の数字の新たな一面を紹介します。数学ファンや受験生必見の内容です！