タレスの定理～中学3年生で習う円の定理を解説！証明は超簡単！～

2022年11月6日2025年7月16日

当ページのリンクには広告が含まれています。

　古代ギリシャの数学者で、「数学の祖」とも呼ばれるタレス。

　彼の名を冠する「タレスの定理」は5つの命題を指すものの、最も有名なのは「半円に内接する三角形は直角三角形となる」というもの。

　中学3年生の円周角の定理で出てくるレベルの内容で、証明も非常に簡単なものとなっています。

　この記事では、最も有名なタレスの定理の命題を証明すると共に、他の4つの命題についても解説します。

この記事を書いた人

Fukusuke（ふくすけ）
数学史の先生

現役の中学・高校数学教員
著書2冊重刷、ブログ累計200万PV達成
行間がなくなるほど丁寧な式変形で執筆中

この記事を書いた人

Fukusuke（ふくすけ）
数学史の先生

現役の中学・高校数学教員
著書2冊は発売1ヶ月で即重刷
当数学史ブログは累計200万PV達成
行間がなくなるほど丁寧な式変形で記事を執筆

『世界を変えた数学史図鑑』『教養としての数学史』好評発売中！

この記事を読んでわかること

タレスの定理とは？

　タレス（Thales , B.C.625頃～B.C.547頃）は古代ギリシャの数学者です。

　彼は数学の定理を初めて証明したことから、「数学の祖」や「最初の数学者」などと呼ばれています。

Fukusukeの数学めも

404: ページが見つかりませんでした | Fukusukeの数学めも

世界で最初に証明された定理

　タレスが初めて証明した定理こそ、現在「タレスの定理」と呼ばれている定理です。

　内容としては、中学3年生の「円」の単元で習う円周角についてのもの。

タレスの定理 (1)

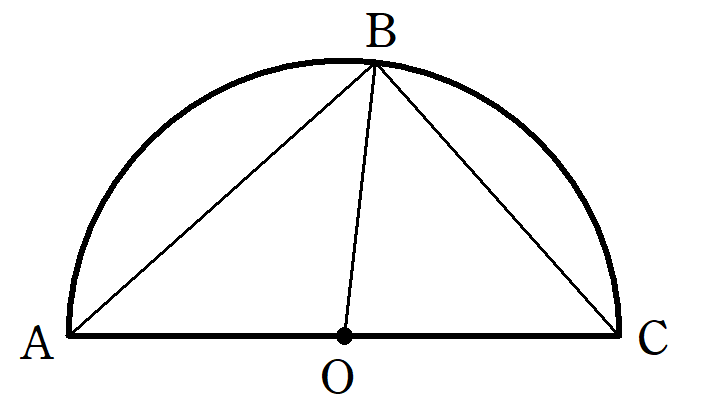
　半円に内接する三角形は直角三角形である。

　解釈の仕方によっては、

半円に内接する角は直角である。
$~\triangle ABC~$の3つの頂点$~A~,~B~,~C~$が円周上の異なる点にあり、辺$~AC~$が直径となるとき、$~\angle ABC=90^{\circ}~$である。

などとも表現されます。

　この定理は、タレスがバビロニアに旅行した際に知り、自身の出身地であるミレトスに帰ってきた後に証明を行いました。

証明は二等辺三角形を使うだけ

　タレスの定理の一般的な証明を下に示します。

タレスの定理(1)の証明

　図3において、円$~O~$の半径より、

OA=OB=OC

なので、$~\triangle OAB~,~\triangle OCB~$は二等辺三角形となる。

　二等辺三角形の底角は等しいので、

\begin{align*} \angle OAB &=\angle OBA=x \\ \angle OCB &=\angle OBC=y \\ \end{align*}

とおける。

　このとき、$~\triangle ABC~$の内角の和より、

\begin{align*} x+x+y+y&=180^{\circ} \\ 2x+2y&=180^{\circ} \\ x+y&=90^{\circ} \end{align*}

　したがって、$~\angle ABC=x+y=90^{\circ}~$が示された。$~~\blacksquare~$

　三角形の内角の和が$~180^{\circ}~$であることは、ピタゴラス学派が最初に発見・証明したと言われているため、タレスは上記のような証明はできなかったと推測されています。

　タレスが実際に行った証明方法は、長方形に外接する円を描くような視覚的で素朴な方法ではないかと推測されています。

　しかし、何かしらの証明方法を発見したことは確かで、１頭の牡牛を神に捧げるほどタレスは狂喜しました。

広義のタレスの定理

　「タレスの定理」と言えば、先ほどのタレスの定理(1) を指すことが多いです。

　しかし、それ以外にも4つの定理が「タレスの定理」と称されることがあります。

タレスが証明をしなかった4つの「タレスの定理」

　タレスの功績として扱われるのは、タレスの定理(1) の他、以下の4つの定理です。

タレスの定理 (2)

　円の直径は円を二等分する。

　タレスが論証したと言われているものの、直径を何本か書くことで図示しただけのようです。

タレスの定理 (3)

　二等辺三角形の底角は等しい。

　中学2年生で習い、証明まで行う二等辺三角形の性質ですが、タレスは定理の内容を陳述しただけのようです。

タレスの定理 (4)

　2本の直線が交わってできた対頂角は等しい。

　こちらも中学2年生で習い、証明まで行う図形の性質。
　タレスが発見したものの、証明はしませんでした。

タレスの定理 (5)

　2つの三角形の2つの角と1つの辺とがそれぞれ等しければ、それらの三角形は合同である。

　中学2年生で習う合同条件の1つ。
　証明こそしなかったものの、海上の船までの距離を測量するときの考え方に応用しました。

ユークリッドの『原論』では証明された

　タレスが生きていた時代から約300年後。

　タレスの定理は、ユークリッド（Euclid, B.C.330頃-B.C.275頃）の主著『原論』にも採用されました。

　タレスの定理(1)～(5)はそれぞれ、『原論』の以下の命題に対応しています。

（※『原論』の命題の文章は https://pisan-dub.jp/doc/2011/20110205001/index.html より引用）

(1)　半円に内接する三角形は直角三角形である。
→　円において、半円内の角は直角であり、半円より大きい切片内の角は直角より小さく、半円より小さい切片内の角は直角より大きい。また、半円より大きい切片の底角は直角より大きく、半円より小さい切片の底角は直角より小さい。（『原論』命題Ⅲ－31）

(2)　円の直径は円を二等分する。
→　直径とは、円の中心を通り、円周上に両端をもつ直線であり、それによって円は二分される。（『原論』定義Ⅰ－17）

(3)　二等辺三角形の底角は等しい。
→　二等辺三角形の底辺上の二つの角は互いに等しい、そして、等辺を延長してできる底辺下の二つの角も互いに等しい。（『原論』命題Ⅰ－5）

(4)　2本の直線が交わってできた対頂角は等しい。
→　二つの直線が交わるとき、その対頂角は互いに等しい。（『原論』命題Ⅰ－15）

(5)　2つの三角形の2つの角と1つの辺とがそれぞれ等しければ、それらの三角形は合同である。
→　二つの三角形において、二角がそれぞれ等しく、ある一辺が等しければ、残りの二辺もそれぞれ等しく、残りの角も等しい。（『原論』命題Ⅰ－26）

　タレスの定理(1)～(5) の中には、『原論』では「定義」とされたものもあり、タレスが証明に苦慮していたことがわかります。

　しかし、タレスがタレスの定理(1) を証明したことは、ピタゴラスやユークリッドをはじめとする後世の数学者たちに影響を与えており、現在の数学もその流れを受け継いでいるのです。

まとめ

　世界で最初に証明された定理である、「タレスの定理」について解説してきました。

「タレスの定理」と呼ばれる定理は5種類ある。
タレスが実際に証明できたのは1種類だったが、論証数学の先駆けとなった。
残りの4種類の定理については、ユークリッドの『原論』で言及、定義とされた。

　古代ギリシャの数学者タレスの年譜や面白エピソードも、是非のぞいてみてください↓

Fukusukeの数学めも

404: ページが見つかりませんでした | Fukusukeの数学めも

バビロニアとかで当たり前のように知られていた定理について、なぜ成り立つかを証明してみようと考えるなんて、タレスは疑い深い人だったんだね。

　当時のギリシャ人は法で統治されたポリスの中で、市民どうしの議論が活発だったから、相手に反論の隙を与えない説明が必要だったんだ。
　それゆえに、数学においても証明が必要とされたんだよ。

◇参考文献等
・三浦伸夫・三宅克哉監訳,久村典子訳（2018）『メルツバッハ＆ボイヤー　数学の歴史Ⅰー数学の萌芽から17世紀前期までー』,pp.43-45,朝倉書店.
・ジョニー・ボール著,水谷淳訳（2018）『数学の歴史物語』,pp.20-24,SB Creative.
・Bertrand Hauchecorne,Daniel Suratteau（2015）『世界数学者事典』,pp.273-275,熊原啓作訳,日本評論社.
・ポール・パーソンズ、ゲイル・ディクソン（2021）『図解教養事典　数学』,p.17,NEWTON PRESS
・志賀浩二（2014）『数学の流れ30講（上）ー16世紀までー』,pp.27-28,朝倉書店.
・マイケル・Ｊ・ブラッドリー（2009）『数学を切りひらいた人びと１－数学を生んだ父母たち』,pp.16-20,松浦俊輔訳,青土社.
・ピエルジョルジョ・オーディフレッディ著,河合成雄訳（2021）『幾何学の偉大なものがたり』,pp55-68,創元社.

タレスの定理～中学3年生で習う円の定理を解説！証明は超簡単！～