\pi=3.1415926535\cdots
円周率$~π~$は、古代から現代まで数多くの数学者を魅了してきた不思議な定数です。
円周率の値を求めるために、紀元前から多くの数学者たちが試行錯誤を重ね、現在では100兆桁以上わかっています。
円周率を精密に求める方法は、時代と共に進化してきました。
紀元前では正多角形で円を近似するという方法が使われていたものの、微分積分学の発展に伴い現在は級数によって直接円周率が求められています。
この記事では特に、ヘレニズム時代の天才数学者アルキメデスが利用した正多角形による計算法を紹介!
現役数学教員で数学史ライターのFukusukeがたくさんの図とともにわかりやすく解説します。
コンピュータのない時代、アルキメデスたちがいかにして円周率の値を求めようとしたのか、思考の跡を一緒にたどりましょう。
円周率の求め方は大きく2通り
数学史上、円周率は大きく分けて2通りの方法で求められてきました。
求め方1:正多角形ではさむ
これは紀元前3世紀の数学者アルキメデスが考案した古典的な方法で、古代中国では「割円術」と呼ばれました。
円に内接・外接する正多角形の周の長さを計算し、円周の長さを両側からはさむことで円周率を近似します。
例として、正六角形で円を内接・外接させた場合、以下のような関係がわかります。

下の図からわかるように、正多角形の辺の数を増やせば増やすほど、円に近づきます。

アルキメデスに始まり、以下のような数学者たちがこの方法で円周率の値を細かく求めました。
| 年 | 数学者 | 国 | 求めた円周率の桁数 | 正多角形の辺の数 |
|---|---|---|---|---|
| 紀元前3世紀 | アルキメデス | ギリシア | 小数第2位まで | 96 |
| 3世紀 | 劉徽(りゅうき) | 中国 | 小数第3位まで | 192 |
| 480年頃 | 祖沖之(そちゅうし) | 中国 | 小数第7位まで | 24,576 |
| 1610年 | ルドルフ・ファン・ケーレン | オランダ | 小数第35位まで | $~2^{62}~$(約461京) |
求め方2:無限級数を計算する
解析学が発展した17世紀以降は、無限級数を用いた計算法が主流になりました。
その計算式や証明方法については、改めて別の記事で紹介しますが、初期の例として有名なものを2つ挙げます。
\frac{\pi}{6}=\sum_{n=0}^{\infty}\left\{\frac{(-1)^n}{2n+1}\cdot \left(\frac{1}{\sqrt{3}}\right)^{2n+1} \right\} \frac{\pi}{4}=\sum_{n=0}^{\infty}\left\{ 4 \cdot \frac{(-1)^{n}}{2n+1} \cdot \left( \frac{1}{5} \right)^{2n+1}+\frac{(-1)^{n+1}}{2n+1} \cdot \left( \frac{1}{239} \right)^{2n+1} \right\}イングランドの数学者エイブラハム・シャープ (Abraham Sharp , 1653〜1742)は、1699年にシャープの公式により、小数点以下71桁まで求めました。

(出典:William Cudworth, Public domain, via Wikimedia Commons)
同じくイングランドの数学者ジョン・マチン(John Machin , 1680〜 1751)は、17110年にマチンの公式により、小数点以下100桁まで求めました。

(出典:See page for author, Public domain, via Wikimedia Commons)
その後も円周率に近づくのが速い級数が開発され、20世紀にはコンピュータが誕生したことによって円周率の計算が飛躍的に向上。
2025年4月2日現在、円周率は300兆桁まで計算されています。
正多角形ではさむ求め方
解析学が登場するまで、円周率を求める方法として使われた正多角形による近似。
ルドルフ・ファン・ケーレンは正$~2^{62}~$角形を利用していますが、どのように辺の長さを求めたのでしょうか。
数列の関係式から数値計算を行う
実は、正多角形の辺の数を$~3~,~4~,~5~,~6~,\cdots~$と増やしていったわけではありません。
アルキメデスであれば、正6角形から始めて、$~6~,~12~,~24~,~48~,~96~$と辺の数を2倍ずつ増やしてきました。
なぜなら、以下のような関係式が求められたからです。
直径 $1$ の円に内接する正 $n$ 角形の周の長さを $a_n$ 、外接する正 $n$ 角形の周の長さを $b_n$ とする。
このとき、次の2つの式が成り立つ。
\begin{cases}
a_{2n} = \sqrt{a_n b_{2n}} \quad \\
\\
\displaystyle b_{2n} = \frac{2 a_n b_n}{a_n + b_n}
\end{cases}円に内接する正六角形の周の長さ$~a_6~$と、外接する正六角形の周の長さ$~b_6~$から始めた場合、次のような順番で$~\{a_n\}~$と$~\{b_n\}~$が交互に求められます。
a_6,b_6\xrightarrow{下の式}b_{12}\xrightarrow{上の式}a_{12}\xrightarrow{下の式}b_{24}\xrightarrow{上の式}a_{24}\xrightarrow{下の式}\cdots直径$~1~$の円の円周の長さは$~\pi~$であり、その値は内接する多角形の周の長さ$~a_n~$より大きく、外接する多角形の周の長さ$~b_n~$より小さいので、$~\{a_n\}~$と$~\{b_n\}~$が求められていくにつれ、$~\pi~$の真値に近づきます。

関係式の証明方法
内接多角形の周$~\{a_n\}~$と、外接多角形の周$~\{b_n\}~$を求めるための公式を証明してみましょう。
証明に使う知識は三角比ですが、アルキメデスや劉徽、祖沖之の時代には三角比が無かったため、相似を繰り返し使って同様の公式を求めました。
まずは、証明のための補題を2つ挙げます。
半径 $r$ の円 $O$ について, 弦 $AB$ の長さは, $\angle AOB = \alpha$ とすると、次の式で与えられる。
AB = 2r \sin \frac{\alpha}{2}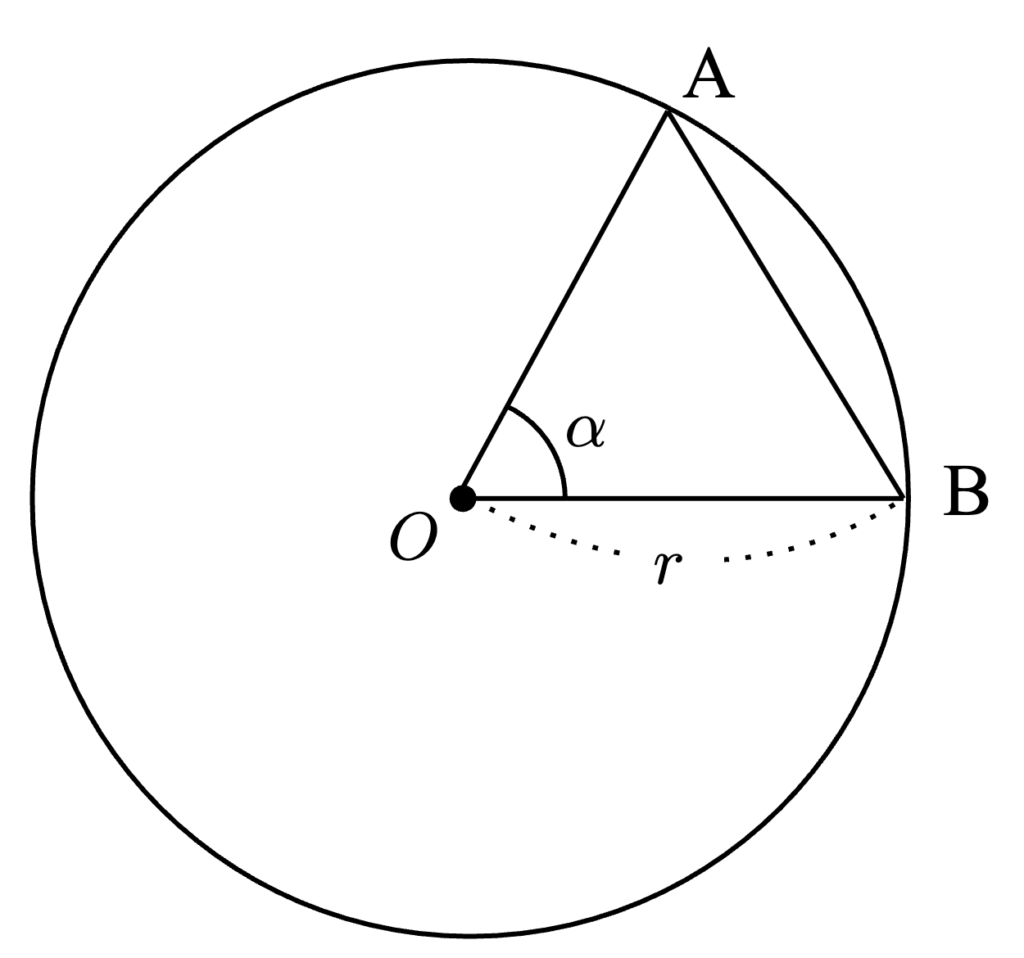
半径 $r$ の円 $O$ について、$O$ 上の点 $T$ における接線をひく。
接線上に $AT = BT$ となる異なる $2$ 点 $A, B$ をとり、$\angle AOB = \alpha$ とするとき、線分 $AB$ の長さは次の式で与えられる。
AB = 2r \tan \frac{\alpha}{2} 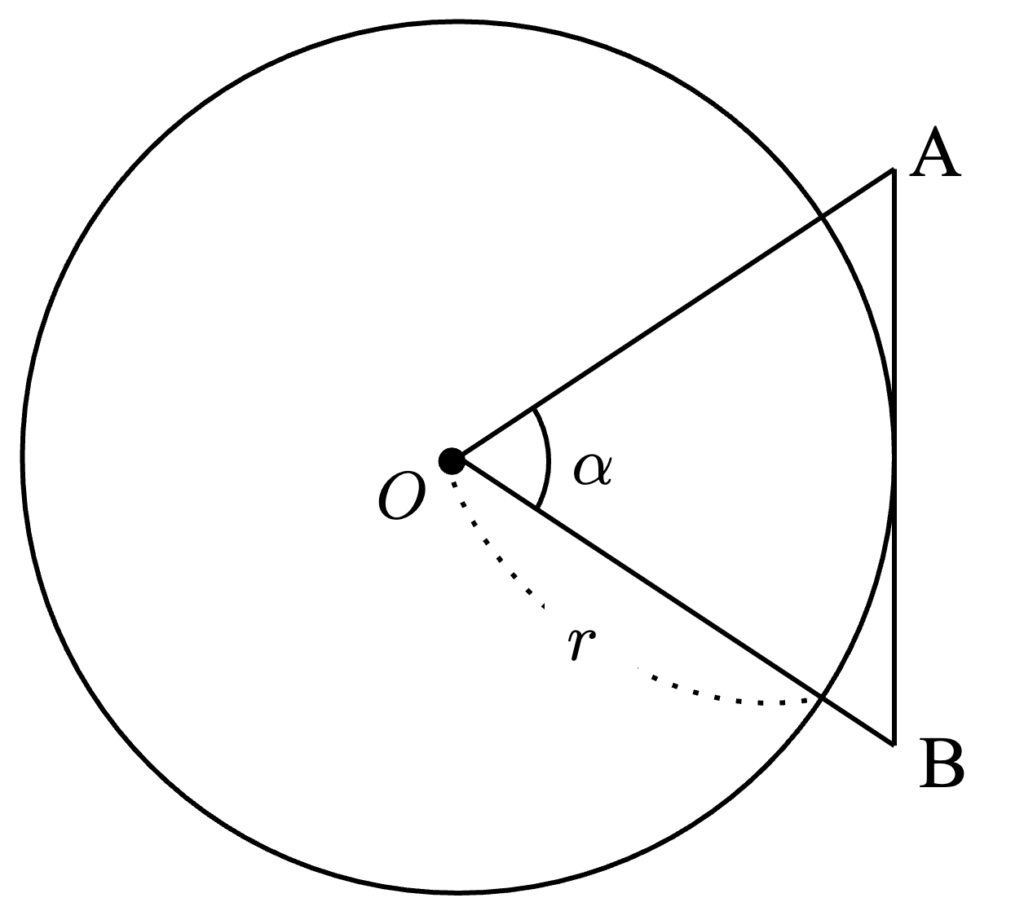
これらの補題は、三角比の定義から簡単に証明されます。
中心 $O$ から $AB$ への垂線の足を $H$ とする。

このとき、$~\displaystyle \angle HOA = \frac{\alpha}{2}$ なので、$\triangle HOA$ で三角比の定義から
HA = r \sin \frac{\alpha}{2}とわかる。
$\triangle OAB$ は二等辺三角形なので、
AB = 2HA = 2r \sin \frac{\alpha}{2}が求められた。$~\blacksquare~$
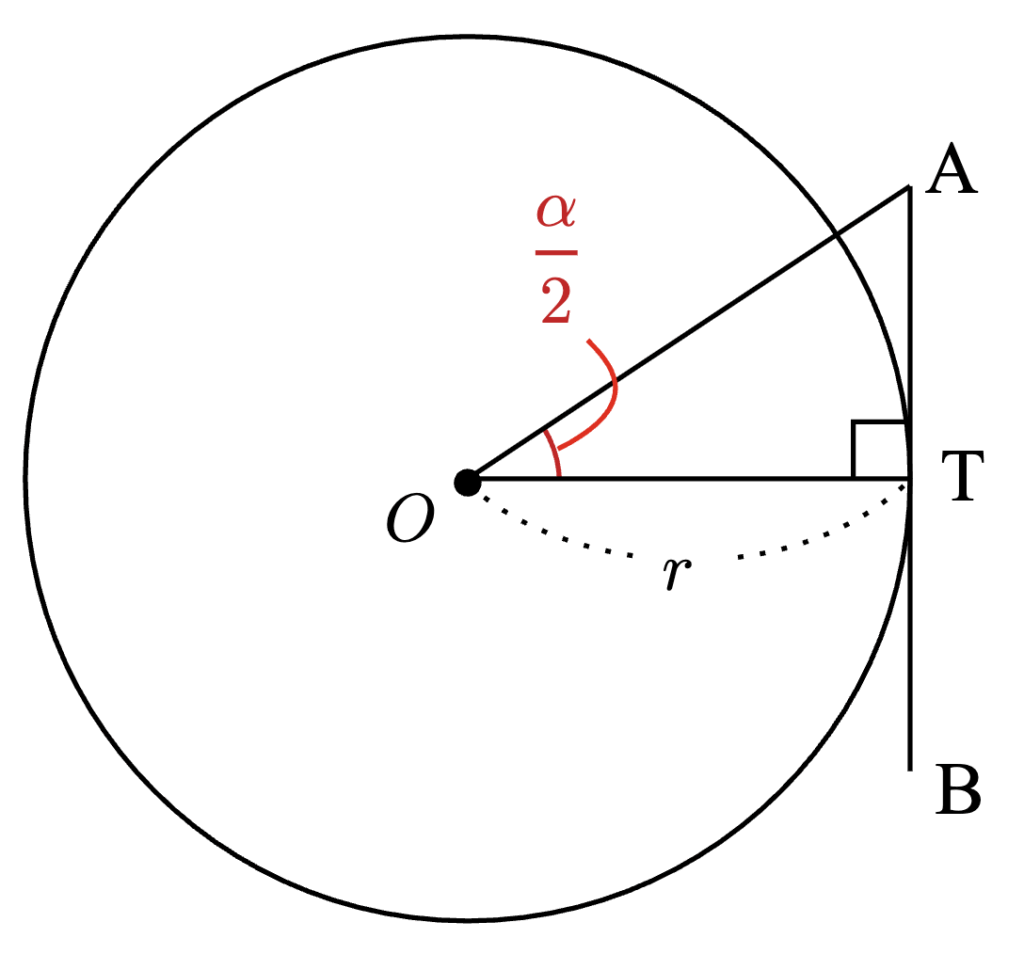
$\triangle OAT$ で、$\angle AOT = \frac{\alpha}{2}$ なので三角比の定義から
AT = r \tan \frac{\alpha}{2}とわかる。
したがって、$AT = BT$ より、
AB = 2AT = 2r \tan \frac{\alpha}{2}が求められた。$~\blacksquare~$
補題1と補題2が証明されたところで、本題である2つの関係式の証明に入りましょう。
まず、内接する正 $n$ 角形について考える。
各頂点と中心を結んだとき、周の長さは $a_n$ なので、各弦の長さは $\displaystyle \frac{a_n}{n}$, 中心角は $\displaystyle \frac{360^{\circ}}{n}$, 半径は $\displaystyle \frac{1}{2}$ となる。

補題1 より、
\begin{align*}
\frac{a_n}{n} &= 2 \cdot \frac{1}{2} \cdot \sin \frac{180^{\circ}}{n} \\
\\
a_n &= n \sin \frac{180^{\circ}}{n}
\end{align*}であり、ここで、$\displaystyle \frac{180^{\circ}}{n} = 2\theta$ とおくと、
a_n = n \sin 2\theta \quad \cdots ①
と求められる。
同様に内接する正 $2n$ 角形を考える。
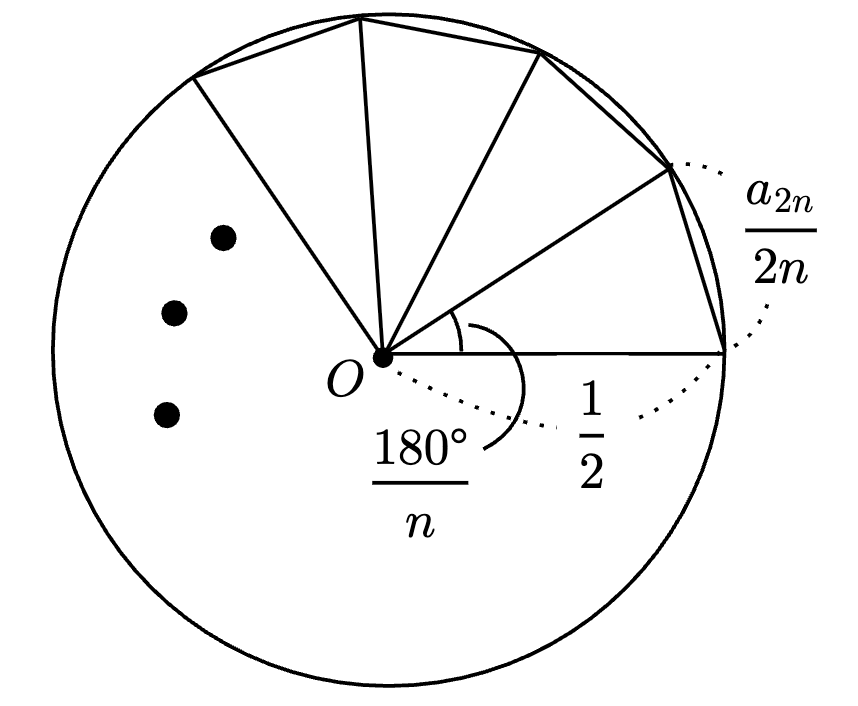
\begin{align*} \frac{a_{2n}}{2n} &= 2 \cdot \frac{1}{2} \cdot \sin \frac{90^{\circ}}{n} \\
\\
a_{2n} &= 2n \sin \frac{90^{\circ}}{n} \\
\\
a_{2n}& = 2n \sin \theta \quad \cdots ② \end{align*}と求められる。
次に、外接する正$n$角形について考える。
各頂点と中心を結んだとき、周の長さは$~b_n~$なので、各接線を切り取った線分の長さは$~\displaystyle \frac{b_n}{n}$、中心角は$~\displaystyle \frac{360^{\circ}}{n}~$となる。
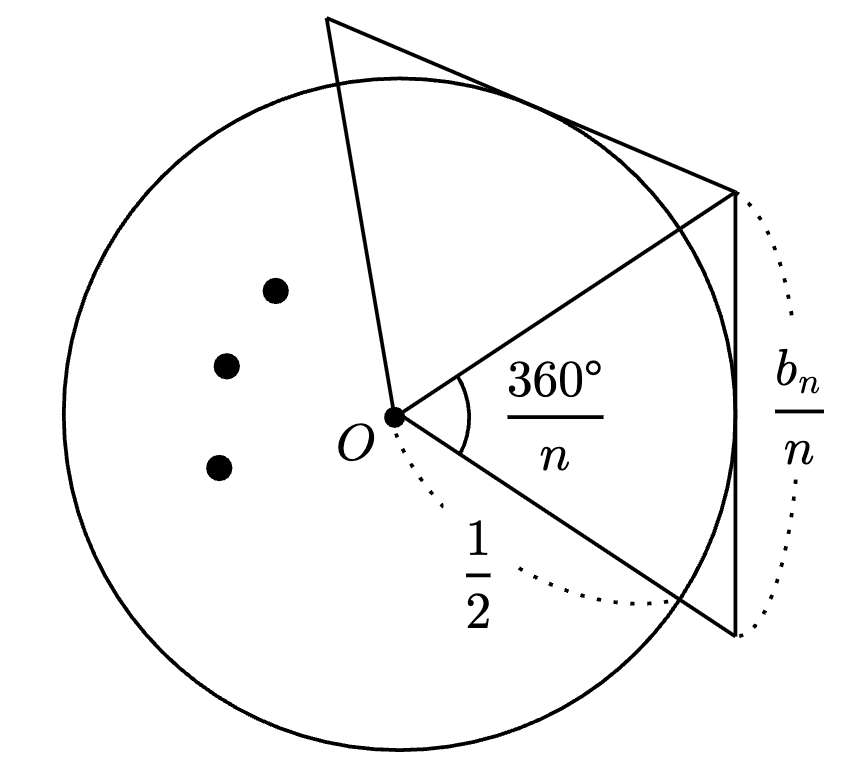
半径は$~\displaystyle \frac{1}{2}~$なので、補題2より、
\begin{align*} \frac{b_n}{n} &= 2 \cdot \frac{1}{2} \cdot \tan\frac{180°}{n} \\
\\
b_n &= n \tan\frac{180°}{n} \\
\\
b_n &= n \tan 2\theta \cdots ③
\end{align*} と求められる。
同様に、 円周に外接する正$~2n~$角形を考える。
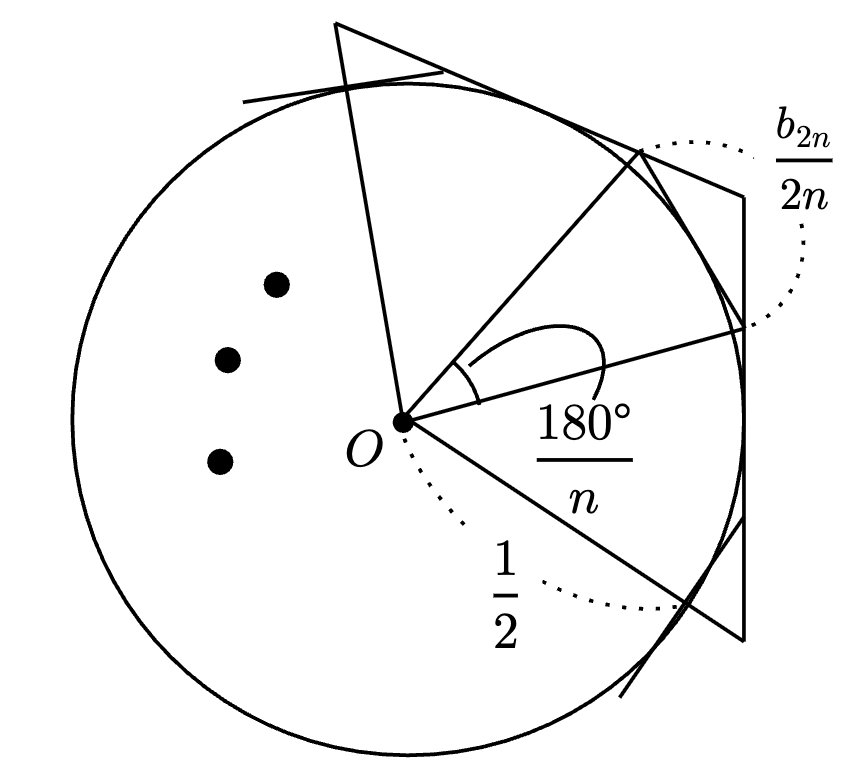
\begin{align*} \frac{b_{2n}}{2n} &= 2 \cdot \frac{1}{2} \cdot \tan\frac{90°}{n} \\
\\
b_{2n} &= 2n \tan\frac{90°}{n} \\
\\
b_{2n} &= 2n \tan \theta \cdots ④
\end{align*} と求められる。
$①$〜$④$を利用して、$~\displaystyle b_n = \frac{2a_n b_n}{a_n + b_n}~$を示す。
右辺に$①$、$③$を代入すると、
\begin{align*} (右辺) &= \frac{2n \sin 2\theta \cdot n \tan 2\theta}{n \sin 2\theta + n \tan 2\theta} \\
\\
&= \frac{2n \sin 2\theta \tan 2\theta}{\sin 2\theta + \tan 2\theta} \\
\\
&= \frac{2n \sin 2\theta \cdot 1}{\frac{\sin 2\theta}{\tan 2\theta} +1} \\
\\
&= \frac{2n \sin 2\theta }{\cos 2\theta +1} \\
\\
&= 2n \cdot \frac{2\sin \theta \cos \theta }{2\cos^2{\theta}-1 +1} \\
\\
&= 2n \cdot \frac{2\sin \theta \cos \theta }{2\cos^2{\theta}} \\
\\
&= 2n \cdot \frac{\sin \theta }{\cos{\theta}} \\
\\
&= 2n \tan \theta
\end{align*} であり、$④$より、$2n \tan \theta = b_{2n}$ となるため、$~\displaystyle b_n = \frac{2a_n b_n}{a_n + b_n}~$が示された。
最後に、$a_{2n} = \sqrt{a_n b_{2n}}$ を示す。
右辺に$①$と$④$を代入すると、
\begin{align*} (右辺) &= \sqrt{n \sin 2\theta \cdot 2n \tan \theta} \\
\\
&= \sqrt{2n^2 \cdot 2\sin \theta \cos \theta \cdot \frac{\sin \theta}{\cos \theta}}\\
\\
& = \sqrt{2^2 \cdot n^2 \sin^2 \theta} \\
\\
&= \sqrt{(2n \sin \theta)^2} \end{align*} となる。
ここで、$~\theta = \displaystyle \frac{90^{\circ}}{n}~$なので、$n \geqq 3$であることから、$\sin \theta > 0$。
したがって、
\sqrt{(2n \sin \theta)^2} = 2n \sin \thetaなので、$③$より、$2n \sin \theta = a_{2n}$。
以上より、$a_{2n} = \sqrt{a_n b_{2n}}~$が示された。$~\blacksquare~$
これで理論上、$~a_n~$と$~b_n~$から無限に、$~a_{2n}~$と$~b_{2n}~$の値を求められるようになりました。
実際に手で計算してみた
アルキメデス同様、正六角形から始めてみます。
円に内接する正六角形と外接する正六角形の周の長さは、以下のように計算されます。
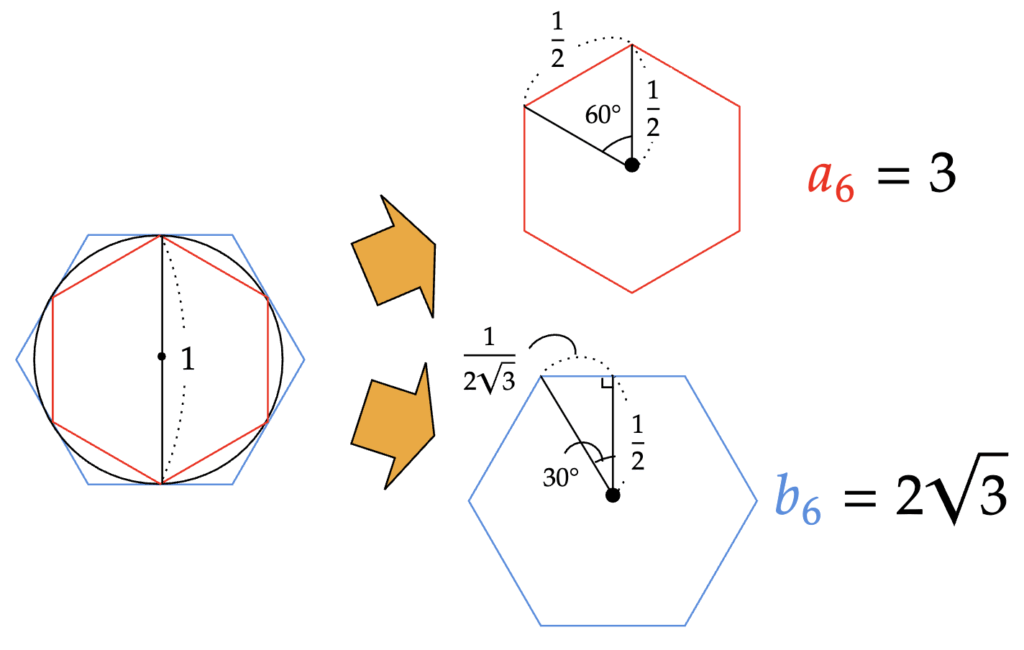
これらの値をもとに$~a_{12}~,~b_{12}~$を計算してみます。
まずは$~b_{12}~$を求める。
\begin{align*}
b_{12}&=\frac{2a_6b_6}{a_6+b_6} \\
\\
&=\frac{2\cdot 3 \cdot 2\sqrt{3}}{3+2\sqrt{3}}
\\
&=\frac{12\sqrt{3}(2\sqrt{3}-3)}{(2\sqrt{3}+3)(2\sqrt{3}-3)} \\
\\
&=\frac{12\sqrt{3}(2\sqrt{3}-3)}{3} \\
\\
&=4\sqrt{3}(2\sqrt{3}-3) \\
\\
&=12(2-\sqrt{3})
\end{align*}この値を利用し、$~a_{12}~$を求める。
\begin{align*}
a_{12}&=\sqrt{a_6b_{12}} \\
\\
&=\sqrt{3\cdot 12(2-\sqrt{3})} \\
\\
&=\sqrt{18\cdot 2(2-\sqrt{3})} \\
\\
&=3\sqrt{2}\sqrt{4-2\sqrt{3}} \\
\\
&=3\sqrt{2}\sqrt{(\sqrt{3}-1)^2} \\
\\
&=3\sqrt{2}(\sqrt{3}-1) \\
\\
&=3(\sqrt{6}-\sqrt{2}) \\
\end{align*}$~\sqrt{2}~,~\sqrt{3}~,~\sqrt{6}~$の近似値を代入することで、以下のように$~a_{12}~,~b_{12}~$が計算される。
a_{12} \fallingdotseq 3.1058~~,~~b_{12} \fallingdotseq 3.2154分母の有理化や二重根号などの計算を行った割には、
3.1058<\pi<3.2154
ということで、正12角形では小数第1位すら求めることができません。
この複雑な計算を、紀元前に正96角形まで行っている時点でアルキメデスの才能がわかります。
実際にコンピュータで計算してみた
正六角形から始めると、以下のように値が求められます。
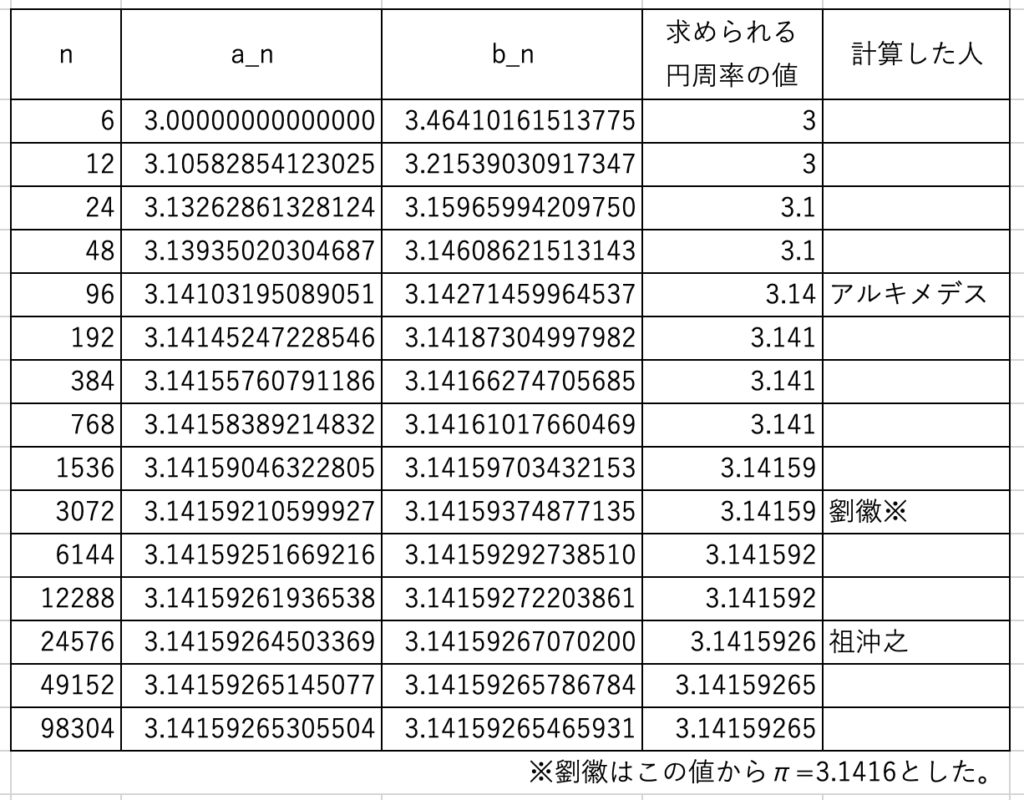
ルドルフの正$~2^{62}~$角形については、正四角形または正八角形から始めたと考えられます。
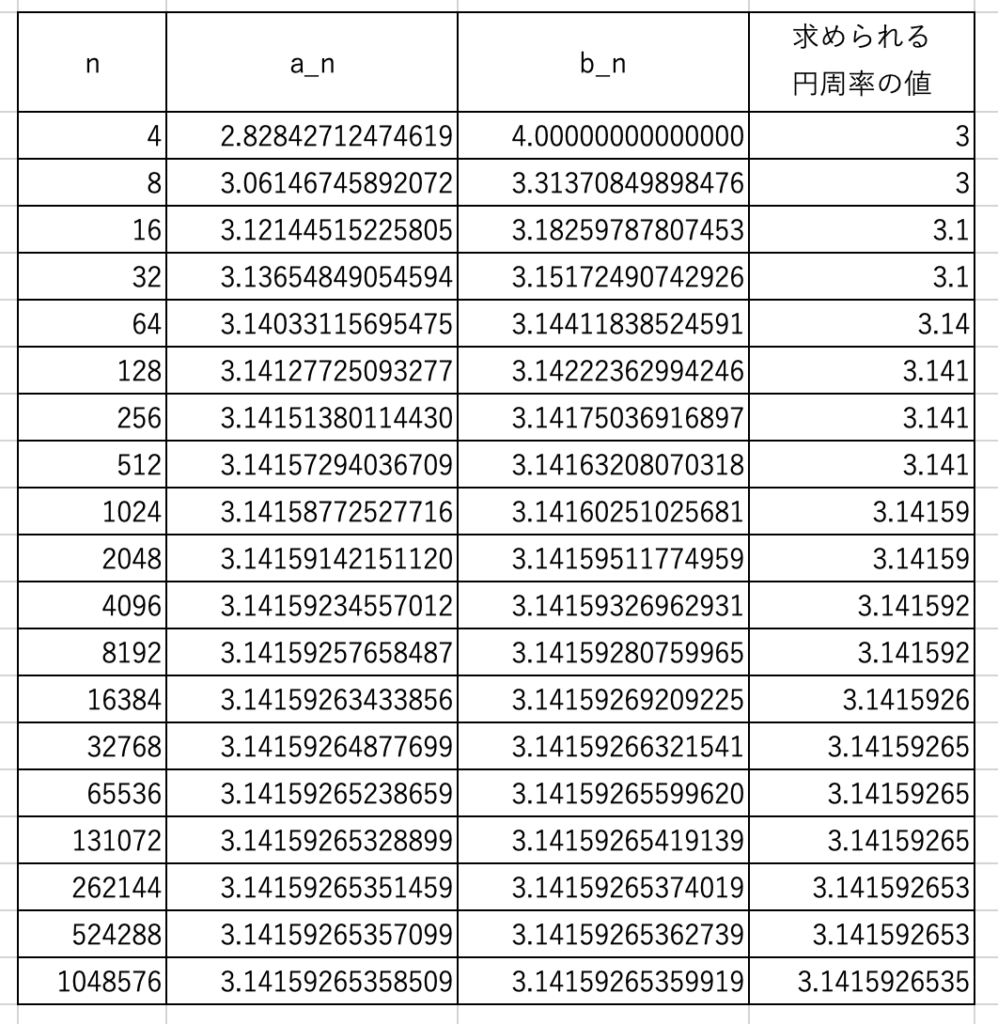
最後の正$~2^{20}~$角形でやっと小数第10位が出てきます。
コンピュータなしで小数第35位まで計算したルドルフは、一生を円周率に捧げたと言われています。

(出典:A.L. Boon, CC BY-SA 3.0, via Wikimedia Commons)
まとめ
円周率の2つの求め方のうち、アルキメデスから始まった正多角形による方法を解説してきました。
- 円周率$~\pi~$の求め方には大きく「正多角形による近似」と「無限級数による計算」という2つの流れがある。
- 紀元前から近世まで、円に内接・外接する正多角形の周の長さを計算し、円周を両側からはさむ方法が使われた。
- 正多角形の辺数が増えるほど$~\pi~$の真値に近づくが、計算量の割に近づくスピードが遅い。

ルドルフ・ファン・ケーレンの円周率に対する想いがわかる計算量・・・。



アルキメデスの時代は、$~\sqrt{~}$の近似値を求めるだけで大変。ルドルフに限らず、各々の時代で使える武器の中で、円周率を求めていたんだ。




コメント