14世紀のヨーロッパでは、古代ギリシャの哲学者アリストテレス以来、長らく停滞していた運動に関する研究が、再び活発になりました。
物がどのように動くのかを数学的に解明しようという試みが始まり、このことが「比の理論」を大きく発展させるきっかけとなりした。
比の理論を発展させた立役者として名前が挙がるのが、トーマス・ブラドワディーンとウォリングフォードのリチャードという二人の数学者。
この記事では、運動学に精通する2人の数学者が、比の理論をどう発展させたかを現役数学教員で数学史の先生であるFukusukeが解説します。
実は、小学校で学ぶ「比の値」は、リチャードによって「デノミナティオ」として与えられたものだったんです！
Fukusuke（ふくすけ）
数学史の先生
- 現役の中学・高校数学教員
- 著書2冊
重刷、ブログ累計200万PV達成 - 行間がなくなるほど丁寧な式変形で執筆中
Fukusuke（ふくすけ）
数学史の先生
- 現役の中学・高校数学教員
- 著書2冊は発売1ヶ月で即重刷
- 当数学史ブログは累計200万PV達成
- 行間がなくなるほど丁寧な式変形で記事を執筆
『世界を変えた数学史図鑑』『教養としての数学史』好評発売中！
読みやすいと好評です！
読みやすいと好評です！
なぜ中世で比が発展したのか？
中世ヨーロッパで比の理論が大きく発展した背景には、運動を数学的に記述しようとする「運動学」の流行がありました。
運動学が盛んだったから
14世紀、ヨーロッパの大学では、物体の運動を記述し、その速さや距離、時間の関係を数式で表そうとする研究が盛んになりました。
それまではアリストテレスの物理学が絶対的な権威を持っていましたが、学者たちはその理論だけでは説明できない現象に気づき始めたのです。
アリストテレス物理学と中世以降（主にガリレオ以降の物理学）の違いのイラスト
特に、加速度運動（だんだん速くなる運動）の記述は大きな課題でした。
この課題に取り組む中で、速さの変化の「割合」や、力と抵抗の「比」といった概念が重要視されるようになり、比の理論が深く探求されることになりました。
中世ヨーロッパにおける運動学と比の理論の発展を年表でまとめると、以下の通りです。
| 年代 | 人物 | 功績 |
|---|---|---|
| 13世紀前半 | ヨルダヌス・ネモラリウス | 静力学の研究で知られ、後の運動学研究の基礎を築いたとされる。 |
| 1290年～1349年 | トーマス・ブラドワディーン | アリストテレスの運動法則を修正し、速さは力と抵抗の比の対数に比例すると提唱した（誤りではあったものの、運動学を数学的モデルで考えるきっかけになった） |
| 1292年～1336年 | ウォリングフォードのリチャード | ブラドワディーンの同僚。「デノミナティオ」という現在の比の値を使って、比の合成を分数の乗法として明確に定義した。 |
| 1320年～1382年 | ニコル・オレーム | 運動の様子をグラフ化した。比の性質を利用し、等加速度運動における時間と距離の関係に気づいた。 |
14世紀のオックスフォード中心に研究された
この運動学研究の中心地となったのが、イギリスのオックスフォード大学、特にマートン学寮（Merton College）でした。
ここに集った優秀な学者たちは「マートン学派」と呼ばれ、互いに議論を重ねながら、運動に関する新しい理論を次々と生み出していきました。
その中でも特に有名なのが「マートン規則」です。
一様に加速する物体の平均速度は、初速度と最終速度の算術平均に等しい。
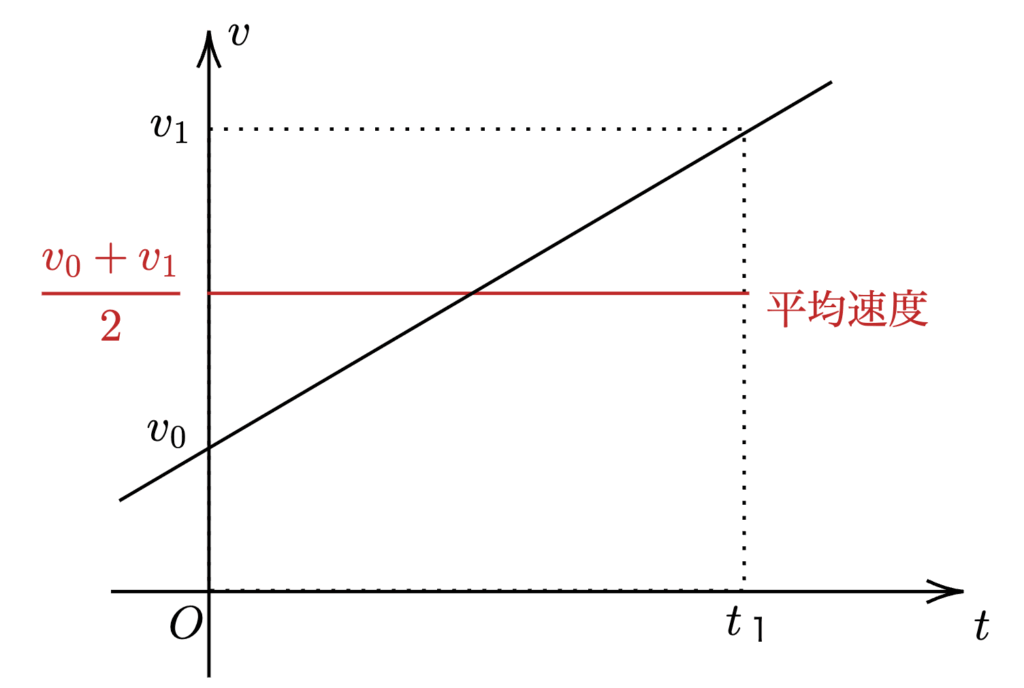
実際に運動の様子をグラフで表し始めたのは、少し後のフランスの数学者ニコル・オレームで、彼への橋渡しとなったマートン学派の数学者がブラドワディーンとリチャードだったのです。
トーマス・ブラドワディーンとは？
トーマス・ブラドワディーンは、マートン学派を代表する最も重要な人物の一人です。
「深遠博士」の異名を持つ数学者
トーマス・ブラドワディーン（Thomas Bradwardine , 1290年-1349年）は、オックスフォード大学の神学教授でありながら、数学と物理学に深い関心を寄せていました。
その学識の深さから「深遠博士（Doctor Profundus）」という異名で呼ばれるほど、当時の学者たちから尊敬を集めていました。
ブラドワディーンは以下のような生涯を送っています。
| 年代 | 出来事 |
|---|---|
| 1290頃 | ハートフィールドに生まれる |
| (不明) | オックスフォード大学マートン学寮で学ぶ |
| 1328 | 『比の理論』を執筆 |
| (不明) | セント・ポール大聖堂の主席司祭となる |
| 1349 | オックスフォードにて没 |
彼は後にカンタベリー大司教というキリスト教世界の最高位にまで上り詰めますが、その生涯を通じて数学の研究を続け、『算術考察』や『幾何学考察』といった専門書も著しています。
アリストテレスの運動規則を定式化した
ブラドワディーンの最大の功績は、アリストテレスの運動法則を修正し、より精密な数式で表現したことです。
アリストテレスは、以下のように運動法則を考えていました。
速さ$~V~$は力$~F~$に比例し、抵抗$~R~$に反比例する。
すなわち、$~K~$を定数として、
V=\frac{KF}{R}と表される。
しかしこの法則では、力が抵抗と等しい場合も物体が動いてしまいます。
ブラドワディーンは1328年の著作『比の理論』で、以下のように主張しました。
速さ$~V~$は力$~F~$の対数に比例し、抵抗$~R~$に対して、対数的に減少する。
すなわち、$~K~,~a~$を比例定数として、
V = K \log_a\left(\frac{F}{R}\right)と表される。
ブラドワディーンは上記のように対数を使った訳ではなく、速さを2倍するには、力と抵抗の比（の値）を2乗する必要があると説明しました。
しかし、ブラドワディーンの法則であれば、力と抵抗が等しい場合は速さが$~V=K\log_a{1}=0~$となりため、アリストテレスの法則よりも正確さが増していることがわかります。
比例論を一般化した
数学史的に、ブラドワディーンの運動法則がもたらしたのは、比の理論の発展です。
$~V = K \log_a\left(\frac{F}{R}\right)~$のとき、速さを$~2~$倍、$~3~$倍、$~\displaystyle \frac{1}{2}~$倍、$~\displaystyle \frac{1}{3}~$倍するためには、次のように力と抵抗の比の値$~\left( \displaystyle\frac{F}{R}~\right)~$を$~2~$乗、$~3~$乗、$~\displaystyle \frac{1}{2}~$乗、$~\displaystyle \frac{1}{3}~$乗すればよい。
\begin{align*}
2V&=2K \log_a\left(\frac{F}{R}\right)=K \log_a\left(\frac{F}{R}\right)^2 \\
\\
3V&=3K \log_a\left(\frac{F}{R}\right)=K \log_a\left(\frac{F}{R}\right)^3 \\
\\
\frac{1}{2}V&=\frac{1}{2}K \log_a\left(\frac{F}{R}\right)=K \log_a\left(\frac{F}{R}\right)^{\frac{1}{2}} \\
\\
\frac{1}{3}V&=\frac{1}{3}K \log_a\left(\frac{F}{R}\right)=K \log_a\left(\frac{F}{R}\right)^{\frac{1}{3}} \\
\\
\end{align*}ブラドワディーンは、それまで比を表すための関係でしかなかった分数（後述のリチャードが「デノミナティオ（比の値）」と定義）を計算対象として扱い、比の「$~n~$乗」や「$~n~$乗根」という考え方を導入したのです。
このことは、比で扱える数の範囲が広がったことを意味しています。
ブラドワディーンの理論も間違っていた
現在知られているように、現代のニュートン力学では、力や抵抗によって決まるのは速度ではなく加速度です。
F=ma
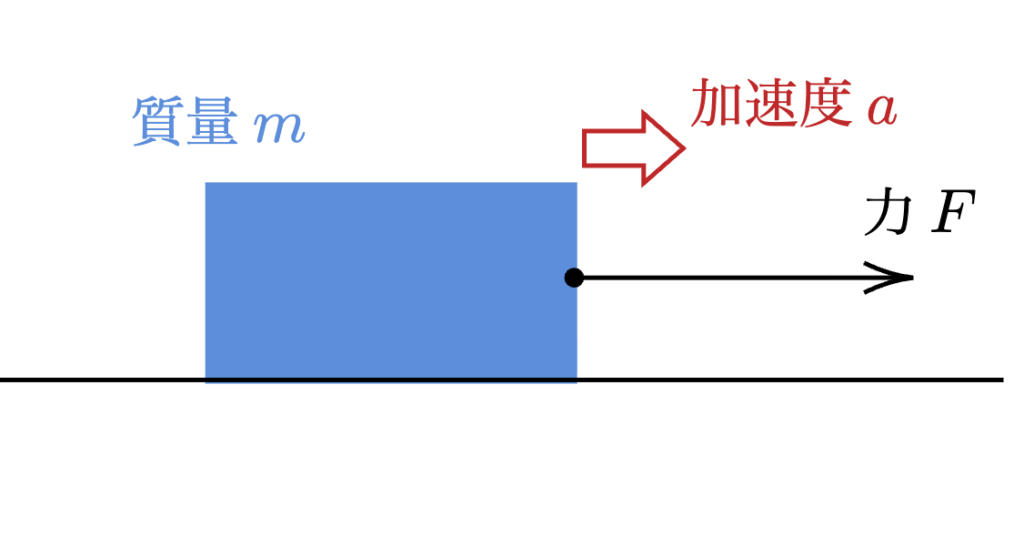
ブラドワディーンの理論は間違っていたものの、彼の理論はアリストテレスの単純な比例関係から脱却し、運動という物理現象を、より複雑な数学的関数（対数関数）で表現しようとした最初の試みとなりました。
近代科学の基本的な姿勢の先駆けとなったのです。
ウォリングフォードのリチャードとは？
ブラドワディーンの研究を数学的に支えたのが、同僚であったウォリングフォードのリチャードです。
ブラドワディーンの同僚の数学者
ウォリングフォードのリチャード（Richard of Wallingford , 1292年頃〜1336年）も、ブラドワディーンと同じくオックスフォード大学マートン学寮の数学者です。
ウォリングフォードというのは、イングランド南部の町の名前です。
リチャードは以下のような生涯を送っています。
| 年代 | 出来事 |
|---|---|
| 1292頃 | 生まれる |
| (不明) | オックスフォード大学マートン学寮で学ぶ |
| (不明) | 『四部作』を執筆 |
| 1336 | 亡くなる |
リチャードはブラドワディーンの運動理論に数学的な厳密さを与えるため、比の理論の基礎を徹底的に見直しました。
彼の研究は、ブラドワディーンの運動法則が感覚的な推論だけでなく、しっかりとした数学的土台に基づいていることを示す上で不可欠な役割を果たしました。
比の値（デノミナティオ）を定義した
リチャードの貢献を理解する上で鍵となるのが「デノミナティオ（denominatio）」という概念です。
これは、現代語に訳せば「比の値」や「名称を与えるもの」といった意味になります。
比とは、同種の量二つの間にある関係である。
比で、一方が他方を割るとき、その結果をデノミナティオという。
リチャードは、古代ギリシャから扱われてきた2つの量の関係を表す「比」を再定義しつつ、その比から生じる数を新たに定義しました。
その数こそ、現在の「比の値」にあたるデノミナティオです。
リチャードは$~3:1~$という比に対するデノミナティオとして「3倍比」という名称を使い、$~1:3~$という比に対するデノミナティオとして「3分比」という名称を使っています。
ブラドワディーンの運動法則を考えるために必要不可欠な「比の値」を、「デノミナティオ」として定義することで、研究をしやすくしました。
デノミナティオで比の合成を明確化した
リチャードの功績は、著作『四部作』の中で、このデノミナティオの概念を用いて「比の合成」を明確に定義したことです。
デノミナティオの積が、あるデノミナティオを生じるとき、比と比が合成されたという。
デノミナティオの商がデノミナティオを生じるとき、比が比によって割られたという。
彼は現在でも行われる比の合成を、上記のデノミナティオの積や商から求める方法を示しています。
$~1:4~$と$~8:1~$を合成する場合、
- $~1:4~$のデノミナティオは、「$~4~$分比」
- $~8:1~$のデノミナティオは、「$~8~$倍比」
上記の2つのデノミナティオの積は$~\displaystyle \frac{1}{4} \times 8=2~$であることから、$~1:4~$と$~8:1~$を合成した比のデノミナティオは「$~2~$倍比」。
したがって、最も簡単な整数比で表した場合の合成比は$~2:1~$である。
古代ギリシャのユークリッドも線分の連結的配置や重ね合わせに基づいて「比の合成」を行なっていたものの、リチャードの定義のほうが格段にわかりやすく、現代数学から見ても正しいものです。
このおかげで、ブラドワディーンの複雑な運動法則も、数学的にスムーズに扱えるようになりました。
まとめ
この記事では、中世ヨーロッパにおける比の理論の発展を、トーマス・ブラドワディーンとウォリングフォードのリチャードという二人の数学者の功績を中心に解説しました。
- 14世紀のオックスフォード大学マートン学寮を中心に、運動を数学的に記述しようとする研究が盛んになった
- ブラドワディーンはアリストテレスの運動法則を修正し、速さと力・抵抗の関係を対数関数で表現した。
- ウォリングフォードのリチャードは、ブラドワディーンの理論を数学的に支えるため、「デノミナティオ」という概念を導入した
マートン学派の数学者がブラドワディーンとリチャードは、実際に運動の様子をグラフで表し始めたフランスの数学者、ニコル・オレームへの橋渡しとなったのです。
コメント