円に内接する四角形の面積を求める「ブラーマグプタの公式」は、次のような公式で与えられます。
S=\sqrt{(s-a)(s-b)(s-c)(s-d)}4辺の長さだけで面積を計算できる画期的な公式であり、三角形の面積を求めるヘロンの公式を四角形に拡張したものとして知られています。
この記事では、ブラーマグプタの公式の証明方法を3種類紹介！
公式の使い方やインドの数学者ブラーマグプタの勘違いについても、数学史の先生Fukusukeがていねいにわかりやすく解説します。
Fukusuke（ふくすけ）
数学史の先生
- 現役の中学・高校数学教員
- 著書2冊
重刷、ブログ累計200万PV達成 - 行間がなくなるほど丁寧な式変形で執筆中
Fukusuke（ふくすけ）
数学史の先生
- 現役の中学・高校数学教員
- 著書2冊は発売1ヶ月で即重刷
- 当数学史ブログは累計200万PV達成
- 行間がなくなるほど丁寧な式変形で記事を執筆
『世界を変えた数学史図鑑』『教養としての数学史』好評発売中！
丸善日本橋店の2025年ベストセラー（理工書部門）に選ばれました！
（理工書部門）に選ばれました！
ブラーマグプタの公式とは？
ブラーマグプタの公式は、円に内接する四角形の面積を、4辺の長さだけを使って求めることができる画期的な公式です。
この公式を使えば、複雑な計算をすることなく、四角形の面積を簡単に知ることができます。
円に内接する四角形の面積を求められる
ブラーマグプタの公式は、四角形が円に内接するという特別な場合にのみ利用できます。
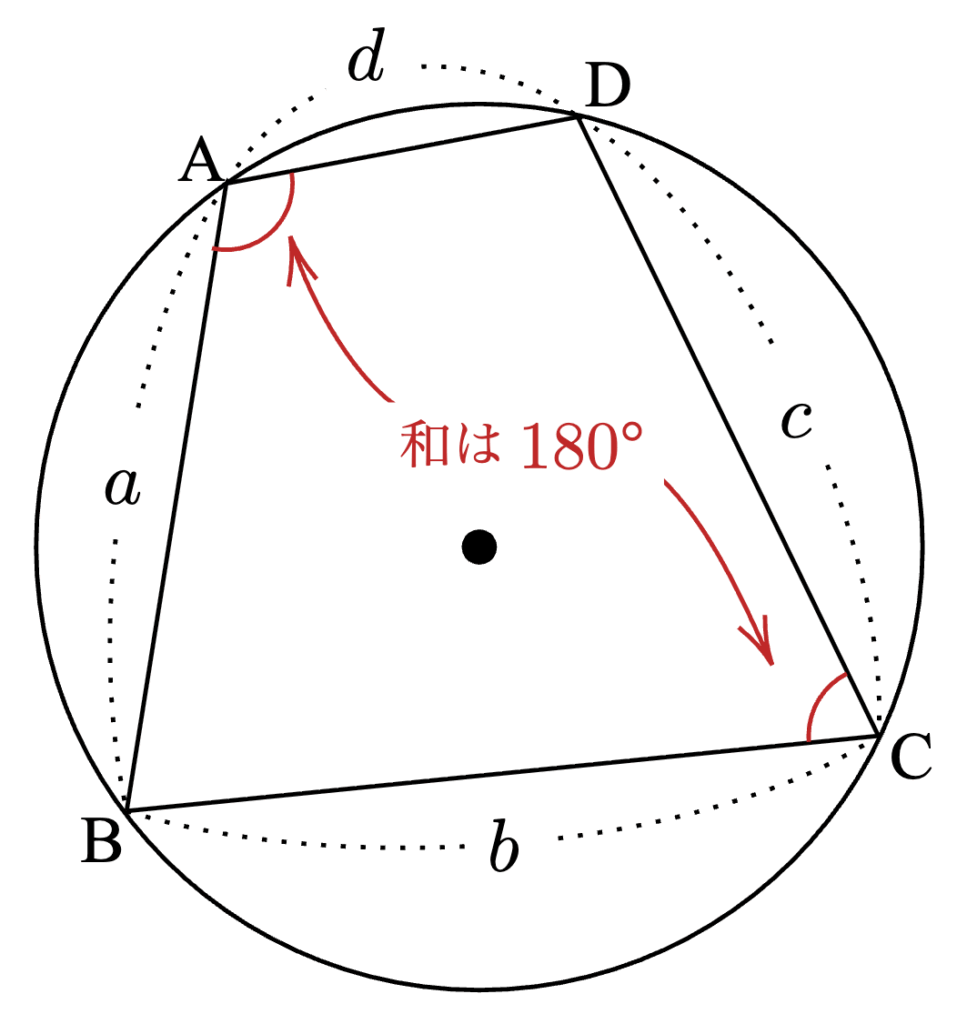
4つの辺の長さが、$~a~,~b~,~c~,~d~$の円に内接する四角形$~ABCD~$で、
s=\frac{a+b+c+d}{2}とする。
このとき、四角形$~ABCD~$の面積$~S~$は次のように求めることができる。
S=\sqrt{(s-a)(s-b)(s-c)(s-d)}この公式は、三角形の面積を3辺の長さから求めるヘロンの公式を四角形に拡張したものと考えることができます。
実際、四角形の辺の1つの長さ $d$ を0に近づけると、この公式はヘロンの公式と一致します。
逆に、「円に内接する」という条件をとった面積公式がブレートシュナイダーの公式です。
数学Ⅰで出てくる問題例
ブラーマグプタの公式は、高校の数学Ⅰの教科書や大学入試問題でも別解として登場します。
例えば、次のような問題を見てみましょう。
円に内接する四角形$~ABCD~$があり、$~AB=2, BC=3, CD=4, DA=5~$ とする。
この四角形の面積$~S~$を求めなさい。
まず、半周長 $s$ を計算する。
s = \frac{2+3+4+5}{2} = 7次に、ブラーマグプタの公式に値を代入すると、面積が求められる。
\begin{align*}
S &= \sqrt{(7-2)(7-3)(7-4)(7-5)} \\
&= \sqrt{5 \cdot 4 \cdot 3 \cdot 2} \\
&= \sqrt{120} \\
&= 2\sqrt{30}
\end{align*}このように、公式を知っていれば、辺の長さだけで簡単に面積を求めることができます。
教科書に載っている一般的な解法の場合、以下のようになります。
対角線$~BD~$をひく。
$~\angle A=\theta~$とおくと、円に内接する四角形の性質から$~\angle C=180^{\circ}-\theta~$と表せる。
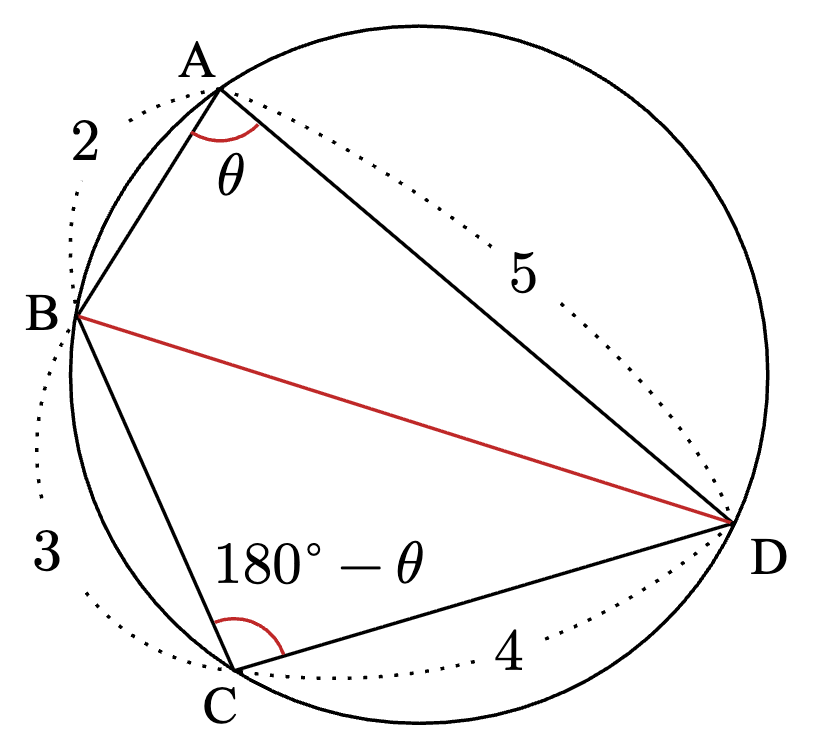
$~\triangle ABD~$で余弦定理を使うと、
\begin{align*}
BD^2 &= 2^2+5^2-2\cdot 2\cdot 5\cdot \cos{\theta} \\
&=29-20\cos{\theta}~~~\cdots ①
\end{align*}であり、$~\triangle CBD~$で余弦定理を使うと、
\begin{align*}
BD^2 &= 3^2+4^2-2\cdot 3\cdot 4\cdot \cos{(180^{\circ}-\theta)} \\
&=25-24(-\cos{\theta}) \\
&=25+24\cos{\theta} ~~~\cdots ②
\end{align*}である。
$①$、$②$より、
\begin{align*}
29-20\cos{\theta}&=25+24\cos{\theta} \\
-44\cos{\theta}&=-4 \\
\cos{\theta}&=\frac{1}{11} \\
\end{align*}であるため、$~\sin^2{\theta}+\cos^2{\theta}=1~$より、
\begin{align*}
\sin^2{\theta}+\frac{1}{121}&=1 \\
\\
\sin^2{\theta}&=\frac{120}{121} \\
\\
\sin{\theta}&=\frac{2\sqrt{30}}{11} ~~~~~(\because~0^{\circ}<\theta<180^{\circ})\\
\end{align*}が求められる。
したがって、四角形$~ABCD~$の面積$~S~$は、三角形の面積公式により、
\begin{align*}
S&=\triangle ABD+\triangle CBD \\
&=\frac{1}{2}\cdot 2 \cdot 5 \cdot \sin{\theta}+\frac{1}{2}\cdot 3 \cdot 4 \cdot \sin{(180^{\circ}-\theta)} \\
&= \frac{1}{2}\cdot 2 \cdot 5 \cdot \sin{\theta}+\frac{1}{2}\cdot 3 \cdot 4 \cdot \sin{\theta}\\
&=11\sin{\theta} \\
&=11\cdot \frac{2\sqrt{30}}{11} \\
&=2\sqrt{30}
\end{align*}と求めることができた。
誘導問題として$~AC~$の長さや$~\angle B~$の大きさを求めることもありますが、四角形の面積を求めるだけであれば、ブラーマグプタの公式の有用性がよくわかります。
発見者と証明者は違う人
この公式を発見したのは、7世紀にインドで活躍した数学者・天文学者のブラーマグプタ（Brahmagupta , 598年～668年頃）です。
（出典：https://mathshistory.st-andrews.ac.uk/Biographies/Brahmagupta/pictdisplay/）
彼は自身の著書『ブラーフマスプタシッダーンタ』（628年）の中でこの公式を発表しました。
しかし、ブラーマグプタ自身は、この公式が「円に内接する四角形」という特別な場合にのみ成り立つことには気づいていなかったとされています。
彼が発見した公式の厳密な証明は、イスラムの数学者アル・ビールーニー（Al-Biruni , 973〜1048）をはじめとする後世の数学者たちによって与えられました。
（出典：The original uploader was Romanm at Slovenian Wikipedia., Public domain, via Wikimedia Commons）
つまり、公式の「発見者」と「証明者」は異なる人物なのです。
ブラーマグプタの公式の3通りの証明
ブラーマグプタの公式には、いくつかの証明方法が存在します。
ここでは、その中でも3つの証明方法を紹介します。
余弦定理による証明
この証明は、先ほどの教科書的な解法を一般化したもの。
四角形を2つの三角形に分割し、それぞれの面積を三角比と余弦定理を用いて表すことから始まります。
対角線$~BD~$をひく。
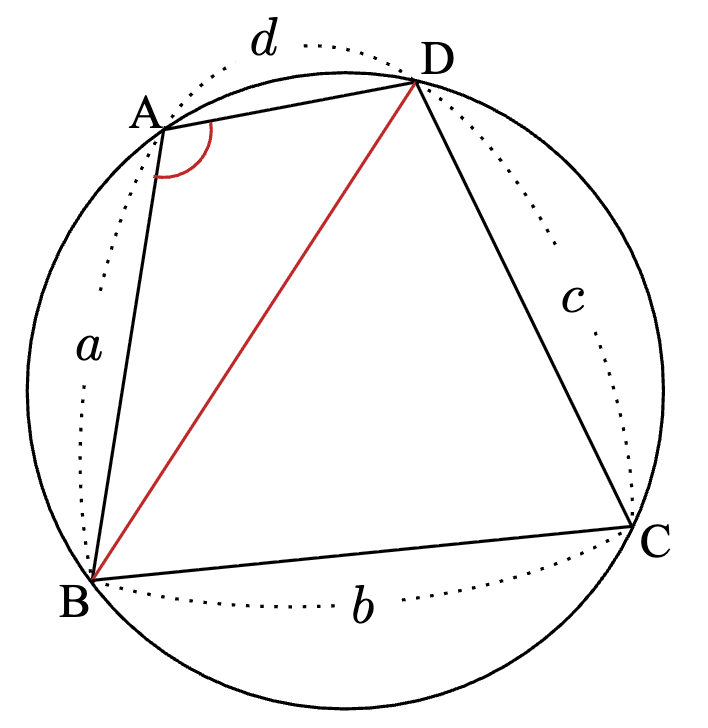
四角形$ABCD$の面積を$~S~$とすると、
\begin{align*}
S&=\triangle ABD+\triangle CBD \\
&=\frac{1}{2}ad\sin{A}+\frac{1}{2}bc\sin{C}\cdots①
\end{align*}四角形$~ABCD~$は円に内接するため、対角の和は$~180^{\circ}~$。
よって、
\sin{C}=\sin{(180^{\circ}-A)}=\sin{A}①に代入することで
\begin{align*}
S&=\frac{1}{2}ad\sin{A}+\frac{1}{2}bc\sin{A} \\
&=\frac{1}{2}(ad+bc)\sin{A}\cdots②
\end{align*}となる。
②の両辺を2乗し、
\begin{align*}
S^2&=\frac{1}{4}(ad+bc)^2\sin^2{A} \\
&=\frac{1}{4}(ad+bc)^2(1-\cos^2{A})\cdots③
\end{align*}となる。
ここで、$~\triangle ABD~$で余弦定理を使うと、
BD^2 = a^2 + d^2 - 2ad\cos{A}また、$~\triangle CBD~$で余弦定理を使うと、
\begin{align*}
BD^2 &= b^2 + c^2 - 2bc\cos{A} \\
&= b^2 + c^2 - 2bc\cos{(180^{\circ}-A)} \\
&= b^2 + c^2 + 2bc\cos{A}
\end{align*}なので、
\begin{align*}
a^2 + d^2 - 2ad\cos{A}&=b^2 + c^2 + 2bc\cos{A}\\
2ad\cos{A} + 2bc\cos{A}&= a^2 + d^2 - b^2 - c^2\\
\cos{A} &= \frac{a^2 + d^2 - b^2 - c^2}{2(ad + bc)}\\
\cos^2{A}&= \frac{(a^2 + d^2 - b^2 - c^2)^2}{4(ad + bc)^2} \cdots④\\
\end{align*}が求まる。
$~④~$を$~③~$に代入すると、
\begin{align*}
S^2 &= \frac{1}{4}(ad+bc)^2\left\{1-\frac{(a^2+d^2-b^2-c^2)^2}{4(ad+bc)^2}\right\} \\
&= \frac{1}{4}(ad+bc)^2 - \frac{(a^2+d^2-b^2-c^2)^2}{16} \\
&= \frac{1}{16}\left\{4(ad+bc)^2-(a^2+d^2-b^2-c^2)^2\right\} \\
&= \frac{1}{16}\left\{2(ad+bc)+(a^2+d^2-b^2-c^2)\right\}\left\{2(ad+bc)-(a^2+d^2-b^2-c^2)\right\} \\
&= \frac{1}{16}\left(2ad+2bc+a^2+d^2-b^2-c^2\right)\left(2ad+2bc-a^2-d^2+b^2+c^2\right) \\
&= \frac{1}{16}\left\{(a^2+2ad+d^2)-(b^2-2bc+c^2)\right\}\left\{(b^2+2bc+c^2)-(a^2-2ad+d^2)\right\} \\
&= \frac{1}{16}\left\{(a+d)^2-(b-c)^2\right\}\left\{(b+c)^2-(a-d)^2\right\} \\
&= \frac{1}{16}\{(a+d)+(b-c)\}\{(a+d)-(b-c)\}\{(b+c)+(a-d)\}\{(b+c)-(a-d)\} \\
&= \frac{1}{16}(a+b+c+d-2c)(a+b+c+d-2b)(a+b+c+d-2d)(a+b+c+d-2a) \\
&= \left(\frac{a+b+c+d}{2}-c\right)\left(\frac{a+b+c+d}{2}-b\right)\left(\frac{a+b+c+d}{2}-d\right)\left(\frac{a+b+c+d}{2}-a\right) \\
&= (s-a)(s-b)(s-c)(s-d)
\end{align*}なので、
S = \sqrt{(s-a)(s-b)(s-c)(s-d)}が求まる。
式変形は複雑なものの、高校数学の知識で理解できる、最も基本的な証明方法でした。
ヘロンの公式による証明
この証明は、少しトリッキーですが非常にエレガントな方法です。
直線$~DA~$と直線$~BC~$の交点を$~P~$とする。
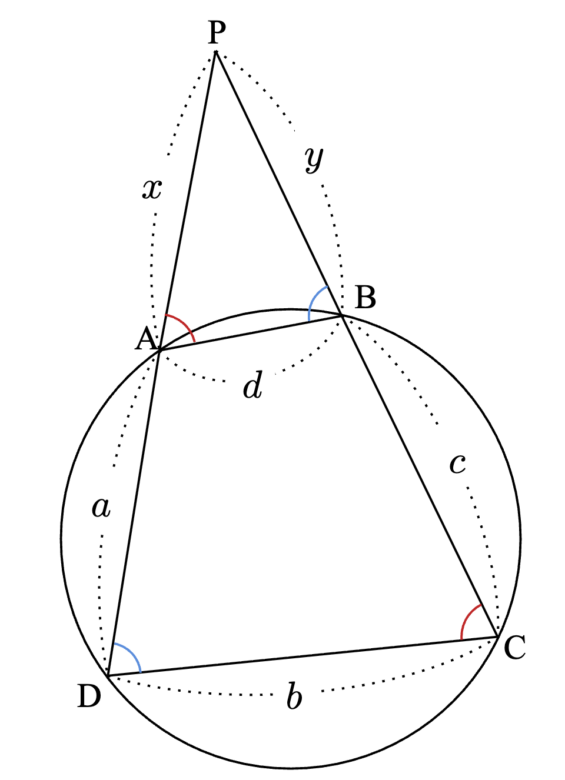
円に内接する四角形において、1つの内角はその対角の外角と等しいので、
\angle PDC = \angle PBA, ~\angle PCD = \angle PAB
となる。
したがって、三角相等より$~\triangle PCD~$∽$~\triangle PAB~$なので、$~PA = x~$、$~PB = y~$とすると、
\begin{cases}
c : a = (y+b) : x \\
c : a = (x+d) : y
\end{cases}
から、
\begin{cases}
a(y+b) = cx \cdots ①\\
a(x+d) = cy \cdots ②
\end{cases}となる。
$~①+②~$より、
\begin{align*}
ay + ab + ax + ad &= cx + cy \\
ax - cx + ay - cy &= -ab - ad \\
(a-c)x + (a-c)y &= -a(b+d) \\
(a-c)(x+y) &= -a(b+d) \\
x+y &= -\frac{a(b+d)}{a-c} \\
x+y &= \frac{a(b+d)}{c-a} \cdots ③
\end{align*}となり、$~①-②~$より、
\begin{align*}
ay + ab - ax - ad &= cx - cy \\
ay + cy - ax - cx &= -ab + ad \\
(a+c)y - (a+c)x &= -a(b-d) \\
-(a+c)(x-y) &= -a(b-d) \\
x-y &= \frac{a(b-d)}{a+c} \cdots ④
\end{align*}となる。
ここで、$~\triangle PCD~$と$~\triangle PAB~$の面積を考えると、相似な三角形の面積比は相似比の2乗。
\begin{align*}
\triangle PCD : \triangle PAB &= c^2 : a^2\\
a^2 \triangle PCD &= c^2 \triangle PAB\\
a^2(\triangle PAB + S) &= c^2 \triangle PAB\\
a^2 \triangle PAB + a^2 S &= c^2 \triangle PAB\\
a^2 S &= (c^2 - a^2) \triangle PAB\\
S &= \frac{c^2 - a^2}{a^2} \triangle PAB \cdots ⑤
\end{align*}$~\triangle PAB~$について、ヘロンの公式より、
t = \frac{a + x + y}{2}\cdots⑥とすると、
\triangle PAB = \sqrt{t(t-a)(t-x)(t-y)}なので、$~⑥,③,④~$を代入すると、
\begin{align*}
\triangle PAB &= \sqrt{\left(\frac{a+x+y}{2}\right)\left(\frac{-a+x+y}{2}\right)\left(\frac{a-x+y}{2}\right)\left(\frac{a+x-y}{2}\right)} \\
&= \frac{1}{4}\sqrt{(a+x+y)(-a+x+y)\{a-(x+y)\}(a+x-y)} \\
&= \frac{1}{4}\sqrt{\left\{a+\frac{a(b+d)}{c-a}\right\}\left\{-a+\frac{a(b+d)}{c-a}\right\}\left\{a-\frac{a(b-d)}{a+c}\right\}\left\{a+\frac{a(b-d)}{a+c}\right\}} \\
&= \frac{1}{4}\sqrt{a^4\frac{c-a+b+d}{c-a} \cdot \frac{-(c-a)+b+d}{c-a} \cdot \frac{a+c-(b-d)}{a+c} \cdot \frac{a+c+b-d}{a+c}} \\
&= \frac{a^2}{4}\sqrt{\frac{-a+b+c+d}{c-a} \cdot \frac{a+b-c+d}{c-a} \cdot \frac{a-b+c+d}{a+c} \cdot \frac{a+b+c-d}{a+c}} \cdots ⑦
\end{align*}である。
最後に$~⑦~$を$~⑤~$に代入して、
\begin{align*}
S &= \frac{(c+a)(c-a)}{a^2} \cdot \frac{a^2}{4}\sqrt{\frac{-a+b+c+d}{c-a} \cdot \frac{a+b-c+d}{c-a} \cdot \frac{a-b+c+d}{a+c} \cdot \frac{a+b+c-d}{a+c}} \\
&= \frac{1}{4}\sqrt{(-a+b+c+d)(a+b-c+d)(a-b+c+d)(a+b+c-d)} \\
&= \sqrt{\left(\frac{a+b+c+d}{2}-a\right)\left(\frac{a+b+c+d}{2}-c\right)\left(\frac{a+b+c+d}{2}-b\right)\left(\frac{a+b+c+d}{2}-d\right)} \\
&= \sqrt{(s-a)(s-c)(s-b)(s-d)}
\end{align*}と求まる。$~\blacksquare~$
相似な三角形の性質とヘロンの公式を利用して、鮮やかに公式を導き出す方法でした。
ブレートシュナイダーの公式による証明
ブレートシュナイダーの公式は、円に内接するという条件を持たない、より一般的な四角形の面積を求める公式です。
四角形$~ABCD~$において、$~AB = a~$、$~BC = b~$、$~CD = c~$、$~DA = d~$のとき、
\angle A + \angle C = \theta~,~ s = \frac{a+b+c+d}{2}とおくと、四角形$~ABCD~$の面積を$~S~$は、次のように求まる。
S = \sqrt{(s-a)(s-b)(s-c)(s-d) - abcd\cos^2\frac{\theta}{2}}この公式から、四角形が円に内接するという条件を加えることで、ブラーマグプタの公式が特殊な場合として導かれることを示します。
四角形$~ABCD~$が円に内接するとき、
\theta=\angle A+\angle C =180^{\circ}である。
これをブレートシュナイダーの公式に代入することで、
\begin{align*}
S &= \sqrt{(s-a)(s-b)(s-c)(s-d) - abcd\cos^2{90^{\circ}}} \\
&= \sqrt{(s-a)(s-b)(s-c)(s-d) - abcd\cdot 0^2} \\
&= \sqrt{(s-a)(s-b)(s-c)(s-d) } \\
\end{align*}とブラーマグプタの公式が求められた。$~\blacksquare~$
より広い視点からブラーマグプタの公式を捉えることができる証明方法でした。
まとめ
円に内接する四角形の面積を求める「ブラーマグプタの公式」について解説してきました。
- ブラーマグプタの公式は円に内接する四角形の面積を4辺の長さから求められる
- 7世紀のインドの数学者ブラーマグプタが発見したが、証明はアル・ビールーニーなどが行った
- 余弦定理、ヘロンの公式、ブレートシュナイダーの公式による3通りの証明方法がある
- ヘロンの公式の上位版、ブレートシュナイダーの公式の下位版に位置付けられる。
一口に「ブラーマグプタの公式の証明」といっても、いろんなアプローチのしかたがあるね。
証明がなく、正しい理解ではなかったにも関わらず、ブラーマグプタの名が公式についているってすごいよね。
コメント
コメント一覧 （4件）
お返事頂き、ありがとうございます。
最初、『ブラーマグプタの公式の証明』と検索したところ最上位に『高校数学の美しい物語』というサイトが出てきたので拝見したのですが、証明のはずなのに公式に行き着く式の過程が省略されていたため理解に至らなかったので、こちらの『数学めも』にたどり着き何とか理解する事が出来ました。感謝します。
今後も優先的に参考にさせて頂きます。
学び直し中様
途中式を丁寧に書くことを意識して記事を作成していたため、それがお役に立てて大変嬉しく思えます。
ただ、その分必然的に式の量が増えるので、今回のように式のミスをご指摘いただけるのは大変ありがたいです。
今後ともお役に立てるサイトを作っていくことを目指しますので、またご活用いただける機会がありましたら、どうぞよろしくお願いします。
Fukusuke
はじめまして。
こちらのブラーマグプタの証明についてのご説明、非常に勉強になりました。感謝します。
読み進んで行く内に表記間違いかも知れないと気付いた部分が有り、解りやすく有用な情報なのに勿体ないと思いましたので、以下に当該部分を記させて頂きます。
●ヘロンの公式による説明の部分の前半
①内接四角形の図においてＢとＤを逆にする、②内接四角形の上辺をa、下辺をcとするとその後の説明で辻褄が合う事から、Aを始点とする文字振りを右回りとすべきところ左回りにしてしまったのかなと考えました。
●同じく、ヘロンの公式による説明の部分の後半の『最後に ⑦ を ⑤ に代入して、S=(C²−A²)(CｰA)／ａ²・・・』の部分の『(C²−A²)』は、『(C+A)』かなと考えました。
勉強中の身なので、間違えているかも知れませんが、その際はご容赦願います。
学び直し中様
コメントいただきありがとうございます。
ご丁寧にお読みいただき、また詳細なご指摘をお寄せくださりありがとうございます。
ご指摘いただいた2点についてですが、いずれにつきましても、ご指摘の通りでした。
確認したところ、前者は図と文字の対応関係に誤りがあり、後者は単純な表記ミスでした。
すでにブログ本文および該当箇所の数式・図を修正しております。
このように注意深く読んでいただけることは、書き手として大変ありがたく、励みになります。改めて感謝申し上げます。
今後ともお気づきの点がありましたら、遠慮なくお知らせください。
Fukusuke