三平方の定理の証明は、紀元前からあらゆる人があらゆる方法で考え出してきました。
2023年4月、アメリカの10代の少女2人が新たな証明方法を発見したことがニュースになっています。
しかもこの少女たちは、循環論法になるため避けられてきた三角比を使って証明しました。
この記事では、今回発見された三角比による証明方法をわかりやすく解説すると共に、三角比による方法がなぜ避けられてきたのかを現役教員が解説!
確かに循環論法にはなっておらず、等比級数を最終的には利用した証明方法となります。
三角比を使った証明の難しさ
今回発見された証明方法は、三角比($~\sin{}~$,$~\cos{}~$)を用いたものです。
三平方の定理の証明で三角比を使うのはなぜ難しく、避けられてきたのでしょうか?
三角比の性質の証明に三平方の定理を使う
三角比で出てくる公式の多くは、三平方の定理を使って証明されます。
例を2つほど挙げてみましょう。
\sin^2{A}+\cos^2{A}=1
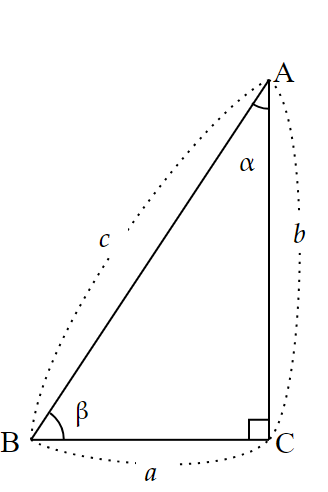
図1の$~\triangle ABC~$において、
\sin{A}=\frac{a}{c}~~,~~\cos{A}=\frac{b}{c}であるため、
\begin{align*}
\sin^2{A}+\cos^2{A}&=\frac{a^2}{c^2}+\frac{b^2}{c^2} \\
\\
&=\frac{a^2+b^2}{c^2}
\end{align*}
となる。
三平方の定理より、$~a^2+b^2=c^2~$なので、
\sin^2{A}+\cos^2{A}=\frac{c^2}{c^2}=1が求まる。$~~\blacksquare$

図2のような任意の三角形において、
a^2=b^2+c^2-2bc \cos{A}が成り立つ。
$~A~$が鋭角のときについてのみ示す。
$~C~$から$~AB~$に垂線 $~CH~$を下ろす。

このとき、三角比から
\begin{align*}
CH&=b\sin{A} \\
AH&=b\cos{A} \\
BH&=c-b \cos{A}
\end{align*}と表せる。
$~\triangle BCH~$で三平方の定理より、$~BC^2=CH^2+BH^2~$なので、
\begin{align*}
a^2&=(b\sin{A})^2+(c-b\cos{A})^2 \\
&=b^2\sin^2{A}+c^2-2bc\cos{A}+b^2\cos^2{A} \\
&=b^2(\sin^2{A}+\cos^2{A})+c^2-2bc\cos{A} \\
&=b^2+c^2-2bc\cos{A} \\
\end{align*}
が求まった。$~~\blacksquare$
証明2では、証明1の内容まで使っており、三角比の性質がいかに三平方の定理を基にしているかがわかります。
三角比を使った証明の誤った例
次に、三平方の定理の証明で勘違いが起こりやすいものを1つ紹介します。

図4で、
\sin{A}=\frac{a}{c}~~,~~\cos{A}=\frac{b}{c}であるため、
\begin{align*}
a^2+b^2&=c^2 \left( \frac{a^2}{c^2}+\frac{b^2}{c^2} \right) \\
\\
&=c^2(\sin^2{A}+\cos^2{A})
\end{align*}となる。
ここで、$~\sin^2{A}+\cos^2{A}=1~$より、
a^2+b^2=c^2 \cdot 1 =c^2
が求まる?
いかにも証明が達成されているように書いていますが、これは明らかな循環論法です。
循環論法というのは、結論を用いて証明をすること。
上記の証明で言えば、以下のように論理が循環しています。
- 三平方の定理を証明するために、$~\sin^2{A}+\cos^2{A}=1~$を利用する。
- $~\sin^2{A}+\cos^2{A}=1~$の証明には、三平方の定理を利用する。
このように、三平方の定理と三角比は密接にかかわっているため、長年三角比を利用した三平方の定理の証明は不可能とされてきました。
近年になって、循環論法を避けつつ三角比を利用した三平方の定理の証明方法が発案され始めたものの、難解で複雑なものが多いのが現状です。
そこに一石を投じたのが今回の証明でした。
三角比を使った証明方法
では、実際に三角比を用いた証明方法に入っていきます。
正弦定理の証明に三平方の定理は使わない
今回発見された方法では、余弦定理と並んでよく出てくる正弦定理を使用します。

図5のような任意の三角形$~ABC~$とその外接円の半径$~R~$について、
\frac{a}{\sin{A}}=\frac{b}{\sin{B}}=\frac{c}{\sin{C}}=2Rが成り立つ。
$~A~$が鋭角のときについてのみ示す。
外接円$~O~$に対し、$~B~$を通る直径を$~BD~$とすると、円周角の定理より、$~\angle A=\angle D~$。
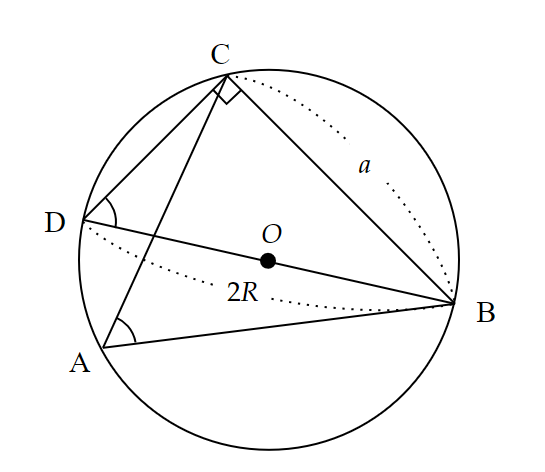
このとき、$~\triangle BCD~$で
\begin{align*}
\sin{D}&=\frac{a}{2R} \\
\\
\sin{A}&=\frac{a}{2R}\\
\\
2R&=\frac{a}{\sin{A}}
\end{align*}と表せる。
同様に、
2R=\frac{b}{\sin{B}}~~,~~2R=\frac{c}{\sin{C}}も表せるので、3つの式をまとめて、
\frac{a}{\sin{A}}=\frac{b}{\sin{B}}=\frac{c}{\sin{C}}=2Rが求まった。$~~\blacksquare$
余弦定理と違って、三平方の定理を証明に使っていないことがわかります。
三角比の定義と正弦定理を使って証明する
正弦定理を使う分には循環論法にならないことが確かめられたので、それを使って三平方の定理を証明します。
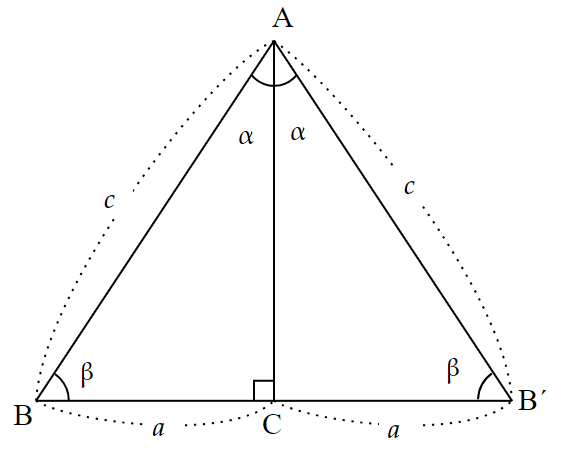
図5のような$~BC < AC~$である直角三角形$~ABC~$を考える。(一般性は失われない)
この$~\triangle ABC~$と相似な三角形を、次の手順で増やしていく。
(1) $~AC~$と線対称な$~\triangle AB^{\prime}C~$をつくる。
(2) $~BB^{\prime}~$よりも下側に、$~\triangle ABC~$∽$~\triangle BC^{\prime}B^{\prime}~$となる$~C^{\prime}~$をつくる。
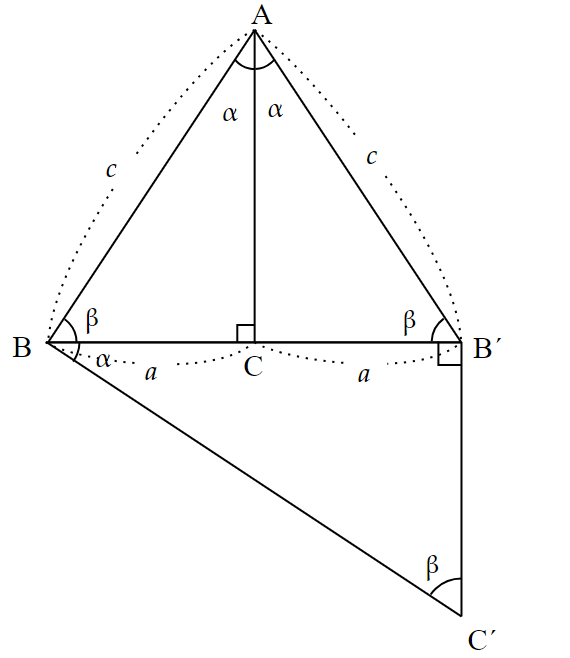
(3) $~B^{\prime}C^{\prime}~$よりも右側に、$~\triangle ABC~$∽$~\triangle B^{\prime}B^{\prime\prime}C^{\prime}~$となる$~B^{\prime\prime}~$をつくる。
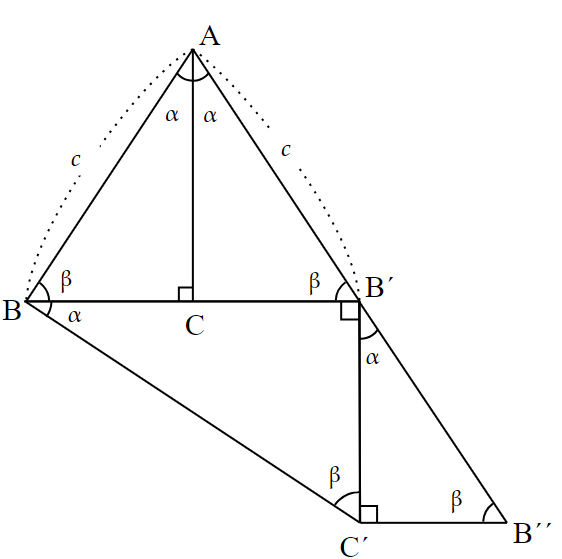
(4) (2)と(3)を繰り返していき、半直線$~AB^{\prime}~$と半直線$~BC^{\prime}~$の交点を$~D~$とする。
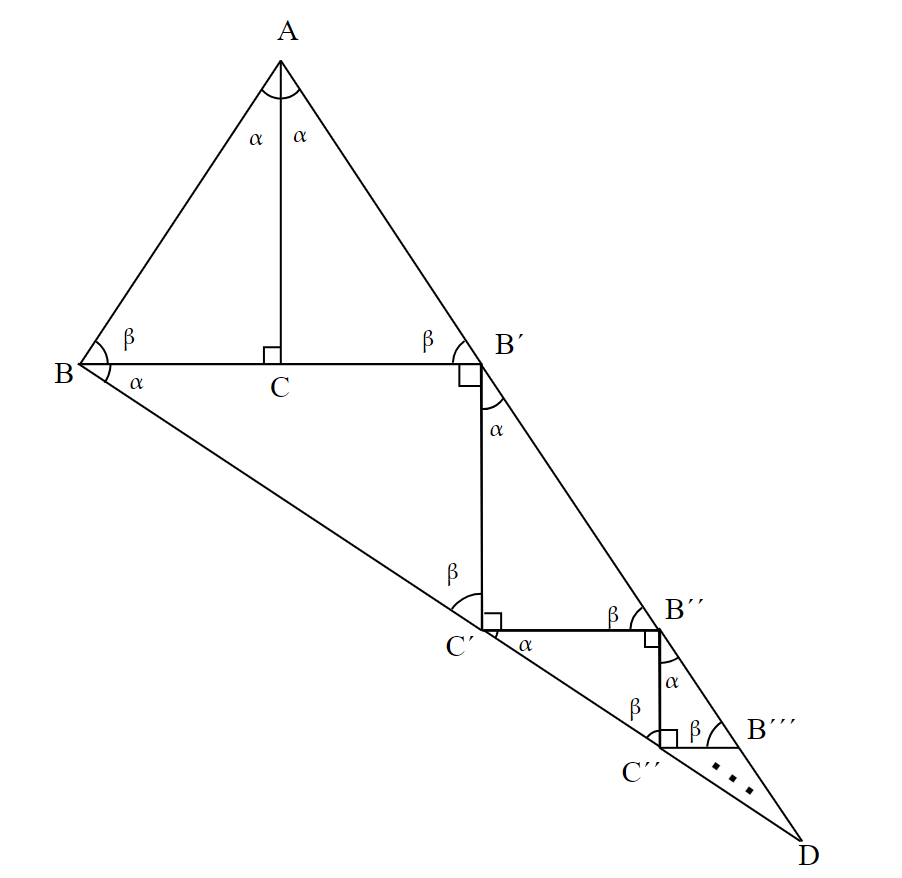
図9で登場する角度が$~90^{\circ}~,~\alpha~,~\beta~$の三角形について、$~\triangle ABC~$より、
\begin{align*}
\sin{\alpha}&=\cos{\beta}=\frac{a}{c} \\
\\
\sin{\beta}&=\cos{\alpha}=\frac{a}{c} \\
\end{align*}が成り立っている。
これにより、$~\triangle BC^{\prime}B^{\prime}~$の各辺の長さを求めると、$~BB^{\prime}=2a~$より、
\begin{align*}
\cos{\alpha}&=\frac{BB^{\prime}}{BC^{\prime}} \\
\\
\frac{b}{c}&=\frac{2a}{BC^{\prime}} \\
\\
BC^{\prime}&=\frac{2ac}{b}~~~\cdots①
\end{align*}と求まり、これにより、
\begin{align*}
\sin{\alpha}&=\frac{B^{\prime}C^{\prime}}{BC^{\prime}} \\
\\
\frac{a}{c}&=\frac{B^{\prime}C^{\prime}}{\frac{2ac}{b}} \\
\\
B^{\prime}C^{\prime}&=\frac{2a^2}{b}
\end{align*}となる。
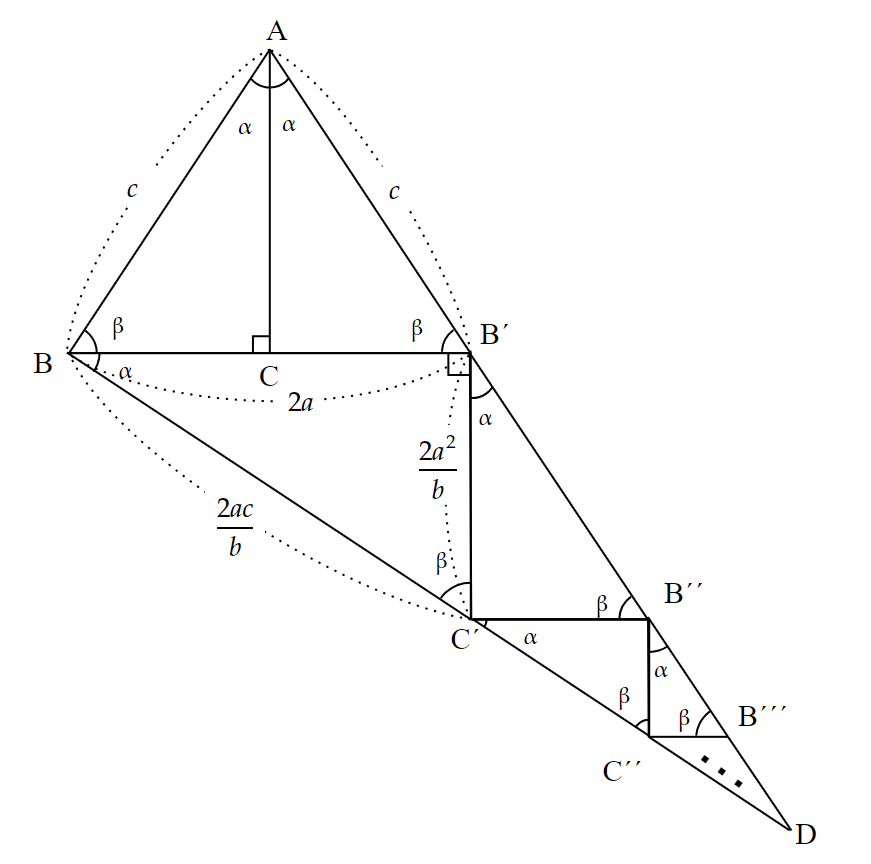
次に、$~\triangle B^{\prime}B^{\prime\prime}C^{\prime}~$の各辺の長さを求めると、
\begin{align*}
\cos{\alpha}&=\frac{B^{\prime}C^{\prime}}{B^{\prime}B^{\prime\prime}} \\
\\
\frac{b}{c}&=\frac{\frac{2a^2}{b}}{B^{\prime}B^{\prime\prime}} \\
\\
B^{\prime}B^{\prime\prime}&=\frac{2a^2c}{b}~~~\cdots②
\end{align*}と求まり、これにより、
\begin{align*}
\sin{\alpha}&=\frac{C^{\prime}B^{\prime\prime}}{B^{\prime}B^{\prime\prime}} \\
\\
\frac{a}{c}&=\frac{C^{\prime}B^{\prime\prime}}{\frac{2a^2c}{b^2}} \\
\\
C^{\prime}B^{\prime\prime}&=\frac{2a^3}{b^2}
\end{align*}となる。
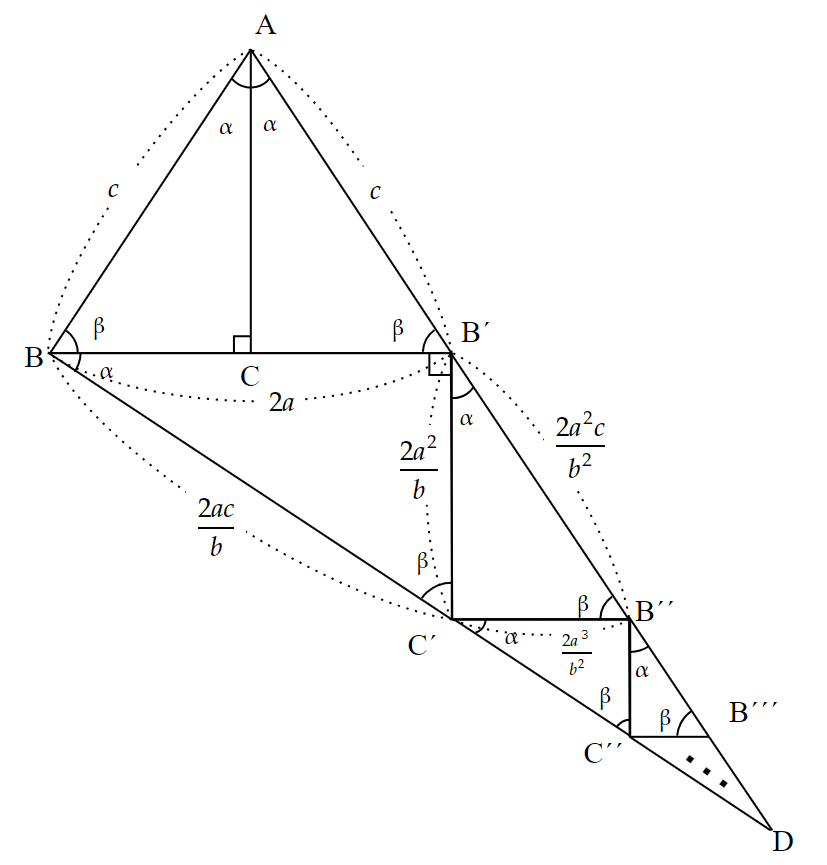
さらに、$~\triangle C^{\prime}C^{\prime\prime}B^{\prime\prime}~$の各辺の長さを求めると、
\begin{align*}
\cos{\alpha}&=\frac{C^{\prime}B^{\prime\prime}}{C^{\prime}C^{\prime\prime}} \\
\\
\frac{b}{c}&=\frac{\frac{2a^3}{b^2}}{C^{\prime}C^{\prime\prime}} \\
\\
C^{\prime}C^{\prime\prime}&=\frac{2a^3c}{b^3}~~~\cdots③
\end{align*}と求まり、これにより、
\begin{align*}
\sin{\alpha}&=\frac{B^{\prime\prime}C^{\prime\prime}}{C^{\prime}C^{\prime\prime}} \\
\\
\frac{a}{c}&=\frac{B^{\prime\prime}C^{\prime\prime}}{\frac{2a^3c}{b^3}} \\
\\
B^{\prime\prime}C^{\prime\prime}&=\frac{2a^4}{b^3}
\end{align*}となる。
したがって、$~\triangle B^{\prime\prime}B^{\prime\prime\prime}C^{\prime\prime}~$で、
\begin{align*}
\cos{\alpha}&=\frac{B^{\prime\prime}C^{\prime\prime}}{B^{\prime\prime}B^{\prime\prime\prime}} \\
\\
\frac{b}{c}&=\frac{\frac{2a^4}{b^3}}{B^{\prime\prime}B^{\prime\prime\prime}} \\
\\
B^{\prime\prime}B^{\prime\prime\prime}&=\frac{2a^4c}{b^4}~~~\cdots④
\end{align*}が求まる。
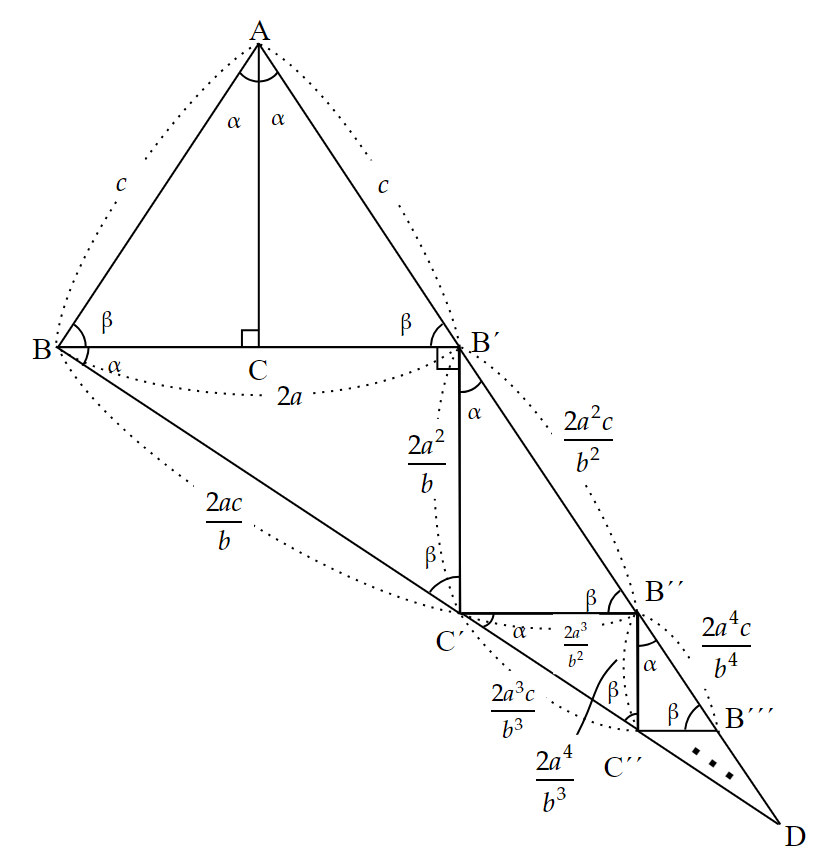
ここで、全体の三角形$~ABD~$を考えると、
\sin{2\alpha}=\frac{BD}{AD}~~~\cdots⑤である。
$~\triangle ABB^{\prime}~$で正弦定理を使うと、
\begin{align*}
\frac{c}{\sin{\beta}}&=\frac{2a}{\sin{2\alpha}} \\
\\
\frac{c}{\frac{b}{c}}&=\frac{2a}{\sin{2\alpha}} \\
\\
\sin{2\alpha}&=\frac{2ab}{c^2}~~~\cdots⑥
\end{align*}と求まる。
また、$~BD~$の長さは、$①$と$③$から初項$~\displaystyle \frac{2ac}{b}~$、公比$~\displaystyle \frac{a^2}{b^2}~$の無限等比級数の和なので、$~a < b~$より$~\displaystyle \frac{a^2}{b^2} < 1 ~$であることに注意して、
\begin{align*}
BD&=\frac{\frac{2ac}{b}}{1-\frac{a^2}{b^2}} \\
\\
&=\frac{2ac}{b-\frac{a^2}{b}} \\
\\
&=\frac{2abc}{b^2-a^2}~~~\cdots ⑦
\end{align*}と求まる。
同様に、$~AD~$の長さは、$~AB^{\prime}=c~$と$②$と$④$より、
\begin{align*}
AD&=c+\underbrace{\frac{2a^2}{b^2}+\frac{2a^4}{b^4}c+\cdots~~~~~~~~~~~~~}_{初項~\frac{2a^2}{b^2}c~,~公比~\frac{a^2}{b^2}~の等比級数の和} \\
\\
&=c+\frac{\frac{2a^2}{b^2}c}{1-\frac{a^2}{b^2}} \\
\\
&=\frac{b^2c-a^2c}{b^2-a^2}+\frac{2a^2c}{b^2-a^2} \\
\\
&=\frac{b^2c+a^2c}{b^2-a^2} \\
\\
&=\frac{c(b^2+a^2)}{b^2-a^2}~~~\cdots⑧
\end{align*}と求まる。
$⑥$~$⑧$を$⑤$に代入して、
\begin{align*}
\frac{2ab}{c^2}&=\frac{\frac{2abc}{b^2-a^2}}{\frac{c(b^2+a^2)}{b^2-a^2}} \\
\\
\frac{2ab}{c^2}&=\frac{2ab}{(b^2+a^2)} \\
\\
\frac{1}{c^2}&=\frac{1}{b^2+a^2} \\
\\
a^2+b^2&=c^2
\end{align*}となるため、三平方の定理が示された。$~~\blacksquare$
ていねいに解説しましたが、証明のシナリオとしては4ステップです。
- 相似な直角三角形を組み合わせて大きな直角三角形を作る。
- 三角比の定義を使い、構成する直角三角形の各辺を求める。
- 無限等比級数の和から、大きな直角三角形の辺を求める。
- 正弦定理で、大きな直角三角形の角の三角比を表す。
このように単純な計算だけで証明できるため、三角比を使った正しい証明の中で「最も美しい証明」とアメリカの数学会から評されています。
発見者はアメリカの10代の少女2人
最後に、この証明の発見者について言及しておきます。
近年、数学者によって三角比を使った証明方法は考えられてきましたが、今回の「最も美しい証明」の発見者は10代の少女2人です。

その2人とは、カルシア・ジョンソン氏とネキヤ・ジャクソン氏であり、アメリカ数学会に対してプレゼンを行い、その功績が認められました。
また、彼女らがアメリカの数学会に少ないアフリカ系アメリカ人の女性ということも脚光を浴びている一つの要因です。

三角比だけど、無限を使うから数学Ⅲの知識が必要だね。



うん。無限を使う証明自体なら、20世紀にJohn ArioniがFaceBookで発信した方法もあるよ。
三平方の定理の内容や、三平方の定理の別証についてはこちらから↓↓


参考文献
- Gigazine(2023年4月11日アクセス)<https://gigazine.net/news/20230410-teenagers-pythagorean/>

コメント
コメント一覧 (5件)
複素数を用いた加法定理の証明はリンク先の動画がわかりやすいです!
加法定理は三平方の定理を用いなくても証明できます!リンク先の画像の図形を用いれば倍角の公式も同時に証明できるので確認ください.
もしくは加法定理は複素数の積と偏角の関係からも導出できます.
沖縄数学アカデミー様
ド・モアブルの定理、加法定理、倍角の公式、距離の公式あたりが絡んでくるかと思いますので、自分でももう少し考えてみようと思います。
この度は様々な情報提供ありがとうございました。
確かに彼女らの証明方法は感動しますよね!
彼女らの証明をヒントに無限級数を用いない方法でも証明することができます.本日は倍角の公式です.
証明のyoutube動画をリンクしておきます!
沖縄数学アカデミー様
コメントいただきありがとうございます。
動画を拝見いたしまして、面白さを感じると同時に、一つ気になった点がございました。
それは、tanの2倍角の公式の証明に、三平方の定理を使っているのでは?という疑問です。
循環論法になってしまう気がしたのですが、三平方の定理を使わずに2倍角の公式を証明はできるのでしょうか?
自分の知識不足だったら申し訳ありません。
ご教示いただければと思います。