三平方の定理について、「公式自体は知っているけど、なんで成り立つの？」という疑問や、「100種類以上の証明方法ってどんなものがあるの？」という興味を持ったことはありませんか？
三平方の定理の証明については、紀元前6世紀から、数学者のみならずあらゆる人たちが挑み、多種多用な証明方法が生み出されています。
この記事では、三平方の定理の証明方法の概要を10種類以上、対象学年別に紹介。
個別ページでは、それにまつわる歴史や具体的な証明方法をわかりやすく解説しています。
この記事を読んで、自分に合った証明方法を探してみてください！
- なぜ三平方の定理の証明がたくさん生まれるようになったのか
- 対象学年別・三平方の定理の証明方法一覧
三平方の定理とは？
三平方の定理の歴史
三平方の定理の歴史は、紀元前1800年頃のバビロニア（今のイラク南部）にさかのぼります。
バビロニアでは、今で言うピタゴラス数（$~a^2+b^2=c^2~$を満たす自然数の組$~(~a~,~b~,~c~)~$）に関する数表が存在していました。
三平方の定理は別名「ピタゴラスの定理」とも呼ばれますが、ピタゴラス（Pythagoras, B.C.569頃-B.C.500頃）は、バビロニアにおける三平方の定理から約1300年後の人物なので、ピタゴラスが発見したというのは誤りになります。
（出典：The original uploader was Galilea at German Wikipedia., Public domain, via Wikimedia Commons）
それどころか、タレス（Thales, B.C.625頃-B.C.547頃）の助言により、ピタゴラスは若き頃にバビロニアを旅し、三平方の定理を学んだと言われています。
ピタゴラスは三平方の定理をギリシャに持ち帰り、この定理がなぜ成り立つのか、すなわち証明を世界で初めて行いました。（→「ピタゴラスによる証明」を参照）
それゆえに、ピタゴラスの名が定理についています。
ピタゴラスの死から約200年後、三平方の定理の証明ブームを巻き起こした数学者が現れます。
その人こそ、『原論』でお馴染みのユークリッド（Euclid , B.C.330頃-B.C.275頃）です。
（出典：Photograph taken by Mark A. Wilson (Wilson44691, Department of Geology, The College of Wooster).[1], Public domain, via Wikimedia Commons）
![Photograph taken by Mark A. Wilson (Wilson44691, Department of Geology, The College of Wooster).[1]](https://commons.wikimedia.org/wiki/File:EuclidStatueOxford.jpg){kind=link}
彼は後の何千年もの間、多くの人々に読まれることになる著書『原論』の中で、三平方の定理を紹介し、ピタゴラスのとは違うオリジナルの証明を与えました。 （→「ユークリッドによる証明」を参照）
それゆえ、三平方の定理は時代や国境を越えて知られるようになり、多様な証明が今も生まれ続けています。
三平方の定理の内容
証明に入る前に、三平方の定理の内容について、確認をしておきます。
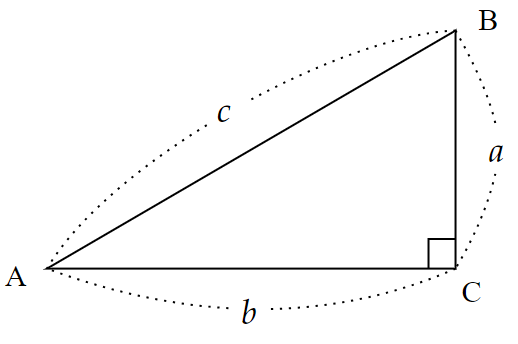
直角をはさむ辺の長さが$~a~,~b~$、斜辺が$~c~$である直角三角形において、
a^2+b^2=c^2
が成り立つ。
現在の学習指導要領では、中学校３年生の秋～冬にかけて学ぶ内容となっています。
しかし、証明の中にはパズルのように行うものもあり、文字式が使える中学校１年生、ひいては意味だけなら小学生以下でも理解することができます。
この記事では、理解できる学年ごとに区切って証明方法を紹介していきますが、文字式の意味を理解できるのが中１であることから、最低学年を中１と設定したうえで話を進めていきます。
中１レベルの証明
① ピタゴラスの証明
| 対象学年 | 複雑さ | 美しさ |
| 中学１年生 | ★☆☆☆☆ | ★★★☆☆ |
紀元前の数学者ピタゴラス（Pythagoras, B.C.569頃-B.C.500頃）が考えたもので、事実上三平方の定理初の証明方法です。
（出典：The original uploader was Galilea at German Wikipedia., Public domain, via Wikimedia Commons）
証明方法としては、下の図の黄色い長方形を切り分けて‥‥
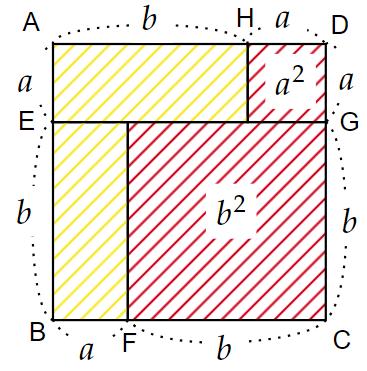
四隅に配置するだけ！
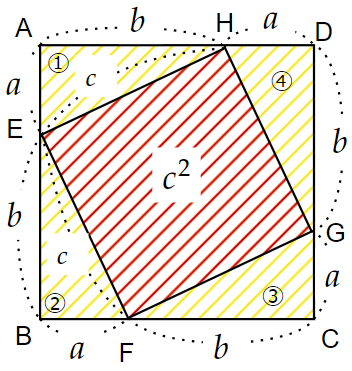
中２レベルの証明
② ユークリッドによる証明
| 対象学年 | 複雑さ | 美しさ |
| 中学２年生 | ★★★★★ | ★★★★☆ |
紀元前の数学者ユークリッド（Euclid , B.C.330頃-B.C.275頃）が考えたもので、ピタゴラスに次いで２番目に古い証明方法とされています。
（出典：Photograph taken by Mark A. Wilson (Wilson44691, Department of Geology, The College of Wooster).[1], Public domain, via Wikimedia Commons）
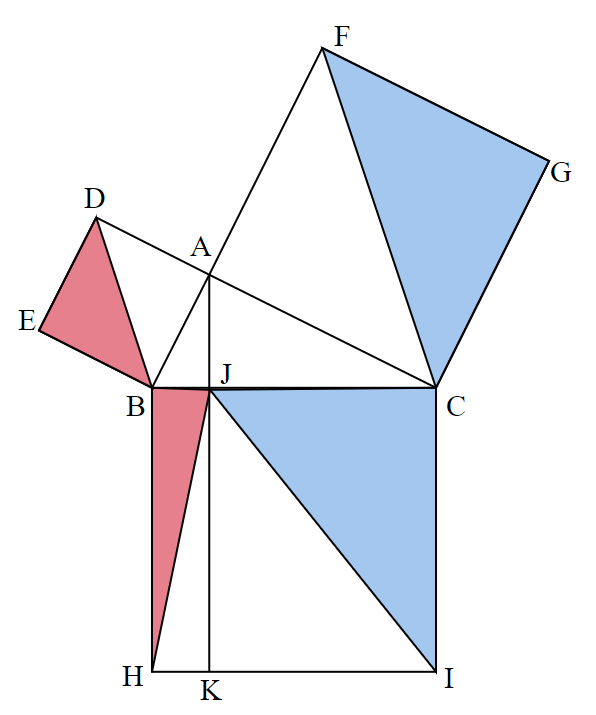
証明方法は、「花嫁の椅子」と呼ばれる図からスタートして、
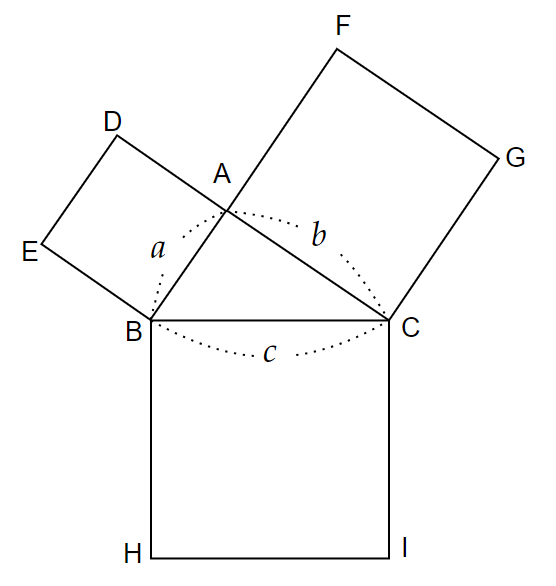
等積変形や合同を用いながら、$~\triangle DEB=\triangle HJB~$,$~\triangle FGC=\triangle IJC~$を示します。
⑥ レオナルド・ダ・ヴィンチによる証明
| 対象学年 | 複雑さ | 美しさ |
| 中学２年生 | ★★★★☆ | ★★★★★ |
「モナ・リザ」や「最後の晩餐」を書いたことで知られる芸術家 レオナルド・ダ・ヴィンチ（Leonardo da Vinci , 1452-1519） が考えた証明方法です。
（出典；Leonardo da Vinci, Public domain, via Wikimedia Commons）
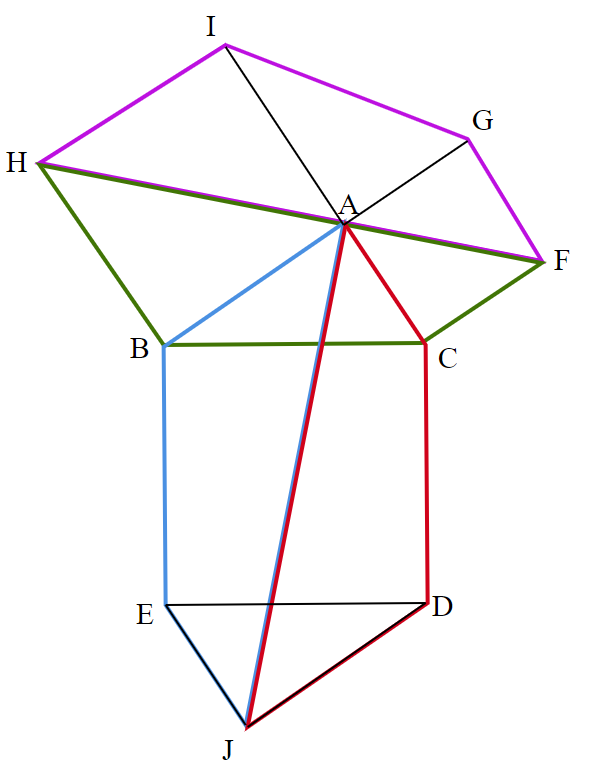
ユークリッドの「花嫁の椅子」に補助線を引き、合同な四角形を４つ作ることで証明を行います。
⑨ コンディット（アメリカの少女）による証明
| 対象学年 | 複雑さ | 美しさ |
| 中学２年生 | ★★★★★ | ★★★☆☆ |
1938年、当時16歳であったアメリカ合衆国の少女アン・コンディット（Ann Cindit , 1922-不明） が、補助線を巧みに利用して、三平方の定理を証明しました。
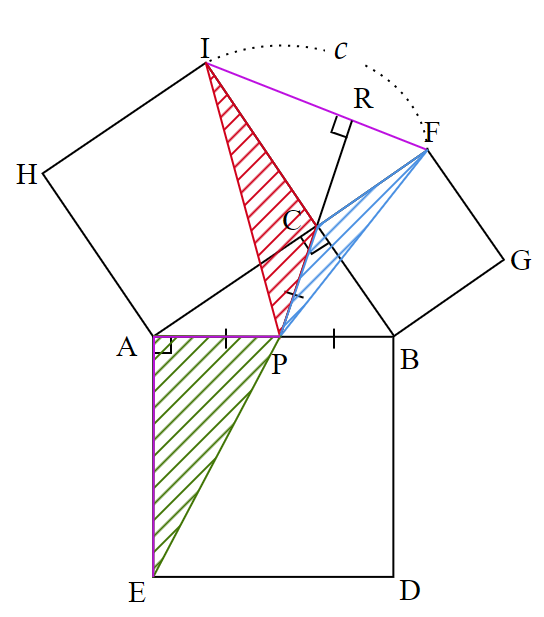
中３で理解できる証明方法
③内接円を利用した証明方法
| 対象学年 | 複雑さ | 美しさ |
| 中学３年生 | ★★★☆☆ | ★☆☆☆☆ |
1927年に出版された『ピタゴラスの命題』の著者であるイライシャ・スコット・ルーミス（Elisha Scott Loomis , 1582-1940）が発見したと主張している証明方法です。
（出典：Finkel, B. F., Public domain, via Wikimedia Commonsより改変）
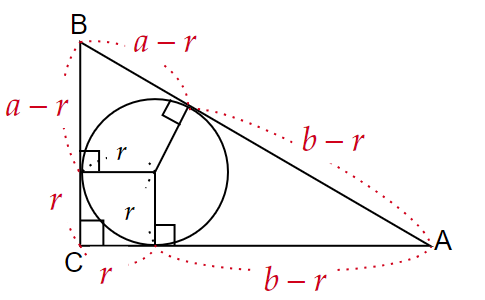
直角三角形の中に半径$~r~$の内接円を描き、面積や辺の長さの関係から$~r~$を消去することで、証明ができます。
⑧ ガーフィールド（アメリカの大統領）による証明
| 対象学年 | 複雑さ | 美しさ |
| 中学３年生 | ★★☆☆☆ | ★★★☆☆ |
アメリカ合衆国の政治家ジェームズ・A・ガーフィールド（James Abram Garfield , 1831-1881）が、大統領になる前に思いついたとされる証明方法です。
（出典：Unknown; part of Brady-Handy Photograph Collection., Public domain, via Wikimedia Commons）
直角三角形を２つ組み合わせることで台形を作り、面積を２通りの方法で表すことで証明します。
⑪ アインシュタインによる証明
| 対象学年 | 複雑さ | 美しさ |
| 中学３年生 | ★★☆☆☆ | ★★☆☆☆ |
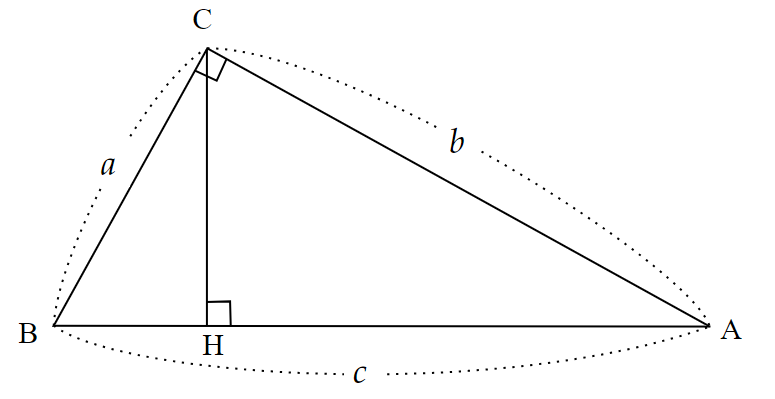
相対性理論で有名な物理学者 アルベルト・アインシュタイン（Albert Einstein , 1879-1955） が、16歳のときに発見した証明方法です。
（出典：Ferdinand Schmutzer, Public domain, via Wikimedia Commons）
補助線１本を引くことで現れる３つの相似な三角形（ $~\triangle ABC~$∽$~\triangle CBH~$ ）の面積比を利用する方法です。
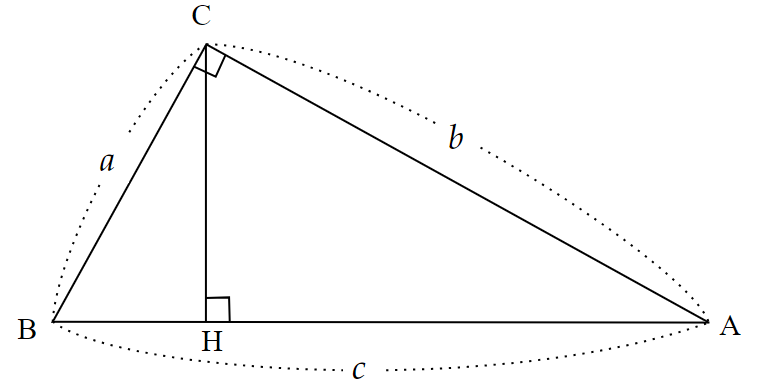
⑫ 相似を利用した最も簡単な証明
| 対象学年 | 複雑さ | 美しさ |
| 中学３年生 | ★☆☆☆☆ | ★★☆☆☆ |
アインシュタインの方法と同様の図で、こちらは面積比ではなく線分比から三平方の定理を導く方法です。
多くの書物に掲載されている、三平方の定理の代表的な証明方法の１つとなっています。
⑭ 教科書に最もよく登場する証明
| 対象学年 | 複雑さ | 美しさ |
| 中学３年生 | ★☆☆☆☆ | ★☆☆☆☆ |
直角三角形４つを組み合わせて正方形を作り、面積を２通りの方法で表すことで三平方の定理が導けます。
ほとんどの教科書で採用されている証明方法です。
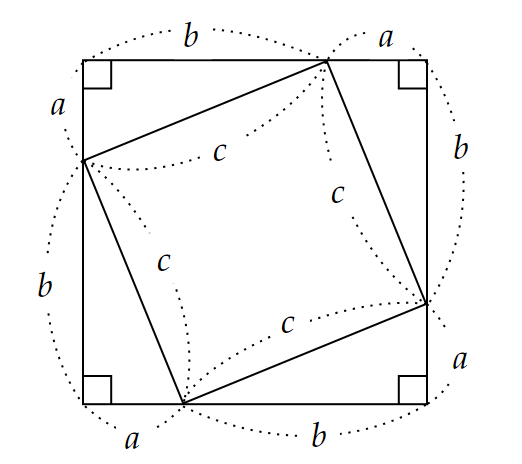
⑮ バスカラの証明
| 対象学年 | 複雑さ | 美しさ |
| 中学３年生 | ★☆☆☆☆ | ★☆☆☆☆ |
中世インドの大数学者バスカラ（Bhaskara , 1114-1185頃）が、算術について記した書『リーラ―ヴァ―ティー』 の中で、図で示した証明方法です。
直角三角形４つを組み合わせて正方形を作り、面積を２通りの方法で表すことで三平方の定理が導けます。
「 ⑭教科書に最もよく登場する証明 」とは、組み合わせ方が異なるだけです。
高１（数学Ⅰ・A）で理解できる証明方法
④ 方べきの定理を利用した証明１
| 対象学年 | 複雑さ | 美しさ |
| 高校１年生（数学A） | ★☆☆☆☆ | ★★☆☆☆ |
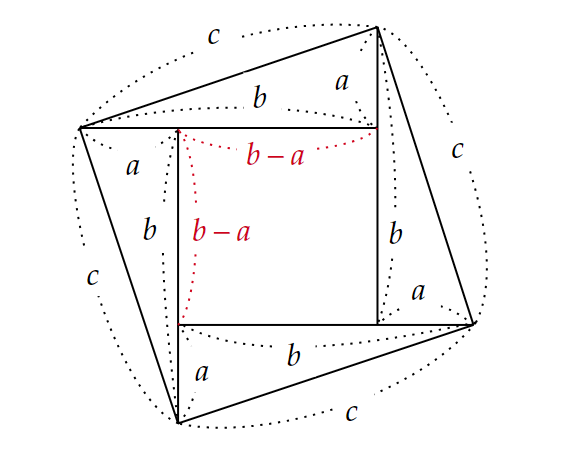
３種類の方べきの定理のうち、円の内部で２つの直線が交わっているパターンを利用した証明方法です。
⑤ 方べきの定理を利用した証明２
| 対象学年 | 複雑さ | 美しさ |
| 高校１年生（数学A） | ★☆☆☆☆ | ★★☆☆☆ |
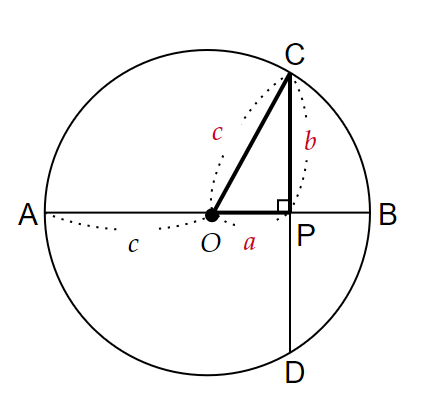
３種類の方べきの定理のうち、円の外部で２つの直線が交わり、そのうち１つが接線のタイプを利用した証明方法です。
⑦ トレミーの定理を利用した証明
| 対象学年 | 複雑さ | 美しさ |
| 高校１年生（数学A） | ★☆☆☆☆ | ★★☆☆☆ |
トレミーとは、 ローマ時代の数学者クラウディオス・プトレマイオス （Claudius Ptolemaeus , 85頃-165頃） のことで、天文学を研究する中で、円に内接する四角形に関する「トレミーの定理」を発見しました。
（出典：Unknown authorUnknown author, Public domain, via Wikimedia Commons）
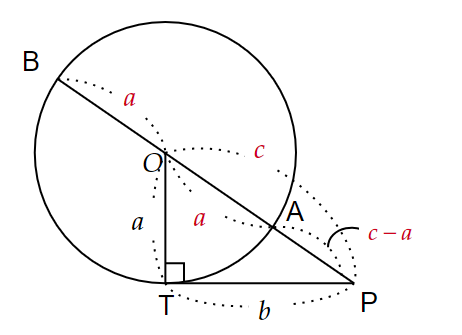
三平方の定理を証明するためには、長方形を円に内接させ、トレミーの定理を使うだけ。
ただ、トレミーの定理の証明が大変です。
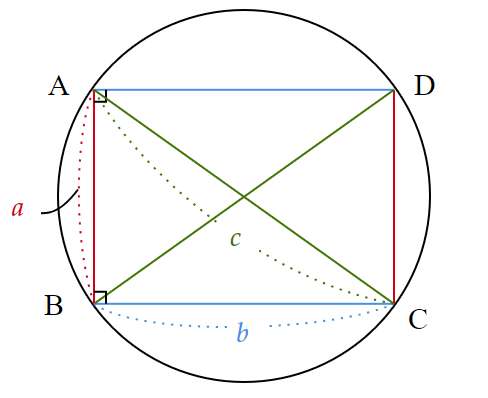
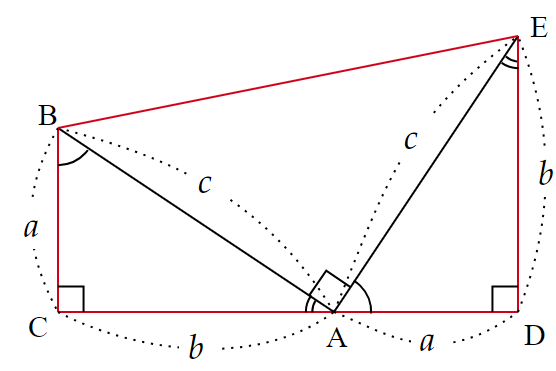
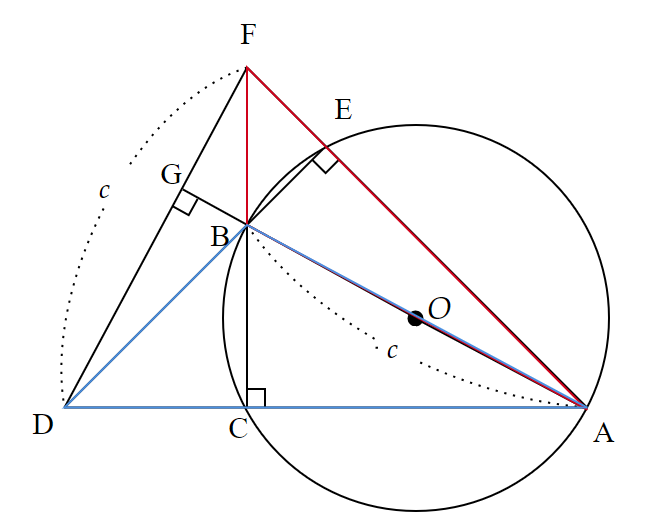
⑬ 外接円と直角二等辺三角形を利用した証明
| 対象学年 | 複雑さ | 美しさ |
| 高校１年生（数学A） | ★★★★★ | ★★★★☆ |
SNSで数学の面白さを発信しているベトナム人の Bui Quang Tuan（1962～）によって考案された証明方法です。
直角二等辺三角形２つと外接円を追加することで、合同な三角形や垂心が誕生し、それらの性質をうまく使って証明します。
高３（数学Ⅲ）で理解できる証明方法
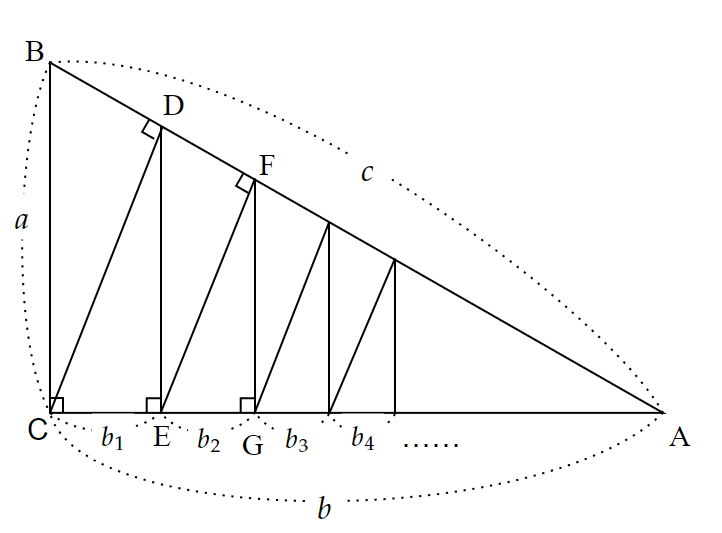
⑩ 無限等比級数による証明
| 対象学年 | 複雑さ | 美しさ |
| 高校３年生（数学Ⅲ） | ★★★★★ | ★★★★☆ |
Facebookで数学関連のことを発信している John Arioni（1948～）が発案した証明方法です。
直角から垂線を下ろし、その直角からまた垂線を下ろし‥‥、ということを無限に繰り返していくことで、三平方の定理が現れます。
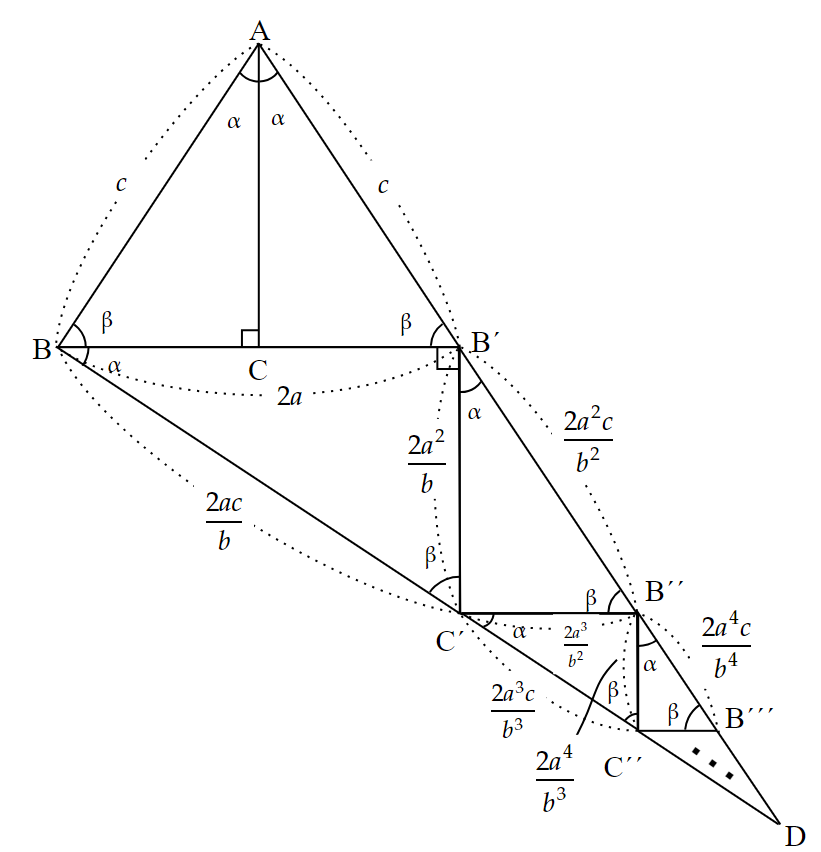
⑯ 三角比と無限等比級数による証明
| 対象学年 | 複雑さ | 美しさ |
| 高校３年生（数学Ⅲ） | ★★★★★ | ★★★★★ |
2023年4月、アメリカの少女2人が学会で発表した証明です。
循環論法になりやすいとされる三角比を使い、見事に無限等比級数に帰着させて証明しています。
コメント
コメント一覧 （6件）
結構わかりやすくて読みやすかったです
証明のまとめ見たいなと思っていたので助かりました
まとめてくださりありがとうございます
嬉しいコメントありがとうございます！
今後も面白そうな証明を見つけ次第、更新していく予定です。
是非またいらしてください。
わかりにくいのもあったしわかるものもあった
コメントありがとうございます。
わかりやすいものだけでも、学びに繋がっていたら幸いです。
わかりやすい
コメントありがとうございます！
励みになります！！
今後ともよろしくお願いします。