Σシグマの公式一覧〜教科書には出てこない4乗や5乗の求め方も3通り解説！

2025年9月26日2025年10月13日

当ページのリンクには広告が含まれています。

　数列の和を求めるのに使うシグマ記号$~\sum~$。

　高校の教科書では0乗（定数）和から3乗和までを学びますが、実は4乗や5乗、それ以上についても公式があります！

\sum_{k=1}^{n}k^{4}=\frac{1}{30}n(n+1)(2n+1)(3n^2+3n-1)

　本記事では、シグマ$~\sum~$の和の公式の一覧から、各指数における求め方や歴史までを数学史の先生Fukusukeがわかりやすく解説。

　この記事を読むことで、なぜ高校数学で学ぶのは3乗までなのかも見えてくることでしょう。

この記事を書いた人

Fukusuke（ふくすけ）
数学史の先生

現役の中学・高校数学教員
著書2冊重刷、ブログ累計200万PV達成
行間がなくなるほど丁寧な式変形で執筆中

この記事を書いた人

Fukusuke（ふくすけ）
数学史の先生

現役の中学・高校数学教員
著書2冊は発売1ヶ月で即重刷
当数学史ブログは累計200万PV達成
行間がなくなるほど丁寧な式変形で記事を執筆

『世界を変えた数学史図鑑』『教養としての数学史』好評発売中！

この記事を読んでわかること

シグマ公式一覧

　まずは、シグマの公式を10乗和まで一覧にしました。

$~\sum_{k=1}^{n}k^{10}~$までの公式

\begin{align*} \displaystyle \sum_{k=1}^{n}k^{0}&=n ~~~~~~~~~~~~~~~~~\left( \sum_{k=1}^{n}1=n \right)\\ \\ \displaystyle \sum_{k=1}^{n}k^{1}&=\frac{1}{2}n(n+1) \\ \\ \displaystyle \sum_{k=1}^{n}k^{2}&=\frac{1}{6}n(n+1)(2n+1) \\ \\ \displaystyle \sum_{k=1}^{n}k^{3}&=\frac{1}{4}n^2(n+1)^2 \\ \\ \displaystyle \sum_{k=1}^{n}k^{4}&=\frac{1}{30}n(n+1)(2n+1)(3n^2+3n-1) \\ \\ \displaystyle \sum_{k=1}^{n}k^{5}&=\frac{1}{12}n^2(n+1)^2(2n^2+2n-1) \\ \\ \displaystyle \sum_{k=1}^{n}k^{6}&=\frac{1}{42}n(n+1)(2n+1)(3n^4+6n^3-3n+1) \\ \\ \displaystyle \sum_{k=1}^{n}k^{7}&=\frac{1}{24}n^2(n+1)^2(3n^4+6n^3-n^2-4n+2) \\ \\ \displaystyle \sum_{k=1}^{n}k^{8}&=\frac{1}{90}n(n+1)(2n+1)(5n^6+15n^5+5n^4-15n^3-n^2+9n-3) \\ \\ \displaystyle \sum_{k=1}^{n}k^{9}&=\frac{1}{20}n^2(n+1)^2(n^2+n-1)(2n^4+4n^3-n^2-3n+3) \\ \\ \displaystyle \sum_{k=1}^{n}k^{10}&=\frac{1}{66}n(n+1)(2n+1)(n^2+n-1) (3n^6+9n^5+2n^4-11n^3+3n^2+10n-5) \\ \end{align*}

　$~n~$や$~(n+1)~$が共通していることは見えてきますが、係数を含めたそれ以外の部分については規則性が見えてきません。

　実は現在のところ、各公式を瞬時に表すような公式は見つかっておらず、特に4乗和以降についてはそれ未満の次数の公式を利用して証明することになります。

3乗和まで限定のシグマ公式の求め方

　自然数の0乗和$~\displaystyle \sum_{k=1}^{n}1~$、1乗和$~\displaystyle \sum_{k=1}^{n}k~$、2乗和$~\displaystyle \sum_{k=1}^{n}k^2~$、3乗和$~\displaystyle \sum_{k=1}^{n}k^3~$の4つの公式については、それぞれ限定の求め方があります。

0乗和と1乗和は数列の公式で求められる

　最初の2つについては、非常に簡単。
　中学受験にも登場する等差数列の和の公式を利用します。

0乗和と1乗和の公式の求め方

　$~\sum~$の記号の意味から考えると、$~\displaystyle \sum_{k=1}^{n}1~,~\displaystyle \sum_{k=1}^{n}k~$はそれぞれ以下のように変形できる。

\begin{align*} \sum_{k=1}^{n}1&=\underbrace{1+1+\cdots+1}_{1がn個} \\ &=1\times n \\ &=n \ \ \end{align*}

\begin{align*} \sum_{k=1}^{n}k&=\underbrace{1+2+3+\cdots+n}_{初項1,末項n,項数nの等差数列} \\ &=\frac{1}{2}n(n+1) \end{align*}

　以上より、0乗和と1乗和のシグマ公式が求められた。$~~~\blacksquare~$

　1乗和の公式については、初項$~1~$、公差$~1~$、項数$~n~$の等差数列であることから、以下のようにも当然求められます。

\begin{align*} \sum_{k=1}^{n}k&=1+2+3+\cdots+n\\ &=\frac{1}{2}n\{2\cdot 1+(n-1)\cdot 1\} \\ &=\frac{1}{2}n(n+1) \\ \end{align*}

2乗和は図形的に求められる

　$~\displaystyle \sum_{k=1}^{n}k^2~$については、後述する「4乗和以上も求められる教科書的方法」で求めるのが一般的ですが、実は次のような美しい求め方もあります。

2乗和の公式の求め方

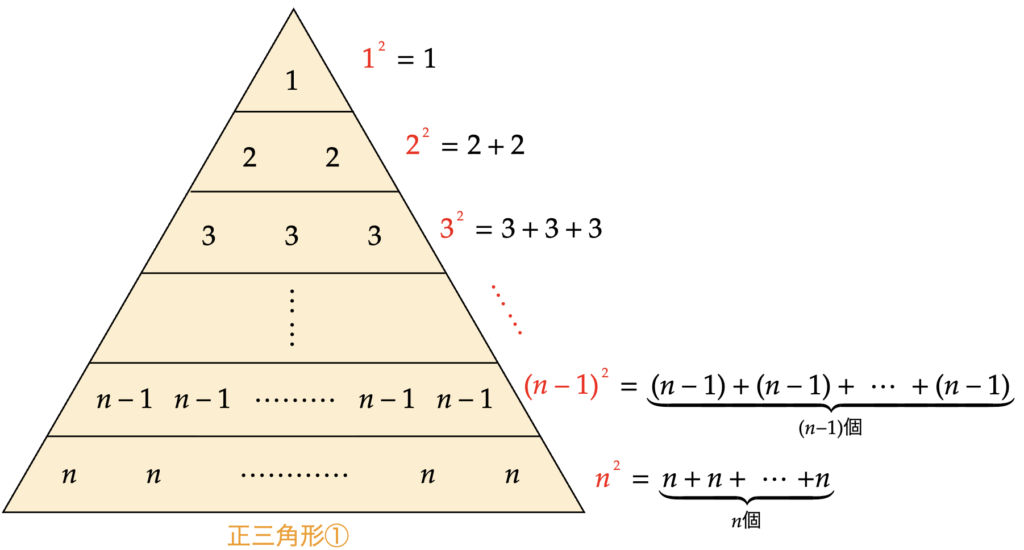
\begin{align*} &~~~~\sum_{k=1}^{n}k^2 \\ &=1^2+2^2+3^2+\cdots+(n-1)^2+n^2 \\ &=\underbrace{1\times1}_{1が1個}+\underbrace{2\times2}_{2が2個}+\underbrace{3\times3}_{3が3個}+\cdots+\underbrace{(n-1)\times(n-1)}_{(n-1)が(n-1)個}+\underbrace{n\times n}_{nがn個} \\ &=1+(2+2)+(3+3+3)+\cdots \\ &~~~~~~~+\left\{(n-1)+(n-1)+\cdots+(n-1)\right\}+ (n+n+\cdots+n) \\ \end{align*}

と変形し、これらの各項を次のような正三角形状に並べる。

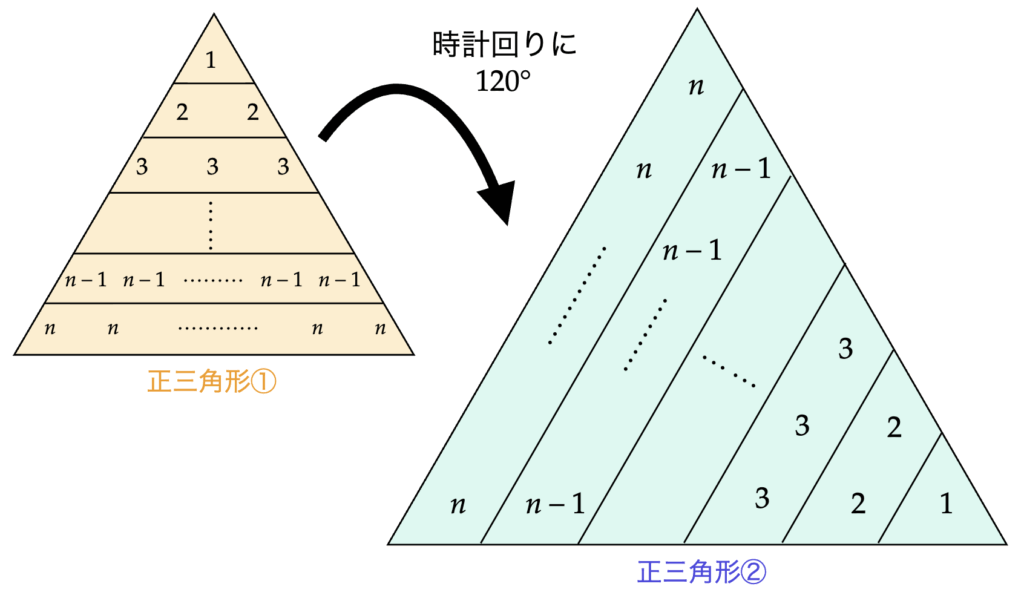
　さらに、この正三角形①を時計回りに$~120^{\circ}~$回転させた正三角形②と、反時計回りに$~120^{\circ}~$回転させた正三角形③を作る。

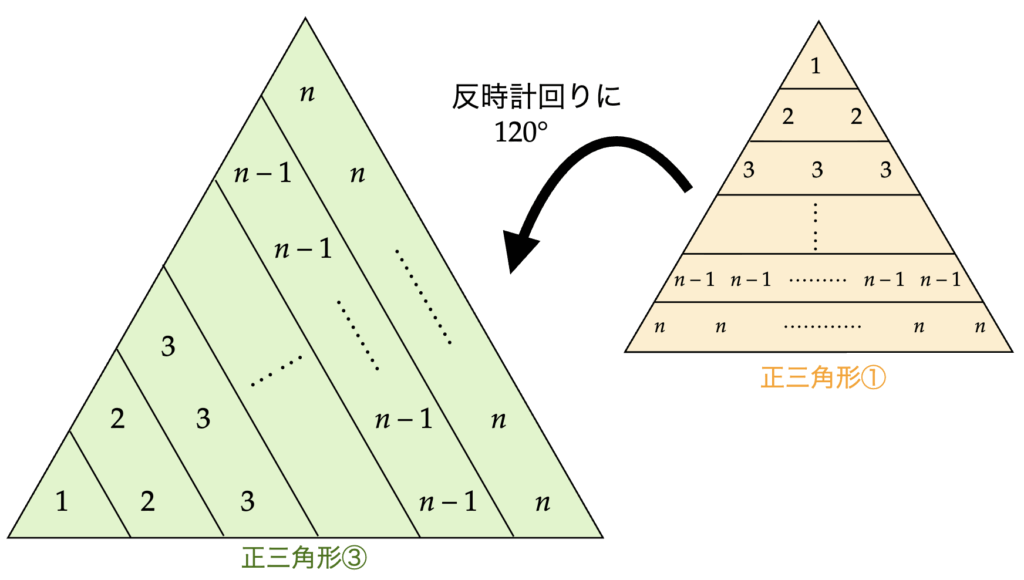
　正三角形①〜③を重ねて、同じ場所にある3つの数をすべて足してできる正三角形は次のようになる。

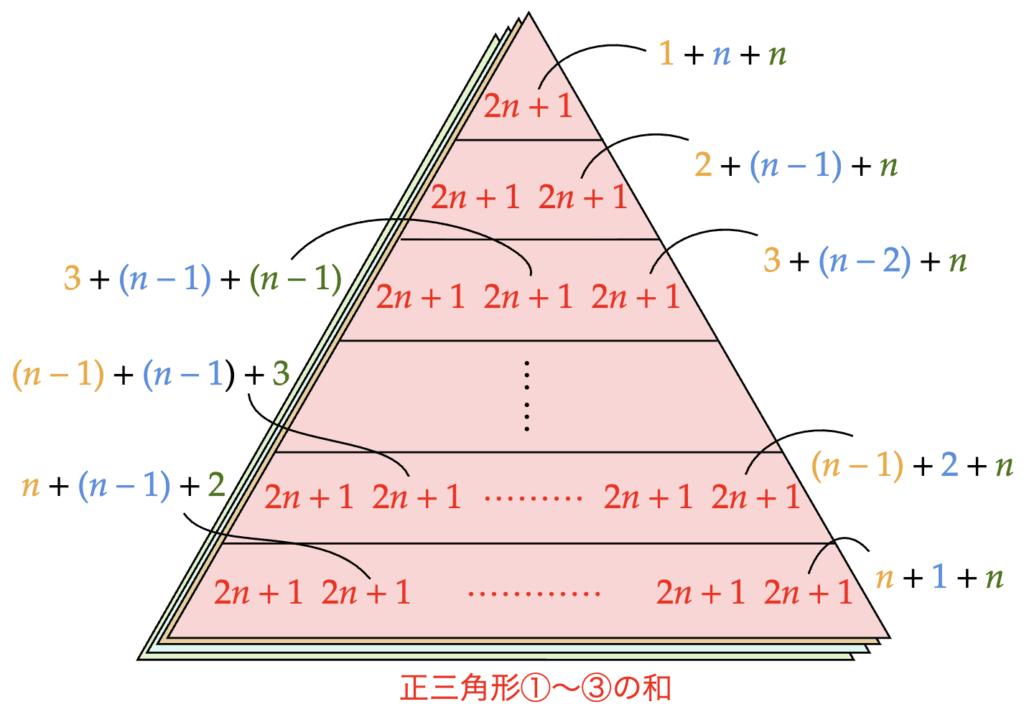
　この正三角形に登場する数の個数は、

1+2+3+\cdots+(n-1)+n=\frac{1}{2}n(n+1)~ ~~~個

であり、数の合計は、

\frac{1}{2}n(n+1)\times (2n+1)=\frac{1}{2}n(n+1)(2n+1)

である。正三角形①の数の合計は$~\displaystyle \sum_{k=1}^{n}k^2~$であり、正三角形②と正三角形③も同様だったので、以上のことから、以下の等式が成り立つ。

3\sum_{k=1}^{n}k^2 =\frac{1}{2}n(n+1)(2n+1)

すなわち、

\sum_{k=1}^{n}k^2 =\frac{1}{6}n(n+1)(2n+1)

という2乗和のシグマ公式が求められた。$~~~\blacksquare~$

　2乗和だったので、平面三角形を利用して求められました。
　次の3乗和は二コマコスが立方体を利用して求めていますが、4乗和以降に適用できる方法ではありません。

3乗和は二コマコスの定理で求められる

　数学Bで暗記が求められるのは3乗和の公式まで。
　3乗和の公式も、後述する「4乗和以上も求められる教科書的方法」で求めるのが一般的ですが、次の定理を利用するという方法があります。

ニコマコスの定理

　$~n~$を自然数とする。
　$~1~$から$n$までの整数の立方和は、1からnまでの整数和の平方に等しい。

1^3 + 2^3 + 3^3 + \cdots + n^3 = (1 + 2 + 3 + \cdots + n)^2

　この定理は、ローマ帝国で活躍した数学者ニコマコス（Nicomachus , 60年頃〜120年頃）が、100年ごろに書いた『算術入門』の中で述べたものです。

二コマコス
（出典：AnonymousUnknown author, Public domain, via Wikimedia Commons）

二コマコスの定理を使うことで、1乗和の公式から3乗和の公式を導けます。

3乗和の公式の求め方

　二コマコスの定理と1乗和の公式により、$~\displaystyle \sum_{k=1}^{n}k^3~$は次のように変形できる。

\begin{align*} \sum_{k=1}^{n}k^3&=1^3 + 2^3 + 3^3 + \cdots + n^3 \\ &= (\underbrace{1 + 2 + 3 + \cdots + n}_{1乗和})^2 \\ &=\left\{\frac{1}{2}n(n+1) \right\}^2 \\ &=\frac{1}{4}n^2(n+1)^2 \end{align*}

　以上より、3乗和のシグマ公式が求められた。$~~~\blacksquare~$

　二コマコスは以下のような図を利用して説明したため、どんな$~n~$でも成り立つかまでは保証していません。

　ただ、二コマコス自身が発見した立方数の性質と、ピタゴラス（Pythagoras , B.C.569頃～B.C.500頃）が発見した奇数の和の公式を組み合わせることにより、どんな$~n~$でも二コマコスの定理が成り立つことは言及できたと考えられます。

4乗和以降のシグマ公式の求め方

　これまでに解説した方法は、特定の累乗和のみで使えるもので4乗和以降には適用できません。
　しかし、これから紹介する3つの求め方は、4乗和以降でも使えて時間さえかければどんな累乗和でも求められる方法です。

　求め方の比較も兼ねて、4乗和の公式を3つの方法で求めてみましょう。

4乗和の公式

\displaystyle \sum_{k=1}^{n}k^4=\frac{1}{30}n(n+1)(2n+1)(3n^2+3n-1)

教科書に載っている求め方

　数学Bの教科書に載っている方法です。
　3乗和までの公式を知っていれば、以下のような方法で4乗和の公式を求めることができます。

4乗和のシグマ公式の求め方（教科書的）

(k+1)^5-k^5 =5k^4+10k^3+10k^2+5k+1

を考える。

　両辺$~k=1~$から$~k=n~$までの和、すなわち$~\displaystyle \sum_{k=1}^{n}~$ をとると、

\displaystyle \sum_{k=1}^{n} \{(k+1)^5-k^5 \}=\sum_{k=1}^{n} (5k^4+10k^3+10k^2+5k+1 ) \text{・・・①}

となる。

　まず、左辺を式変形していくと、

\begin{align*} &（左辺）\\ &=(2^5-1^5)+(3^5-2^5)+(4^5-3^5)+\cdots+\{(n+1)^5-n^5\} \\ &=(n+1)^5-1 \\ &=(n^5+5n^4+10n^3+10n^2+5n+1)-1 \\ &=n^5+5n^4+10n^3+10n^2+5n \end{align*}

　同様に、右辺を式変形していくと、

\begin{align*} &（右辺）\\ &=\displaystyle 5\sum_{k=1}^{n}k^4+10\sum_{k=1}^{n}k^3+10\sum_{k=1}^{n}k^2+5\sum_{k=1}^{n}k+\sum_{k=1}^{n}1 \\ \\ &=5\sum_{k=1}^{n}k^4+10\cdot\left\{ \frac{1}{2}n(n+1) \right\}^2+10\cdot\frac{1}{6}n(n+1)(2n+1)+5\cdot\frac{1}{2}n(n+1)+n \\ \\ &=5\sum_{k=1}^{n}k^4+\frac{5}{2}n^2(n+1)^2 +\frac{5}{3}n(n+1)(2n+1)+\frac{5}{2}n(n+1)+n \\ \\ &=5\sum_{k=1}^{n}k^4+\frac{5}{2}n^2(n^2+2n+1) +\frac{5}{3}n(2n^2+3n+1)+\frac{5}{2}n(n+1)+n \\ \\ &=5\sum_{k=1}^{n}k^4+\frac{5}{2}n^4+5n^3+\frac{5}{2}n^2+\frac{10}{3}n^3+5n^2+\frac{5}{3}n+\frac{5}{2}n^2+\frac{5}{2}n+n \\ \\ &=5\sum_{k=1}^{n}k^4+\frac{5}{2}n^4+\frac{25}{3}n^3+10n^2+\frac{31}{6}n \\ \end{align*}

　よって、$①$は、

\displaystyle n^5+5n^4+10n^3+10n^2+5n=5\sum_{k=1}^{n}k^4+\frac{5}{2}n^4+\frac{25}{3}n^3+10n^2+\frac{31}{6}n

となり、式変形をしていくと、

\begin{align*} \displaystyle \sum_{k=1}^{n}k^4&=\frac{1}{5}\left( n^5+\frac{5}{2}n^4+\frac{5}{3}n^3-\frac{1}{6}n \right)\\ \\ &=\frac{1}{30}n ( \underbrace{6n^4+15n^3+10n^2-1}_{n=1のとき0になる}) \\ \\ &=\frac{1}{30}n(n+1) ( \underbrace{6n^3 + 9n^2 + n - 1}_{n=-\frac{1}{2}のとき0になる}) \\ \\ &=\frac{1}{30}n(n+1)(2n+1)( 3n^2+3n-1) \\ \end{align*}

となり、4乗和のシグマ公式が求められた。$~\blacksquare~$

　同様に、$~\displaystyle \sum_{k=1}^{n}k^5~$なら、$~(k+1)^6-k^6~$ を、$~\displaystyle \sum_{k=1}^{n}k^6~$なら、$~(k+1)^7-k^7~$ を、考えることで求められます。

　また、$~(k+1)-k~$を考えれば$~\displaystyle \sum_{k=1}^{n}1~$が求められるように、低次数の場合についても求めることができるのが特徴です。

\begin{align*} (k+1)-k&=1 \\ (n+1)-1&=\sum_{k=1}^{n}1 \\ n&=\sum_{k=1}^{n}1 \\ \end{align*}

アルハゼンの公式による求め方

　中世イスラームの数学者アルハゼン（Alhazen、965〜1040）は、次のような公式を発見しました。

アルハゼンの和の公式

(n+1)\sum_{i=1}^{n} i^k = \sum_{i=1}^{n} i^{k+1} + \sum_{p=1}^{n} \left(\sum_{i=1}^{p} i^k\right)

　3乗和までの公式を知っていれば、アルハゼンの和の公式により、4乗和の公式が求められます。

4乗和のシグマ公式の求め方（アルハゼン）

　アルハゼンの和の公式に$~k=3~$を代入すると、

\begin{align*} (n+1)\sum_{i=1}^{n}i^3&= \sum_{i=1}^{n}i^4 + \sum_{p=1}^{n}\left(\sum_{i=1}^{p}i^3\right)\\ (n+1)\left\{\frac{1}{2}n(n+1)\right\}^2&= \sum_{i=1}^{n}i^4 + \sum_{p=1}^{n}\left\{\frac{1}{2}p(p+1)\right\}^2 \\ \frac{1}{4}n^2(n+1)^3&= \sum_{i=1}^{n}i^4 + \sum_{p=1}^{n}\left\{\frac{1}{4}p^2(p+1)^2\right\} \cdots ② \end{align*}

となり、最終項を変形すると、

\begin{align*} \sum_{p=1}^{n}\left\{\frac{1}{4}p^2(p+1)^2\right\} &= \frac{1}{4}\sum_{p=1}^{n}p^2(p^2+2p+1) \\ &= \frac{1}{4}\sum_{p=1}^{n}(p^4+2p^3+p^2) \\ &= \frac{1}{4}\sum_{p=1}^{n}p^4 + \frac{2}{4}\left\{\frac{1}{2}n(n+1)\right\}^2 + \frac{1}{4} \cdot \frac{1}{6}n(n+1)(2n+1) \\ &= \frac{1}{4}\sum_{p=1}^{n}p^4 + \frac{1}{8}n^2(n+1)^2 + \frac{1}{24}n(n+1)(2n+1) \cdots ③ \end{align*}

となるため、$~\sum_{p=1}^{n}p^4 = \sum_{i=1}^{n}i^4~$であることに注意し、③を②に代入すると、

\begin{align*} \frac{1}{4}n^2(n+1)^3 &= \sum_{i=1}^{n}i^4 + \frac{1}{4}\sum_{i=1}^{n}i^4 + \frac{1}{8}n^2(n+1)^2 + \frac{1}{24}n(n+1)(2n+1) \\ \frac{1}{4}n^2(n+1)^3 &= \frac{5}{4}\sum_{i=1}^{n}i^4 + \frac{1}{8}n^2(n+1)^2 + \frac{1}{24}n(n+1)(2n+1) \\ \frac{5}{4}\sum_{i=1}^{n}i^4 &= \frac{1}{4}n^2(n+1)^3 - \frac{1}{8}n^2(n+1)^2 - \frac{1}{24}n(n+1)(2n+1) \\ \sum_{i=1}^{n}i^4 &= \frac{4}{5} \cdot \frac{1}{24}n(n+1)\{6n(n+1) - 3n(n+1) - (2n+1)\} \\ \sum_{i=1}^{n}i^4 &= \frac{1}{30}n(n+1)(6n^2+12n^2+6n-3n^2-3n-2n-1) \\ \sum_{i=1}^{n}i^4 &= \frac{1}{30}n(n+1)(\underbrace{6n^3 + 9n^2 + n - 1}_{n=-\frac{1}{2}のとき0になる}) \\ \sum_{i=1}^{n}i^4 &= \frac{1}{30}n(n+1)(2n+1)(3n^2+3n-1) \end{align*}

となり、4乗和のシグマ公式が求められた。$~\blacksquare~$

　注意点として、$~k=0~$をアルハゼンの和の公式に代入して求められるのは、$~\displaystyle \sum_{k=1}^{n}k~$です。

　$~\displaystyle \sum_{k=1}^{n}1=n~$だけは、これまでに紹介した別の方法を利用する必要があります。

ファウルハーバーの公式による求め方

　17世紀のドイツの数学者ヨハン・ファウルハーバー（Johann Faulhaber ,1580 〜1635）の名が冠されている公式です。

ファウルハーバーの公式

　ベルヌーイ数$~B_n~$を次のように定義する。（Cは組み合わせ）

B_0 = 1, \quad \sum_{i=0}^{k}\left\{ (-1)^i \cdot~ _{k+1}\mathrm{C}_{i}~\cdot~B_i \right\}= 0 \quad~~~~ (k = 1,2,\cdots)

　このとき、次の等式をファウルハーバーの公式という。

\sum_{i=1}^{n} i^k= \frac{1}{k+1}\sum_{i=0}^{k} \left( ~_{k+1} \mathrm{C}_{i} \cdot B_i~\cdot n^{k+1-i} \right) \quad (k = 0,1,\cdots)

　ベルヌーイ数は日本の関孝和（1637〜1708）やスイスのヤコブ・ベルヌーイ（Jakob Bernoulli , 1654〜1705）が発見したものであり、このベルヌーイ数をもってファウルハーバーの公式が完成されました。

　ベルヌーイ数の定義の仕方はいくつかあるものの、上記のように定義した場合は次のようにベルヌーイ数が求められます。

B_1=\frac{1}{2}~,~B_2=\frac{1}{6}~,B_3=0~,~B_4=-\frac{1}{30}~

　これらの値をファウルハーバーの公式に代入して、4乗和の公式を求めてみましょう。

4乗和のシグマ公式の求め方（ファウルハーバー）

　ファウルハーバーの公式に、$~k = 4~$を代入すると、

\sum_{i=1}^{n}i^4 = \frac{1}{5}\sum_{i=0}^{4}\left( _{5}\mathrm{C}_i \cdot B_i \cdot n^{5-i}\right) ~~~\cdots ④

である。

ここで、右辺の$\sum$の中身を$~i = 0~,~1~,~2~,~3~,~4~$について、それぞれ計算すると、

\begin{align*} _5\mathrm{C}_0 \cdot B_0 \cdot n^5 &= 1 \cdot 1 \cdot n^5 = n^5 \\ _5\mathrm{C}_1 \cdot B_1 \cdot n^4 &= 5 \cdot \frac{1}{2} \cdot n^4 = \frac{5}{2}n^4 \\ _5\mathrm{C}_2 \cdot B_2 \cdot n^3 &= 10 \cdot \frac{1}{6} \cdot n^3 = \frac{5}{3}n^3 \\ _5\mathrm{C}_3 \cdot B_3 \cdot n^2 &= 10 \cdot 0 \cdot n^2 = 0 \\ _5\mathrm{C}_4 \cdot B_4 \cdot n^1 &= 5 \cdot \left(-\frac{1}{30}\right) \cdot n = -\frac{1}{6}n \end{align*}

なので、これらを④に代入することで、

\begin{align*} \sum_{i=1}^{n}i^4 &= \frac{1}{5}\left(n^5 + \frac{5}{2}n^4 + \frac{5}{3}n^3 + 0 - \frac{1}{6}n\right) \\ &= \frac{1}{30}n(\underbrace{6n^4+15n^3+10n^2-1}_{n=1のとき0になる}) \\ &= \frac{1}{30}n(n+1)(\underbrace{6n^3 + 9n^2 + n - 1}_{n=-\frac{1}{2}のとき0になる}) \\ &= \frac{1}{30}n(n+1)(2n+1)(3n^2 + 3n - 1) \end{align*}

となり、4乗和のシグマ公式が求められた。$~~~\blacksquare~$

　ファウルハーバーの公式では、3乗和以下の公式を使わずに4乗和の公式を求めているように思えますが、ベルヌーイ数$~B_4~$を求めるときに$~B_0~,~B_1~,~B_2~,~B_3~$を使っているため、これまでの公式と同様、いきなり4乗和や5乗和を求めることは不可能です。

　ただ、アルハゼンの和の公式と違って、ファウルハーバーの公式であれば0乗和の公式も求めることができます。

\begin{align*} \sum_{i=1}^{n}i^0 &= \frac{1}{1}\sum_{i=0}^{0}\left( _{1}\mathrm{C}_i \cdot B_i \cdot n^{1-i}\right) \\ &=1\cdot B_0\cdot n \\ &=n \end{align*}

まとめ

　この記事では、和の記号$~\sum~$（シグマ）による累乗和の公式について解説してきました。

3乗和までの公式と4乗和以降の公式の発見では、約900年の隔たりがある。
3乗和の公式までは図形的にも証明可能。
4乗和以降の公式を求めるためには3通りの方法があり、どれもそれより低次元の公式を得ている必要がある。

結局、なんで高校数学では3乗和までしか覚えないの？

我々の住んでいる空間が3次元であること、3乗和と4乗和で時代的な隔たりがあることなどが挙げられるけど、一番は4乗和以降は公式が複雑であることだろうね。同じ理由で、方程式の解の公式も3次は複雑過ぎて覚えないから。