
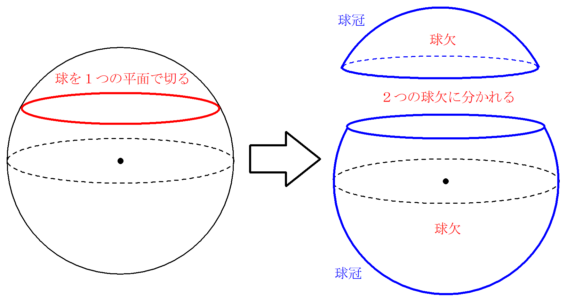
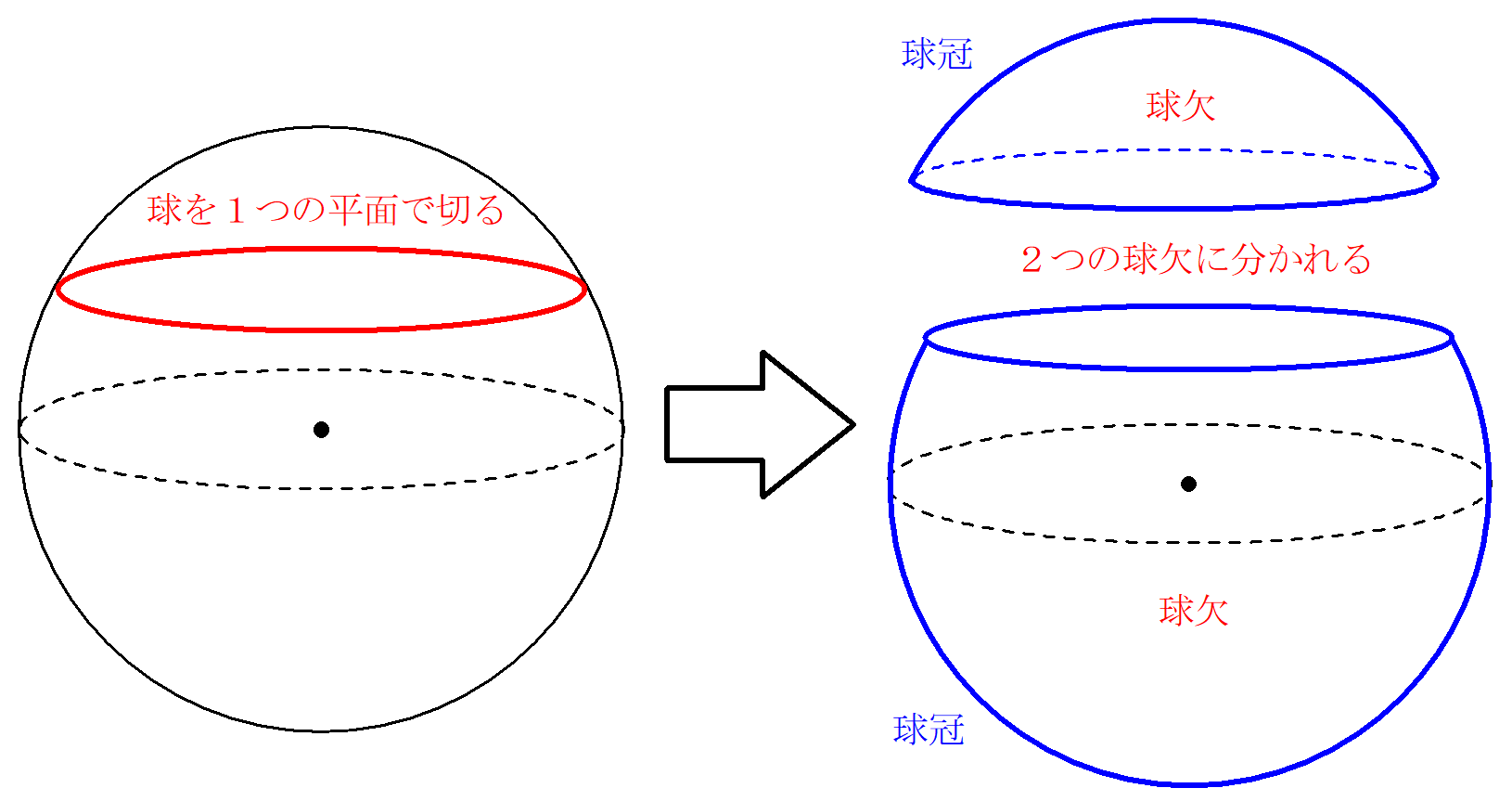
球を1つの平面で切り取ってできる球欠という立体について解説します。
知っていれば凸レンズの体積や表面積が求められるようになる!?
- 「球欠」と「球冠」の言葉の意味
- 球欠の体積の求め方
- 球冠の面積の求め方
Ⅰ 球欠と球冠の定義
言葉としてはあまり聞いたことのない「球欠」と「球冠」。
まずは言葉の意味を確認しておきます。
- 球を1つの平面で切り取ったときにできる立体のことを球欠という。
- 球欠の側面部分(もとの球面部分)のことを球冠という。

言葉の意味を考えてみると、
- 球が欠けている。
- 図1の2つの球欠のうち、下の球欠をひっくり返すと王冠のようになる。(王冠で装飾が施されるのは表面だけ)
あたりが由来かと思います。

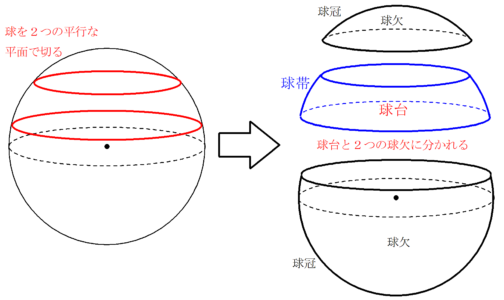
ちなみに、球を2つの平行な平面で切ると、「球台」となります。
Ⅱ 球欠の体積
球欠はもとの球の半径とは関係なく、体積が求まります。
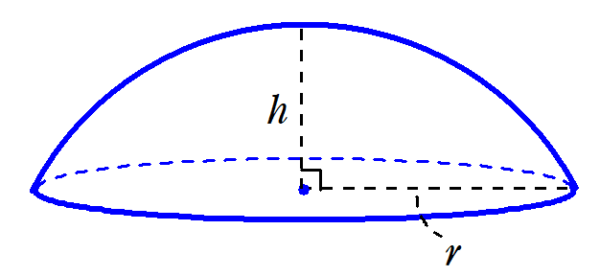

図3のような、切り口の円の半径が$~r~$、切り口の円の中心から球冠までの距離が$~h~$である球欠の体積は、
\begin{equation*}
\frac{\pi h}{6}(h^2+3r^2)
\end{equation*}と表せる。
意外とシンプルな式ですね。
半球を例に挙げて、この公式があてはまっているかを確認してみましょう。
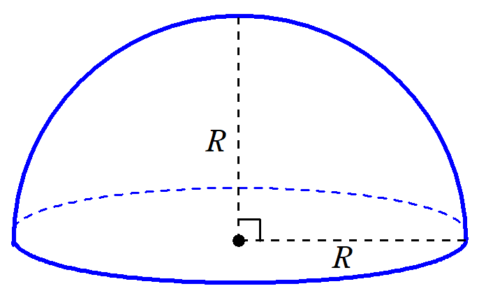

この半球は、切り口の円の半径$~r=R~$、切り口の円の中心から球冠までの距離$~h=R~$の球欠とみなすことができるので、
\begin{align*}
&~~~\frac{\pi h}{6}(h^2+3r^2) \\
\\
&=\frac{\pi R}{6}(R^2+3R^2) \\
\\
&=\frac{\pi R}{6}\cdot 4R^2 \\
\\
&=\frac{2}{3}\pi R^3 \\
\end{align*}と体積が求まる。
球の体積の公式を使えば、半球の体積は
\begin{equation*}
\frac{1}{2}\cdot \frac{4}{3}\pi R^3=\frac{2}{3} \pi R^3
\end{equation*}となるので、確かに球欠の公式で求めた結果と一致しています。
では、球欠の体積の公式を証明してみましょう。
もとの球の半径を$~R~$とし、図5のような座標空間上で考える。
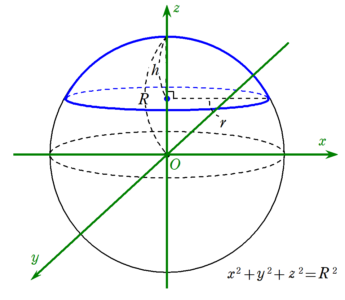

この図において、もとの球の方程式は
\begin{equation*}
x^2+y^2+z^2=R^2
\end{equation*}であり、平面$~z~~(-R < z < R )~$でもとの球を切ったとき、切り口の円の方程式は、
\begin{equation*}
x^2+y^2=R^2-z^2
\end{equation*}であるため、切り口の円の半径は$~\sqrt{R^2-z^2}~$である。
したがって、平面$~z~$における切り口の円の面積は
\begin{equation*}
\pi (\sqrt{R^2-z^2})^2=\pi (R^2-z^2)
\end{equation*}となる。
求めたい球欠の体積は、平面$~z~$における切り口の円を、$~z=R-h~$から$~z=R~$まで積分したものとなるため、
\begin{align*}
&~~~\int_{R-h}^{R}\pi(R^2-z^2)~dz \\
\\
&=\pi \int_{R-h}^{R}R^2-z^2~dz \\
\\
&=\pi \left[ R^2z-\frac{1}{3}z^3 \right]_{R-h}^{R} \\
\\
&=\pi \left\{ R^3-\frac{1}{3}R^3-R^2(R-h)+\frac{1}{3}(R-h)^3 \right\} \\
\\
&=\pi \left\{ \frac{2}{3}R^3-R^3+R^2h+\frac{1}{3}(R^3-3R^2h+3Rh^2-h^3) \right\} \\
\\
&=\pi \left( -\frac{1}{3}R^3+R^2h+\frac{1}{3}R^3-R^2h+Rh^2-\frac{1}{3}h^3 \right) \\
\\
&=\pi \left( Rh^2-\frac{1}{3}h^3 \right) ~~~~\cdots ①
\end{align*}とわかる。
ここで、図6の三角形に注目する。
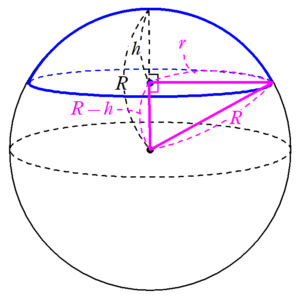

三平方の定理より、
\begin{align*}
R^2&=(R-h)^2+r^2 \\
R^2&=R^2-2Rh+h^2+r^2 \\
2Rh&=h^2+r^2 \\
R&=\frac{h^2+r^2}{2h}~~~~\cdots ②\\
\end{align*}と表せるため、球欠の体積は、$~②~$を$~①~$に代入することで、
\begin{align*}
&=\pi \left( \frac{h^2+r^2}{2h}\cdot h^2-\frac{1}{3}h^3 \right) \\
\\
&=\pi \left( \frac{h^2+r^2}{2}\cdot h-\frac{1}{3}h^3 \right) \\
\\
&=\pi \left( \frac{h^3+hr^2}{2}-\frac{1}{3}h^3 \right) \\
\\
&=\frac{\pi}{6}(3h^3+3hr^2-2h^3) \\
\\
&=\frac{\pi}{6}(h^3+3hr^2) \\
\\
&=\frac{\pi h}{6}(h^2+3r^2)
\end{align*}が求まった。■
$①$の式は、もとの球の半径$~R~$と、切り口の円の中心から球冠までの距離$~h~$だけで表せているため、球欠の体積を求めるためには、
- $~R~$と$~h~$
- $~r~$と$~h~$
のどちらかがわかっていれば良いということになります。
Ⅲ 球冠の面積
次に球冠の面積ですが、球欠と同様に もとの球の半径とは関係なく、面積が求まります。


図7のような、切り口の円の半径が$~r~$、切り口の円の中心から球冠までの距離が$~h~$である球冠の面積は、
\begin{equation*}
\pi (h^2+r^2)
\end{equation*}と表せる。
球欠の体積よりもさらにシンプルな式です。
こちらについても、まずは半球を使って確認してみましょう。


この半球は、切り口の円の半径$~r=R~$、切り口の円の中心から球冠までの距離$~h=R~$の球欠とみなすことができるので、
\begin{align*}
\pi (h^2+r^2)&=\pi(R^2+R^2) \\
&=2\pi R^2
\end{align*}と面積が求まる。
球の表面積の公式を使えば、半球の側面積(もとの球面の部分)は、
\begin{equation*}
\frac{1}{2}\cdot 4\pi R^2=2 \pi R^2
\end{equation*}となるので、確かに球冠の面積の公式で求めた結果と一致しています。
球冠の面積の公式についても証明してみましょう。
もとの球の半径を$~R~$として、次のアイスクリーム型の立体(以下「アイス体」)を考える。
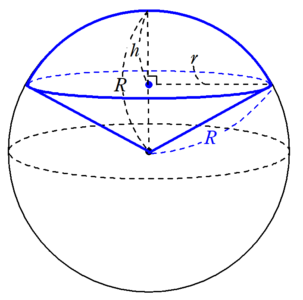

このアイス体は、球欠と円錐からできている。
$①$より、アイス体の球欠の体積は$~R~$と$~h~$を使って、
\pi \left( Rh^2-\frac{1}{3}h^3 \right)~~~\cdots ③と表せ、アイス体の円錐の体積は、底面の半径が$~r~$、高さが$~R-h~$なので、
\frac{1}{3}\pi r^2(R-h)~~~~\cdots ④と表せる。
$③$と$④$より、アイス体の体積は、
\begin{align*}
&~~~\pi \left( Rh^2-\frac{1}{3}h^3 \right)+\frac{1}{3}\pi r^2(R-h) \\
\\
&=\frac{\pi}{3} \left\{ 3Rh^2-h^3+r^2(R-h) \right\}
\end{align*}であり、$②$を変形することで得られる$~r^2=2Rh-h^2~$を代入すると、
\begin{align*}
&=\frac{\pi}{3} \left\{ 3Rh^2-h^3+(2Rh-h^2)(R-h) \right\} \\
\\
&=\frac{\pi}{3} \left( 3Rh^2-h^3+2R^2h-2Rh^2-Rh^2+h^3 \right) \\
\\
&=\frac{\pi}{3} \cdot 2R^2h \\
\\
&=\frac{2}{3} \pi R^2h
\end{align*}とアイス体の体積が求まった。
このアイス体は、球冠の面積$~S~$を使って、$~\displaystyle \frac{1}{3}SR~$とも表せるため、
\begin{align*}
\frac{1}{3}SR&=\frac{2}{3} \pi R^2h \\
\\
S&=2\pi Rh
\end{align*}と求まる。
ここで、$②$を代入すると、
\begin{align*}
S&=2\pi \cdot \frac{h^2+r^2}{2h} \cdot h \\
\\
&=\pi(h^2+r^2)
\end{align*}と求めたい式に変形された。■
※マーカー部の「球冠の面積$~S~$を使って、$~\displaystyle \frac{1}{3}SR~$とも表せる」について、補足。
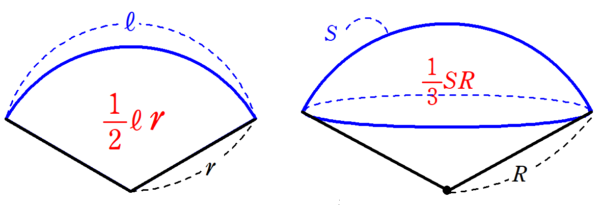

扇形の面積が、
\frac{1}{2} \times(弧の長さ)\times(半径)という公式で、三角形と同じように求めることができるのと同様、アイス体の体積は、
\frac{1}{3} \times(球冠の面積)\times(半径)という公式で、錐体と同じように求めることができます。
また、この証明の中で登場する、球冠の面積$~S=2\pi Rh~$という式ですが、
球冠の面積は、もとの球から切断するときの厚さ$~h~$に比例する
ということを意味しています。
こういう観点からでも美しいですね。



球を切った立体に名前がついていることに驚きΣ(゚Д゚)



しかも球欠の側面にまで、球冠という名前がついているからね。
コメント
コメント一覧 (2件)
球欠の体積の公式が二つあるんですけど、後者の方は球冠の面積では?
誤りなのであれば返事ください。
通りすがりの〇才さん
該当箇所を、球冠の面積に書き換えました。
ご指摘いただけて嬉しいです。
ありがとうございました。