球を2つの平面で切り取ってできた球台について考えます。
Ⅰ 球台と球帯とは?
Ⅱ 球台の体積
Ⅲ 球帯の面積
Ⅰ 球台と球帯とは?
前記事の「球欠と球冠」同様、聞き慣れない言葉である「球台」と「球帯」。まずはそれらの定義をお示しします。
球を2つの平行な平面で切り取ったときにできる立体のことを球台という。
球台の側面部分(もとの球面部分)のことを球帯という。
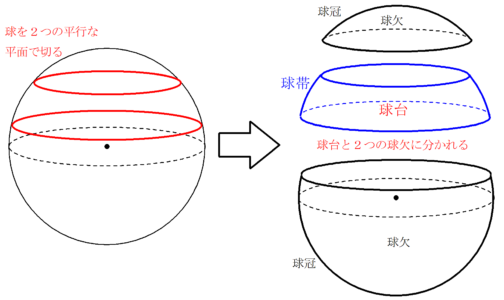
これまた球欠と球冠同様、ごもっともな名前が付いていることがわかります。
・円錐を底面と平行な平面で切り取ったときの立体を「円錐台」(下の図のプリン型)と言うため、その球バージョンなので「球台」。
・球を切り取ってできた帯(ベルト)のようなものだから「球帯」
(球台の側面部分だけなので、輪のようになる)
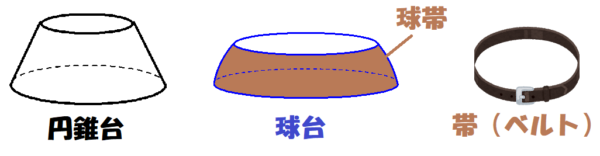
この記事では、球台の体積と球帯の面積について考えていきます。
Ⅱ 球台の体積
「球欠の体積」よりは複雑になりますが、割とシンプルな式で表すことができます。
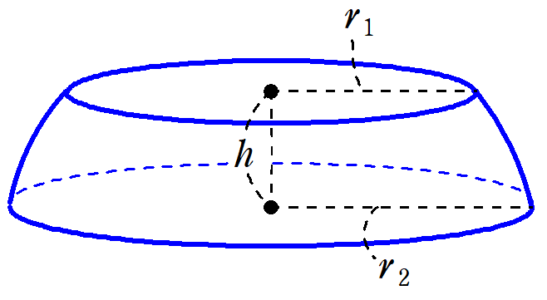
上図のような、天面の円の半径が$~r_1~$、底面の円の半径が$~r_2~$、天面と底面の距離が$~h~$である球台の体積は、
\begin{equation}
\frac{\pi h}{6}(h^2+3r_1^2+3r_2^2)
\end{equation}
と表せる。
非常に球欠の体積の公式と似ていますね。
この式さえ覚えておけば、天面の円の半径を$~r_1=0~$とすることで、球欠の体積の公式
\begin{equation}
\frac{\pi h}{6}(h^2+3r_2^2)
\end{equation}
も求まります。
逆に、球台は大きな球欠から小さな球欠を取り除いてできた図形です。
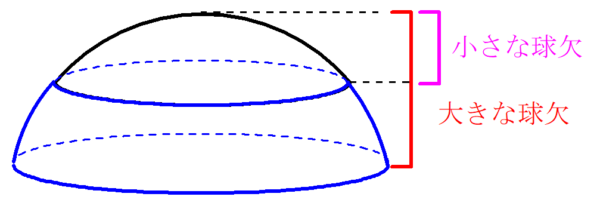
この考え方をもとに証明をしてみましょう。
もとの球の半径を $R~$とする。
球台の体積は、切り口の円の半径$~r_2~$、切り口の円の中心から球冠までの距離$~h_2~$の球欠の体積から、切り口の円の半径$~r_1~$、切り口の円の中心から球冠までの距離$~h_1~$の球欠の体積を引くことで求められる。
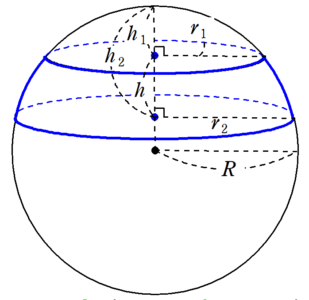
よって、球台の体積は、
\begin{equation}
\frac{\pi h_2}{6}(3r_2^2+h_2^2)-\frac{\pi h_1}{6}(3r_1^2+h_1^2) \\
\\
\end{equation}
と表せる。
$~h_2~$を消去するために、$~h_2=h+h_1~$を代入することで、
\begin{align}
&~~~\frac{\pi}{6}(h+h_1)\{3r_2^2+(h+h_1)^2\}-\frac{\pi h_1}{6}(3r_1^2+h_1^2) \\
\\
&=\frac{\pi}{6}(h+h_1)(3r_2^2+h_1^2+2hh_1+h^2)-\frac{\pi h_1}{6}(3r_1^2+h_1^2) \\
\\
&=\frac{\pi}{6}\left( 3h_1r_2^2+h_1^3+2hh_1^2+h^2h_1+3hr_2^2+hh_1^2+2h^2h_1+h^3-3h_1r_1^2-h_1^3 \right) \\
\\
&=\frac{\pi}{6}\left( h^3+3h_1r_2^2+3hh_1^2+3h^2h_1+3hr_2^2-3h_1r_1^2 \right) \\
\\
&=\frac{\pi}{6}\left\{ h^3+3\left( h_1r_2^2+hh_1^2+h^2h_1-h_1r_1^2 \right)+3hr_2^2 \right\} ~~~\cdots ① \\
\end{align}
\begin{align}
&~~~\frac{\pi}{6}(h+h_1)\{3r_2^2+(h+h_1)^2\}-\frac{\pi h_1}{6}(3r_1^2+h_1^2) \\
\\
&=\frac{\pi}{6}(h+h_1)(3r_2^2+h_1^2+2hh_1+h^2)\\
&~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~-\frac{\pi h_1}{6}(3r_1^2+h_1^2) \\
\\
&=\frac{\pi}{6}\left( 3h_1r_2^2+h_1^3+2hh_1^2+h^2h_1+3hr_2^2+hh_1^2 \right.\\
&~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\left. +2h^2h_1+h^3-3h_1r_1^2-h_1^3 \right) \\
\\
&=\frac{\pi}{6}\left( h^3+3h_1r_2^2+3hh_1^2+3h^2h_1+3hr_2^2-3h_1r_1^2 \right) \\
\\
&=\frac{\pi}{6}\left\{ h^3+3\left( h_1r_2^2+hh_1^2+h^2h_1-h_1r_1^2 \right)+3hr_2^2 \right\} \\
&~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\cdots ① \\
\end{align}
と式変形できる。
次に、$~h_1~$を消去するため、下の図の直角三角形に注目する。
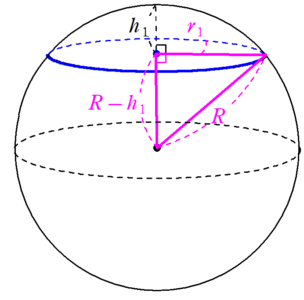
三平方の定理を使うと、
\begin{align}
R^2&=(R-h_1)^2+r_1^2 \\
R^2&=R^2-2Rh_1+h_1^2+r_1^2 \\
2Rh_1&=h_1^2+r_1^2 \\
R&=\frac{h_1^2+r_1^2}{2h_1}~~~~\cdots ②\\
\end{align}
と表せる。
同様に、球台の底面の半径$~r_2~$の円についても、
\begin{equation}
R=\frac{h_2^2+r_2^2}{2h_2}~~~~\cdots ③\\
\end{equation}
なので、$②$と$③$より、
\begin{align}
\frac{h_1^2+r_1^2}{2h_1}&=\frac{h_2^2+r_2^2}{2h_2} \\
\\
\frac{h_1^2+r_1^2}{h_1}&=\frac{h_2^2+r_2^2}{h_2} \\
\end{align}
となる。
この式に、$~h_2=h+h_1~$を代入することで、
\begin{align}
\frac{h_1^2+r_1^2}{h_1}&=\frac{(h+h_1)^2+r_2^2}{h+h_1} \\
\\
(h+h_1)(h_1^2+r_1^2)&=h_1 \left( h^2+2hh_1+h_1^2+r_2^2 \right) \\
\\
hh_1^2+hr_1^2+h_1^3+h_1r_1^2&=h^2h_1+2hh_1^2+h_1^3+h_1r_2^2 \\
\\
hr_1^2&=h_1r_2^2+hh_1^2+h^2h_1-h_1r_1^2 ~~~\cdots ④\\
\end{align}
という式が求まる。
この$④$を$①$に代入することで、球台の体積は、
\begin{align}
&~~~\frac{\pi}{6}\left( h^3+3\cdot hr_1^2 +3hr_2^2 \right) \\
\\
&=\frac{\pi h}{6}\left( h^2+3r_1^2 +3r_2^2 \right) \\
\end{align}
と求まった。$~~~\blacksquare~$
$①$と$④$の式が繋がったときは感動しましたが、もっと簡単に計算する方法があるはず・・・。
ま、とりあえずは証明できました。
Ⅲ 球帯の面積
次に球帯の面積ですが、こちらに関しては、もとの球の半径$~R~$を使った方がきれいにまとまります。

上図のような、天面と底面の距離が$~h~$、もとの球の半径が$~R~$である球台の体積は、
\begin{equation}
2\pi Rh
\end{equation}
と表せる。
この式は、「球冠の面積」の最後で紹介した式と全く同じです。
球帯の面積は、もとの球から切断するときの厚さ$~h~$に比例する
と言うことができます。
また、これまでの球欠や球台の体積、球冠の面積と同じように、$~r_1~,~r_2~,~h~$のみで表したかったのですが、それを試みると、次のような式になります。
\begin{equation}
\pi \sqrt{h^4+r_1^4+r_2^4+2h^2r_1^2-2r_1^2r_2^2+2r_2^2h^2}
\end{equation}
非常に長いですね。$~(a+b+c)^2~$の形になりそうでならないのが惜しい・・・。
というわけで、今回はやむなく$~R~$を使って公式を提示したわけです。
証明は球冠の面積の公式を使えば、非常に簡単です。
もとの球の半径を $R~$とする。
球帯の面積は、切り口の円の中心から球冠までの距離$~h_2~$の球冠の面積から、切り口の円の中心から球冠までの距離$~h_1~$の球冠の面積を引くことで求められる。
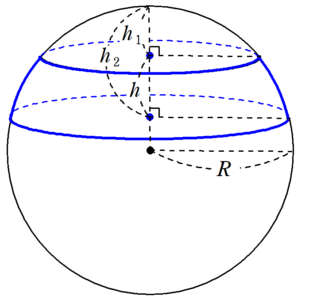
よって、球帯の面積は、
\begin{align}
&~~~2\pi Rh_2-2\pi Rh_1 \\
&=2\pi R(h_2-h_1) \\
&=2\pi R h
\end{align}
と求まった。$~~~\blacksquare~$
ということで、簡単に求まりました。
そもそも球冠が$~h~$に比例するので、当たり前っちゃ当たり前ですね。
前記事の「球欠」に比べて「球台」は複雑でした。

◇参考文献等
・「球欠と球冠-大学入試問題」,<http://sshmathgeom.private.coocan.jp/problem/Archimedes24.html > 2020年8月14日アクセス
・「いらすとや」,<https://www.irasutoya.com/2018/12/blog-post_66.html> 2020年8月14日アクセス

コメント