未分類– category –
未分類
-

メナイクモスが円錐曲線を導入!立方体倍積問題の解法を解説!【数学史6-19】
この記事では、古代ギリシャの数学者メナイクモスが立方体倍積問題を解くために円錐曲線を初めて使用したことを解説しています。メナイクモスは平面を異なる角度で切断することで、放物線、楕円、双曲線などを生み出し、これらを用いて立方体の体積を倍にする問題に取り組みました。 -

【まとめ】三角比の値~マイナーな角度の三角比まで表形式で紹介~
0°から90°までの三角比の値。数学Ⅰで学ぶのは0°、30°、45°、60°、90°の5つです。しかし、これらの角以外にも小数を使わずに正確な値を出せる角度があります。それらの値について、表形式でまとめました。リンク先の個別ページでは、値の出し方まで解説しています。 -

倍数判定法~7の倍数や11の倍数にも見分け方はある!? 証明含めて様々な倍数判定法を解説~
2の倍数かどうかは下1桁で、3の倍数かどうかは各桁の和でわかりますが、7の倍数や11の倍数はどう判定するのでしょうか? 各判定法の証明や必ず覚えるべきものを現役数学教員が解説。必要な判定法を覚えて、約分や素因数分解を効率的に行えるようになりましょう。 -

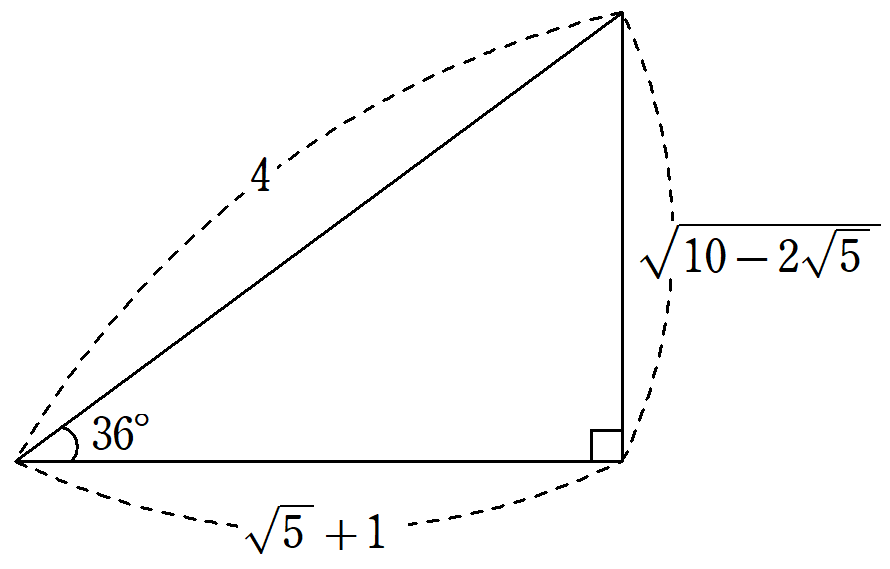
正五角形の作図方法~コンパスと定規による書き方を解説!なぜ書けるのかまで証明!~
1つの内角が108°という半端な角を持つ正五角形。一辺と対角線の長さの比は、無理数が登場する黄金比であるにも関わらず、定規とコンパスだけで作図をすることができます。作図方法を解説するとともに、なぜその方法で作図ができるのかを三平方の定理から証明します。 -

正五角形と黄金比~正五角形の対角線の性質を解説!含まれる二等辺三角形の個数は?~
1つの内角が108°という半端な角を持つ正五角形。しかし、正五角形の一辺と対角線の比は、昔から人々が魅了されている「黄金比」となります。この記事では、実際にその比を求めるだけでなく、あまり知られていない正五角形と黄金比の関係について解説。黄金三角形を知っていますか? -

私学適性(数学)令和3年度解説 大問2
東京都私学教員適性検査の過去問(令和3年度)の答えを解説付きで載せています。問題集の解答例で、解法を調べたい際にご活用ください。大問1大問2(本ページ)※大... -

私学適性(数学)令和3年度解説 大問1
東京都私学教員適性検査の過去問(令和3年度)の答えを解説付きで載せています。問題集の解答例で、解法を調べたい際にご活用ください。大問1(本ページ)大問2※大... -

【数学史4-1】インド数学も古代では未発展?その歴史とブラーフミー数字について解説!
数学と言えばインドですが、紀元前におけるインドは同じ四大文明のエジプト、メソポタミア、中国と比べて数学的な面で劣っていました。その理由を古代インドの歴史から考察すると共に、現代のアラビア数字につながる、古代インドの偉大な発明「ブラーフミー数字」の表し方を解説します。 -

私学適性(数学)令和2年度解説 大問2
東京都私学教員適性検査の過去問(令和2年度)の答えを解説付きで載せています。問題集の解答例で、解法を調べたい際にご活用ください。大問1大問2(本ページ)※大... -

私学適性(数学)令和2年度解説 大問1
東京都私学教員適性検査の過去問(令和2年度)の答えを解説付きで載せています。問題集の解答例で、解法を調べたい際にご活用ください。大問1(本ページ)大問2※大...