2023年5月23日、高校生4人が円周率の新しい求め方を証明したという記事 が、神戸新聞より掲載されました。
しかし、その高校生たちが英語で書いた論文のタイトルは「円に内接する多角形の中で、面積が最大になるのは正多角形であることの初等的な証明」となっています。
メディアの取り上げ方には疑問が残りますが、高校生が高校数学のみを使って証明していることが画期的な論文です。
この記事では、その論文の内容をざっくりと解説!
メディアの誇張に騙されないよう、論文の中身を大まかに理解しましょう。
なぜ話題となっているのか?
5月末様々なニュースサイトで取り上げられていたため、記憶に残っている人も多いでしょう。
これほどまでに話題になっている要因は、以下の3つによるものかと思います。
- 高校生が高校以下の数学で証明したから。
- オーストラリアの研究誌に特集されたから。
- メディアが「円周率」という言葉を使ったから。
1つ1つの要因を詳しく見てみましょう。
高校生が高校以下の数学で証明したから
今回論文を提出したのは、兵庫県の高校生4人と彼らを指導した教諭1人。
その教諭は「私がほとんど口を挟むことなくやってのけた」とインタビューに答えているため、4人の高校生が書いた論文として話題になっています。

論文の中では「高校生でもわかる」という表現が幾度か出てきており、実際の内容も基本的な幾何の性質に加え、数列や極限といった高校数学までの知識のみを確かに使っているため、エレガントな証明として話題を集めています。
オーストラリアの研究誌に特集されたから
今回の論文は、オーストラリアの国立ニューサウスウェールズ大学(UNSW)で、50年以上続く数学雑誌『Parabola』の特集記事として取り上げられました。
学生向けの雑誌とはいえ、歴史ある海外の学術誌に特集されたことで、今回の論文が国境を越えて影響を与えています。
メディアが「円周率」という言葉を使ったから
今回のニュースで疑問に残るのは、円周率の求め方に関する記述が無いにも関わらず、ニュースのタイトルに「円周率の新しい求め方」という表現が入っている点です。
確かに、円内部の正多角形によって円周率を求めていく方法は存在しますが、今回の論文の内容には直接関係はなく、その方法は古代エジプトから存在している歴史の長い方法です。

「円周率の新しい求め方』といニュースタイトルは、メディアが万人向けに、証明の話題性を誇張するためにつけた表現と推測されます。
論文の内容
高校生4人が書いた今回の論文は、以下のタイトルと5つの章から構成されています。
「円に内接する多角形の中で、面積が最大になるのは正多角形であることの初等的な証明」
(An elementary proof that the regular polygon is the largest among polygons that are inscribed in a circle)
- 序文
(Introduction) - 偶数本の辺を持つ多角形の面積
(The area of polygons with an even number of sides) - 任意の本数の辺を持つ多角形
(Polygons with arbitrarily many sides) - 異なる水量の容器に関する問題
(A problem of containers with different water levels) - 付録
(Appendix)
それぞれに出てくる注目すべき定義や定理を紹介しつつ、どのような流れで論じられているのかをざっくり解説していきます。
1章 序文
次のような2行から、論文が始まります。
この論文では、次の事実の初等的な証明を与えている。
(*) 円に内接する多角形の中で、正多角形は最大の面積を持つ
この論文で証明したいことがまず述べられています。
ご覧の通り、円周率の新しい求め方に関する論文ではないことがわかるでしょう。
1章では、その後の各章でどんなことが述べられているかを大まかに紹介していますが、あらゆるところで出てくるのが「この論文の証明は高校生でも理解できる」という主張。

それこそがこの論文の画期的な点であり、4人の高校生たちがアピールしたいポイントであることがわかる序文となっています。
2章 偶数本の辺を持つ多角形の面積
まずは辺の数が偶数のときの多角形について考えています。
鍵となるのは、定義1に出てくる数列の2種類の変換方法です。
有限な数列$~a_1~,~a_2~,\cdots,~a_{2n}~$を、
\frac{a_{1}+a_{2}}{2}~,~\frac{a_{1}+a_{2}}{2}~,\frac{a_{3}+a_{4}}{2}~,\cdots,~\frac{a_{2n-1}+a_{2n}}{2}~,~\frac{a_{2n-1}+a_{2n}}{2}と変換することを 操作(a) と定義する。
また、有限な数列$~a_1~,~a_2~,\cdots,~a_{2n}~$を、
\frac{a_{2n}+a_{1}}{2}~,~\frac{a_{2}+a_{3}}{2}~,\frac{a_{2}+a_{3}}{2}~,\cdots,~\frac{a_{2n-2}+a_{2n-1}}{2}~,~\frac{a_{2n}+a_{1}}{2}と変換することを 操作(b) と定義する。
2つの操作(a)(b)を定義したうえで、次の 定理2 がこの章の主題となっています。
$~2~$以上の自然数$~n~$に対し、円に内接する$~2n~$角形の中で、正$~2n~$角形は最大の面積を持つ。
2章では、この定理の証明を約2ページ半かけて行っています。
具体的には、任意の内接多角形の中心角に操作(a)と操作(b)を交互に適用していくことで、その多角形の面積を拡大させながら、正多角形に収束させていくという方法をとっています。
序文でも主張されていたように、計算こそ複雑で説明も長くなっていますが、数学Ⅲの極限までの知識で理解することができます。
ここでは、実際に操作(a)と操作(b)により、多角形が面積を拡大させながら正多角形になるのかを具体例で示したいと思います。
円に内接する六角形$~P_1P_2P_3P_4P_5P_6~$で考える。
中心角をそれぞれ
\theta_1=30^{\circ}~,\theta_2=70^{\circ}~,\theta_3=40^{\circ}~,\theta_4=80^{\circ}~,\theta_5=90^{\circ}~,\theta_6=50^{\circ}とする。

これらの角に 操作(a) を行うと、
\gamma_1=50^{\circ}~,\gamma_2=60^{\circ}~,\gamma_3=70^{\circ}となる。

このとき、$~\triangle P_1P_2P_3~$と$~\triangle Q_1Q_2Q_3~$を比較すると、$~\triangle Q_1Q_2Q_3~$の高さは$~P_1P_3~(=Q_1Q_3)~$の垂直二等分線なので、$~P_1P_3~$を底辺とする内接三角形の中で$~\triangle P_1Q_2P_3~(=\triangle Q_1Q_2Q_3)~$が最大となる。
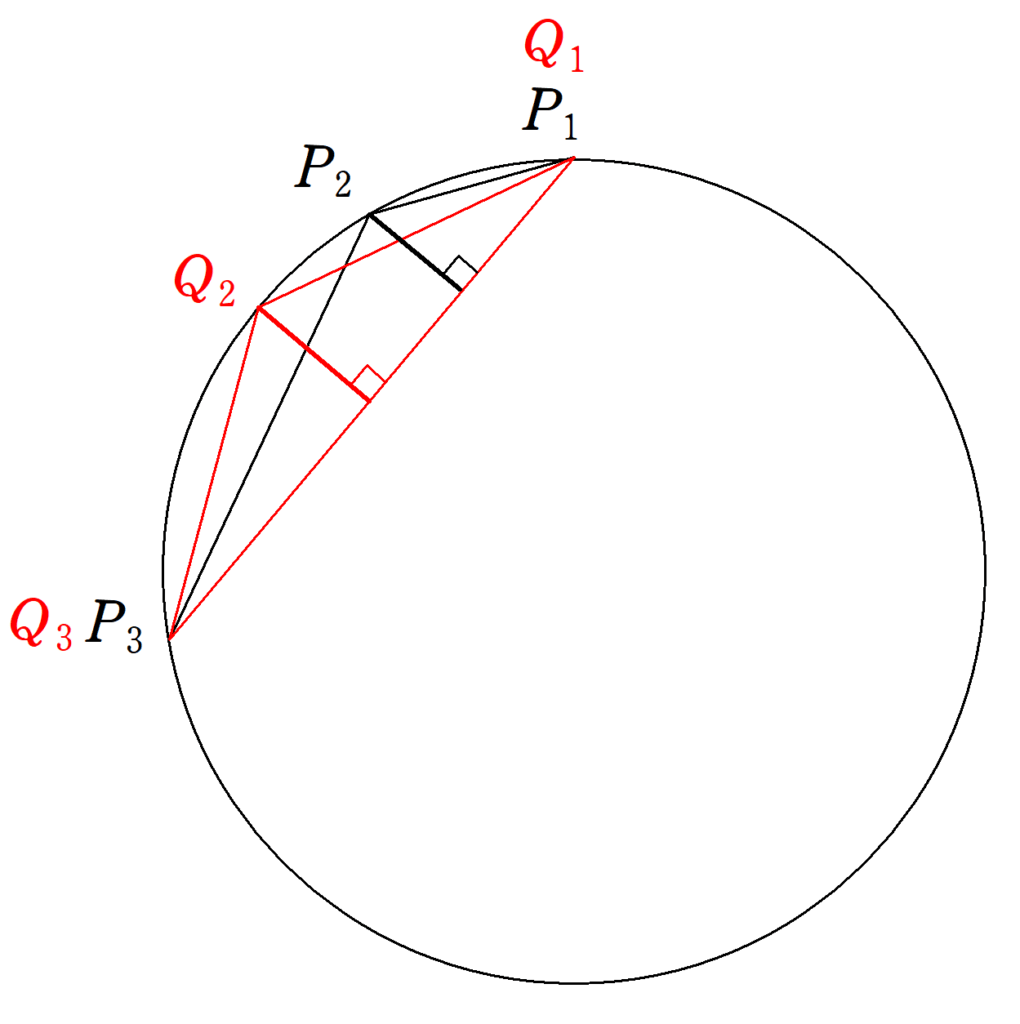
六角形$~Q_1Q_2Q_3Q_4Q_5Q_6~$の中心角
50^{\circ}~,~50^{\circ}~,~60^{\circ}~,~60^{\circ}~,~70^{\circ}~,~70^{\circ}に操作(b)を行うと、
\beta_{1,1}=60^{\circ}~,~\beta_{1,2}=55^{\circ}~,~\beta_{1,2}=55^{\circ}~,~\beta_{1,3}=65^{\circ}~,~\beta_{1,3}=65^{\circ}~,~\beta_{1,1}=60^{\circ}となる。

六角形$~R_1R_2R_3R_4R_5R_6~$の中心角
60^{\circ}~,~55^{\circ}~,~55^{\circ}~,~65^{\circ}~,~65^{\circ}~,~60^{\circ}に操作(a)を行うと、
\beta_{2,1}=57.5^{\circ}~,~\beta_{2,1}=57.5^{\circ}~,~\beta_{2,2}=60^{\circ}~,~\beta_{2,2}=60^{\circ}~,~\beta_{2,3}=62.5^{\circ}~,~\beta_{2,3}=62.5^{\circ}となる。

確かに操作(a)と操作(b)を交互に繰り返すことで、中心角が$~60^{\circ}~$に近づいていることがわかります。
中心角が$~60^{\circ}~$になるということは、すなわち正六角形になることを意味し、STEP1の議論から、作業をすればするほど面積も大きくなっています。
実際、操作(a)と操作(b)を10回ずつ繰り返したとき、6つの中心角と六角形の面積は次のように変化します。
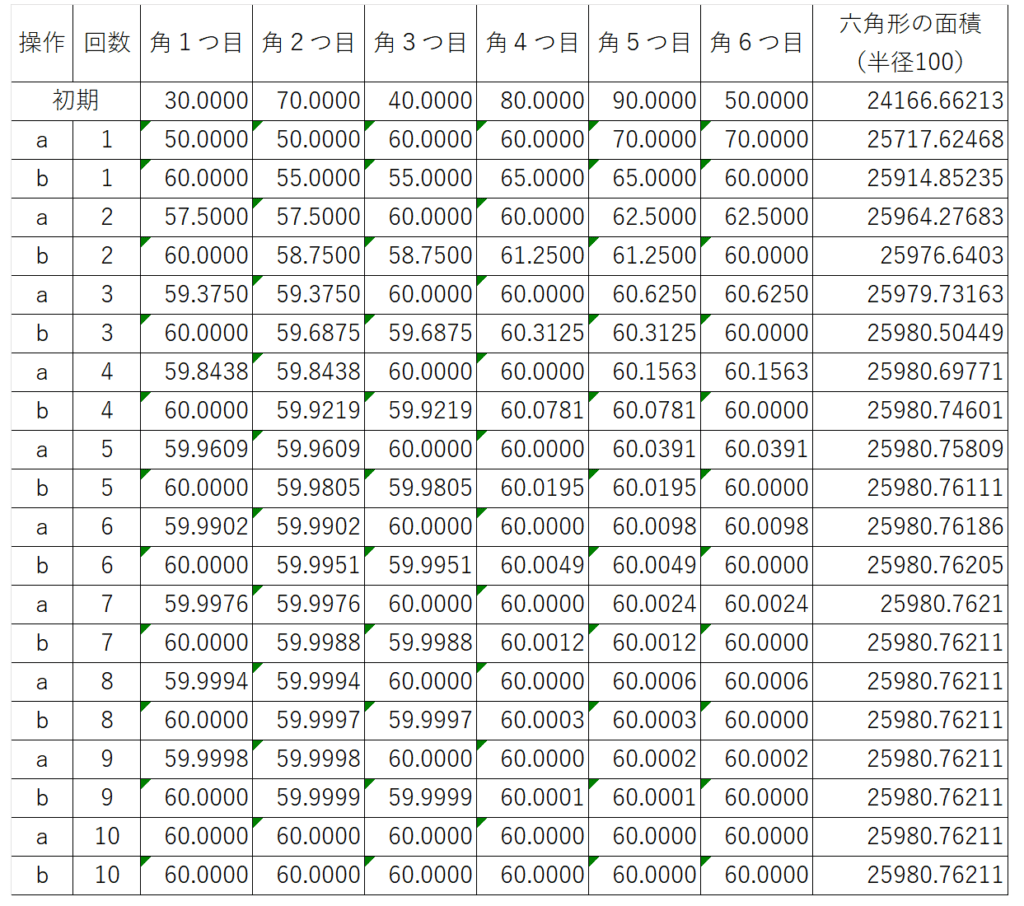
小数第4位まで求めていますが、操作(a)10回目の時点ですべての角が$~60.0000^{\circ}$となっているのがわかるでしょう。
確かに中心角は$~60^{\circ}$に収束、六角形の面積は
\frac{1}{2}\cdot 100 \cdot 100 \cdot \sin{60^{\circ}} \cdot 6=15000\sqrt{3} \fallingdotseq25980.76211へと収束しています。
論文では、数学Ⅲまでの知識である不等式や級数を使って証明しています。
3章 任意の本数の辺を持つ多角形
操作(a)や操作(b)は偶数項の数列でしか使えません。
そこで、奇数本の辺を持つ多角形でも証明をするため、この章では操作(c)を定義しています。
有限な数列$~b_1~,~b_2~,\cdots,~b_{n}~$を、任意の$~1 \leqq i < n~$について、
b_1~,~b_2~,\cdots,~b_{i-1}~,~\frac{b_{i}+b_{i+1}}{2}~,\frac{b_{i}+b_{i+1}}{2}~,~b_{i+2}~,\cdots,b_{n}と変換することを 操作(c) と定義する。
この操作(c)の意味は4章で水を例にわかりやすく説明されています。
3章の主題は、操作(c)を利用した次の定理5の証明です。
数列$~a_1~,~a_2~,~\cdots~,a_n~$$~(a_1+a_2+\cdots+a_n=s)~$に、操作(c)をすべての$~i=1~,2~,\cdots,n~$に繰り返し適用することで、元の数列は
\frac{s}{n}~,~\frac{s}{n}~,~\cdots~,~\frac{s}{n} に収束する。
操作(c)の説明では$~1 \leqq i < n~$、この定理5では$~i=1~,2~,\cdots,n~$となっており、特に注意書きは無かったものの、操作(b)に倣って$~i=n~$のときは、
\frac{b_1+b_n}{2}~,~b_2~,~b_3~,~\cdots~,~b_{n-1}~,~\frac{b_1+b_n}{2}という理解で良いのかなと思います。
定理5の意味としては、どんな多角形だとしても中心角に操作(c)を繰り返すことで正多角形につながるということを表しています。


証明は数学的帰納法で行われており、最終的には極限によって各項が$~\displaystyle \frac{s}{n}~$に収束することを示しています。
2章で正多角形に近づくほど、面積も大きくなることを示していたため、定理5の証明完了と共に論文のタイトルである定理7が示されました。
任意の$~3~$以上の整数$~n~$に対し、正$~n~$角形は円に内接する$~n~$角形の中で最大の面積を持つ。
4章 異なる水量の容器に関する問題
操作(c)によって数列の各項が、平均に近づいていく様子を具体例で表しているのが4章です。
論文でも10個の容器を使って説明していますが、同様の説明を5つの容器で簡単に考えてみます。
水量がそれぞれ$~a_1~,~a_2~,~a_3~,~a_4~,~a_5~$の5つのビーカーがある。
-1024x473.png)
ここに、$~i=3~$における操作(c)を適用すると、
a_1~,~a_2~,~\frac{a_3+a_4}{2}~,~\frac{a_3+a_4}{2}~,~a_5となる。
-1024x473.png)
この操作を各隣接する容器で行っていけば、どの容器の水量もいずれは同じになることがわかるでしょう。
実際、中心角が$~50^{\circ}~,~70^{\circ}~,~110^{\circ}~,~30^{\circ}~,~100^{\circ}~$の五角形に、操作(c)をランダムな$~i~$について実行したら、90回目ですべての角が$~72.0000^{\circ}~$となりました。
操作(c)を90回行った結果を見る
| 操作回数 | i | 容器1 | 容器2 | 容器3 | 容器4 | 容器5 |
| 初期 | 50 | 70 | 110 | 30 | 100 | |
| 1 | 2 | 50 | 90 | 90 | 30 | 100 |
| 2 | 3 | 50 | 90 | 60 | 60 | 100 |
| 3 | 3 | 50 | 90 | 60 | 60 | 100 |
| 4 | 1 | 70 | 70 | 60 | 60 | 100 |
| 5 | 5 | 85 | 70 | 60 | 60 | 85 |
| 6 | 2 | 85 | 65 | 65 | 60 | 85 |
| 7 | 4 | 85 | 65 | 65 | 72.5 | 72.5 |
| 8 | 3 | 85 | 65 | 68.75 | 68.75 | 72.5 |
| 9 | 1 | 75 | 75 | 68.75 | 68.75 | 72.5 |
| 10 | 5 | 73.75 | 75 | 68.75 | 68.75 | 73.75 |
| 11 | 1 | 74.375 | 74.375 | 68.75 | 68.75 | 73.75 |
| 12 | 5 | 74.0625 | 74.375 | 68.75 | 68.75 | 74.0625 |
| 13 | 2 | 74.0625 | 71.5625 | 71.5625 | 68.75 | 74.0625 |
| 14 | 5 | 74.0625 | 71.5625 | 71.5625 | 68.75 | 74.0625 |
| 15 | 3 | 74.0625 | 71.5625 | 70.1563 | 70.1563 | 74.0625 |
| 16 | 5 | 74.0625 | 71.5625 | 70.1563 | 70.1563 | 74.0625 |
| 17 | 1 | 72.8125 | 72.8125 | 70.1563 | 70.1563 | 74.0625 |
| 18 | 5 | 73.4375 | 72.8125 | 70.1563 | 70.1563 | 73.4375 |
| 19 | 5 | 73.4375 | 72.8125 | 70.1563 | 70.1563 | 73.4375 |
| 20 | 4 | 73.4375 | 72.8125 | 70.1563 | 71.7969 | 71.7969 |
| 21 | 4 | 73.4375 | 72.8125 | 70.1563 | 71.7969 | 71.7969 |
| 22 | 4 | 73.4375 | 72.8125 | 70.1563 | 71.7969 | 71.7969 |
| 23 | 4 | 73.4375 | 72.8125 | 70.1563 | 71.7969 | 71.7969 |
| 24 | 4 | 73.4375 | 72.8125 | 70.1563 | 71.7969 | 71.7969 |
| 25 | 3 | 73.4375 | 72.8125 | 70.9766 | 70.9766 | 71.7969 |
| 26 | 5 | 72.6172 | 72.8125 | 70.9766 | 70.9766 | 72.6172 |
| 27 | 2 | 72.6172 | 71.8945 | 71.8945 | 70.9766 | 72.6172 |
| 28 | 3 | 72.6172 | 71.8945 | 71.4355 | 71.4355 | 72.6172 |
| 29 | 5 | 72.6172 | 71.8945 | 71.4355 | 71.4355 | 72.6172 |
| 30 | 3 | 72.6172 | 71.8945 | 71.4355 | 71.4355 | 72.6172 |
| 31 | 2 | 72.6172 | 71.665 | 71.665 | 71.4355 | 72.6172 |
| 32 | 3 | 72.6172 | 71.665 | 71.5503 | 71.5503 | 72.6172 |
| 33 | 5 | 72.6172 | 71.665 | 71.5503 | 71.5503 | 72.6172 |
| 34 | 3 | 72.6172 | 71.665 | 71.5503 | 71.5503 | 72.6172 |
| 35 | 2 | 72.6172 | 71.6077 | 71.6077 | 71.5503 | 72.6172 |
| 36 | 2 | 72.6172 | 71.6077 | 71.6077 | 71.5503 | 72.6172 |
| 37 | 1 | 72.1124 | 72.1124 | 71.6077 | 71.5503 | 72.6172 |
| 38 | 5 | 72.3648 | 72.1124 | 71.6077 | 71.5503 | 72.3648 |
| 39 | 3 | 72.3648 | 72.1124 | 71.579 | 71.579 | 72.3648 |
| 40 | 3 | 72.3648 | 72.1124 | 71.579 | 71.579 | 72.3648 |
| 41 | 4 | 72.3648 | 72.1124 | 71.579 | 71.9719 | 71.9719 |
| 42 | 3 | 72.3648 | 72.1124 | 71.7754 | 71.7754 | 71.9719 |
| 43 | 2 | 72.3648 | 71.9439 | 71.9439 | 71.7754 | 71.9719 |
| 44 | 4 | 72.3648 | 71.9439 | 71.9439 | 71.8737 | 71.8737 |
| 45 | 4 | 72.3648 | 71.9439 | 71.9439 | 71.8737 | 71.8737 |
| 46 | 1 | 72.1544 | 72.1544 | 71.9439 | 71.8737 | 71.8737 |
| 47 | 5 | 72.014 | 72.1544 | 71.9439 | 71.8737 | 72.014 |
| 48 | 3 | 72.014 | 72.1544 | 71.9088 | 71.9088 | 72.014 |
| 49 | 4 | 72.014 | 72.1544 | 71.9088 | 71.9614 | 71.9614 |
| 50 | 3 | 72.014 | 72.1544 | 71.9351 | 71.9351 | 71.9614 |
| 51 | 4 | 72.014 | 72.1544 | 71.9351 | 71.9483 | 71.9483 |
| 52 | 4 | 72.014 | 72.1544 | 71.9351 | 71.9483 | 71.9483 |
| 53 | 3 | 72.014 | 72.1544 | 71.9417 | 71.9417 | 71.9483 |
| 54 | 3 | 72.014 | 72.1544 | 71.9417 | 71.9417 | 71.9483 |
| 55 | 1 | 72.0842 | 72.0842 | 71.9417 | 71.9417 | 71.9483 |
| 56 | 5 | 72.0162 | 72.0842 | 71.9417 | 71.9417 | 72.0162 |
| 57 | 4 | 72.0162 | 72.0842 | 71.9417 | 71.979 | 71.979 |
| 58 | 4 | 72.0162 | 72.0842 | 71.9417 | 71.979 | 71.979 |
| 59 | 1 | 72.0502 | 72.0502 | 71.9417 | 71.979 | 71.979 |
| 60 | 2 | 72.0502 | 71.9959 | 71.9959 | 71.979 | 71.979 |
| 61 | 5 | 72.0146 | 71.9959 | 71.9959 | 71.979 | 72.0146 |
| 62 | 2 | 72.0146 | 71.9959 | 71.9959 | 71.979 | 72.0146 |
| 63 | 5 | 72.0146 | 71.9959 | 71.9959 | 71.979 | 72.0146 |
| 64 | 2 | 72.0146 | 71.9959 | 71.9959 | 71.979 | 72.0146 |
| 65 | 5 | 72.0146 | 71.9959 | 71.9959 | 71.979 | 72.0146 |
| 66 | 4 | 72.0146 | 71.9959 | 71.9959 | 71.9968 | 71.9968 |
| 67 | 1 | 72.0053 | 72.0053 | 71.9959 | 71.9968 | 71.9968 |
| 68 | 2 | 72.0053 | 72.0006 | 72.0006 | 71.9968 | 71.9968 |
| 69 | 5 | 72.001 | 72.0006 | 72.0006 | 71.9968 | 72.001 |
| 70 | 1 | 72.0008 | 72.0008 | 72.0006 | 71.9968 | 72.001 |
| 71 | 4 | 72.0008 | 72.0008 | 72.0006 | 71.9989 | 71.9989 |
| 72 | 3 | 72.0008 | 72.0008 | 71.9997 | 71.9997 | 71.9989 |
| 73 | 4 | 72.0008 | 72.0008 | 71.9997 | 71.9993 | 71.9993 |
| 74 | 3 | 72.0008 | 72.0008 | 71.9995 | 71.9995 | 71.9993 |
| 75 | 1 | 72.0008 | 72.0008 | 71.9995 | 71.9995 | 71.9993 |
| 76 | 4 | 72.0008 | 72.0008 | 71.9995 | 71.9994 | 71.9994 |
| 77 | 4 | 72.0008 | 72.0008 | 71.9995 | 71.9994 | 71.9994 |
| 78 | 4 | 72.0008 | 72.0008 | 71.9995 | 71.9994 | 71.9994 |
| 79 | 3 | 72.0008 | 72.0008 | 71.9995 | 71.9995 | 71.9994 |
| 80 | 3 | 72.0008 | 72.0008 | 71.9995 | 71.9995 | 71.9994 |
| 81 | 1 | 72.0008 | 72.0008 | 71.9995 | 71.9995 | 71.9994 |
| 82 | 3 | 72.0008 | 72.0008 | 71.9995 | 71.9995 | 71.9994 |
| 83 | 1 | 72.0008 | 72.0008 | 71.9995 | 71.9995 | 71.9994 |
| 84 | 2 | 72.0008 | 72.0001 | 72.0001 | 71.9995 | 71.9994 |
| 85 | 3 | 72.0008 | 72.0001 | 71.9998 | 71.9998 | 71.9994 |
| 86 | 5 | 72.0001 | 72.0001 | 71.9998 | 71.9998 | 72.0001 |
| 87 | 2 | 72.0001 | 72 | 72 | 71.9998 | 72.0001 |
| 88 | 5 | 72.0001 | 72 | 72 | 71.9998 | 72.0001 |
| 89 | 4 | 72.0001 | 72 | 72 | 72 | 72 |
| 90 | 1 | 72 | 72 | 72 | 72 | 72 |
5章 付録
今回の定理「任意の$~3~$以上の整数$~n~$に対し、正$~n~$角形は円に内接する$~n~$角形の中で最大の面積を持つ」を、大学以上の数学によって示そうとした場合の証明方法が付録として載っています。
論文中の参考文献[2]を簡潔にまとめたもので、「コンパクト」や「有界閉集合」、「$~n~$次元ベクトル」といった高校数学では学ばない言葉も出てきています。
この章から、論文を書いた高校生たちの数学レベルの高さを窺い知れます。
まとめ:円周率とは関係ないが日本の未来を明るくするニュース
内容的には難しかったものの、レベルとしては高校数学で理解できる証明方法でした。
高校生が発見したということも、中心角を平均化していくという発想、それを水量で例えるわかりやすさが画期的だと思います。
円周率とは関係ないのは残念ですが、それはマスコミの誇張によるもの。
しかし、高校生たちの才能や数学への熱心さが日本の学術的未来を明るくしてくれるニュースでした。
参考文献
- 『An elementary proof that the regular polygon is the largest among polygons that are inscribed in a circle』,<https://www.parabola.unsw.edu.au/files/articles/2020-2029/volume-59-2023/issue-1/vol59_no1_7.pdf>,2023年6月8日アクセス
- Parabola,<https://www.parabola.unsw.edu.au/>,2023年6月8日アクセス
- 神戸新聞NEXT,<https://www.kobe-np.co.jp/news/hanshin/202305/0016385354.shtml>,2023年6月8日アクセス

コメント
コメント一覧 (8件)
質問です。
Oを中心とする円上に点ABCがこの順で存在し、角AOCのなす角が2θ (0<Θ<90度) を満たすとき、△OAC の面積は一定であることから、四角形OABCが面積最大となるのは、△ABCの面積が最大であるときで、ACが一定であることから、この時角AOB=角BOC=θ・①
5以上の自然数nにおいて、ある円Oに内接するn角形の、円に内接する点を順にa1,a2…anとする.
同じ円に内接するn角形としてこれが面積最大のとき、これが正多角形でないならば、角a(m-1)Oa(m)≠角a(m)Oa(m+1)を満たすmが存在することになるが、四角形Oa(m-1)a(m)a(m+1)の面積を考えれば、これは①と矛盾する。よって面積最大となるのは、正多角形。
nが3または4のときも正多角形が面積最大であることは求められる。
という証明じゃダメなんでしょうか?
つねきちかずきち。様
コメントありがとうございます。
確かに四角形$~oa_{m-1}a_{m}a_{m+1}~$の面積単体なら成り立つかとは思いますが、連続した四角形では言えないのかなと思いました。
$~oa_{m-1}a_{m}a_{m+1}+oa_{m}a_{m+1}a_{m+2}~$を考えた際に、重なっている部分がある以上、可能性を網羅しきれていないような気がします。
数学に関しては浅学ゆえ、ざっくりとした回答で申し訳ありません。
お忙しい中,ありがとうございました。それではこのまま動画は置いておくことにします。
(コメントではなく,お問い合わせに書くべき質問だったかもしれません。失礼しました。)
度々失礼します。ナコレコ数学劇場という名では検索しにくいことに気づきました。@nakorecomathという名のツイッターです。
返信ありがとうございました。正しいであろうと確認していただき安心しました。動画の証明を三角関数で表し整理したものは、ナコレコ数学劇場のツイッターに載せました。(リンクの貼り方がわからないので、これも探していただくしかないのですが。)設問を1つ付けた大学入試風の証明になりました。これも正しいか確認していただければ有難いです。
ナコレコ数学劇場様
ツイッターのほうも拝見いたしました。
補題の設定が美しいですね。
証明を読んでいて、特に気になる点はございませんでした。(あくまで素人目線ですが‥‥)
はじめまして【ナコレコ数学劇場】という名で10本ほど動画を作った者です。本名をお伝えすることもできるのですが,ネットの世界のしきたりをよく知らないので,とりあえずこの名でコメントいたします。高校生が発見したというニュースで,その発想は面白く拝見したのですが,高校生にわかる証明があまりないという部分について,こんな説明はないかと思い「【ナコレコ数学劇場】カナタくんでもわかる証明の巻」を作りました。そっとyoutubeに置いてあるだけなので,正しいことの検証を誰かにしてもらったわけではなく,どなたかに確認していただきたいと思い,こちらにコメントしました。ここにリンクを貼る方法もよくわからないので,検索していただくしかないのですが。よければよろしくお願いいたします。1週間前にツイッターに登録し,そこにもそっと置いてはあるのですが。
ナコレコ数学劇場様
コメントありがとうございます。
動画(https://www.youtube.com/watch?v=uriTiBXnlQM)を拝見いたしました。
直観的でわかりやすい説明でした!
ただ、厳密な証明となると、「同じ大きさの部分を互いに消し合って」を示すのが大変そうです。
今回の高校生の論文についても、やっていることは水の量を均すことと同じでわかりやすいものの、それを証明しようとすると、並の高校生では難しい議論をするため、わかりにくい内容となっています。
今後も動画のUP楽しみにしています!
じゃんけんの動画、面白かったです!
Fukusuke