【数学史２－５】古代エジプトの円周率は3.16！ 正方形から円の面積を近似する方法とは？

　幾何学の発祥地である古代エジプト。

　ナイル川が毎年氾濫し、土地の測量を毎年行っていた古代エジプトの人々にとって、円形の土地の面積を求める方法が必要でした。

　紀元前1650年頃に書かれた『リンド・パピルス』では、円周率を$~\displaystyle \frac{256}{81}\fallingdotseq 3.1604~$と算出しています。

　実は、この値は円の面積を9つの正方形を使って近似することで求められました。

　この記事では、その円周率の求め方について解説します。

円の面積を求める

　紀元前1650年頃に、古代エジプトの書記アーメスによって書かれた『リンド・パピルス』。

　そこに載っている円の面積を求める手順について見てみましょう。

直径 9 の円の面積は 64

　『リンド・パピルス』は問題集であったため、円に関しては次のような問題として載っていました。

　この問題には、次のような解法が載っていました。

　直径$~9~$の円の面積は、円周率を$~3.14~$として計算すると、

\frac{9}{2}\cdot \frac{9}{2}\cdot 3.14=63.585

となるため、$~64~$という答えがそこそこの精度を持っているとわかります。

古代エジプトの円周率は3.16

　『リンド・パピルス』問題50の計算結果から、古代エジプトの円周率を計算してみます。

　直径$~9~$の円の面積が$~64~$になるということは、円周率を$~p~$として、

\begin{align*}
\frac{9}{2}\cdot \frac{9}{2}\cdot p&=64  \\
\\
\frac{81}{4}p&=64  \\
\\
p&=\frac{256}{81}~~~\cdots①
\end{align*}

となります。

\frac{256}{81}\fallingdotseq3.1604938

であるため、$~\pi~$との誤差は$~0.02~$未満となっています。

　3500年以上も前から$~3.14~$に近い値が使われていたことに驚きですね。

円の面積は八角形から近似された

　直径$~9~$の円の面積が$~64~$になるという計算は、どのようにして生まれたのでしょうか。

『リンド・パピルス』問題48の図

　『リンド・パピルス』問題48には問題文が無く、次のような図だけが載っていました。

『リンド・パピルス』問題48

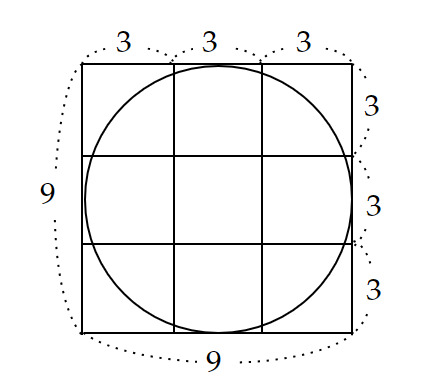
※$~3~$や$~9~$といった数字は書かれていなかった。

　この図から、直径$~9~$の円の面積を導くため、図2のような八角形を作ります。　

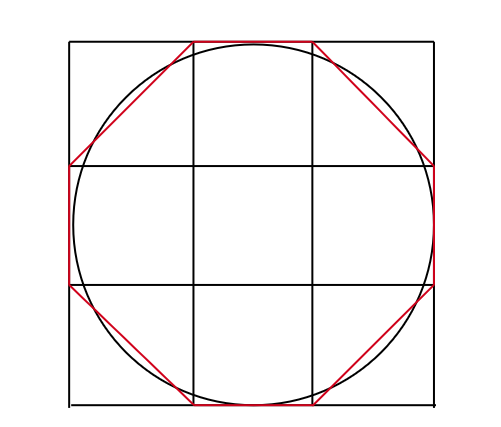
　図3より、この八角形の面積は円の面積とほぼ同じです。

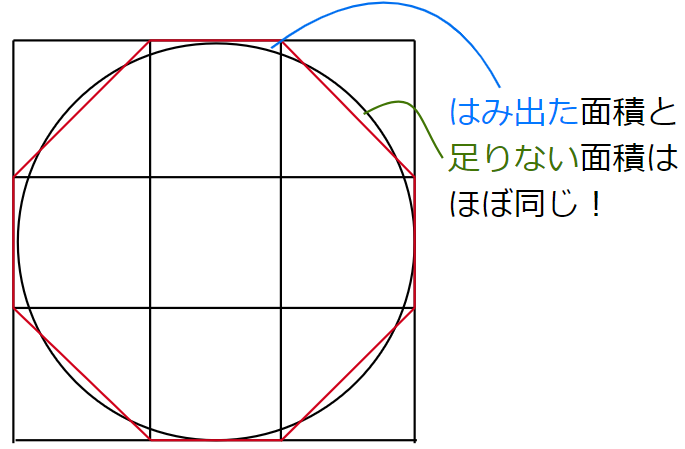
　そのため、八角形の面積を求めることで、直径$~9~$の円の面積の近似値が出せます。

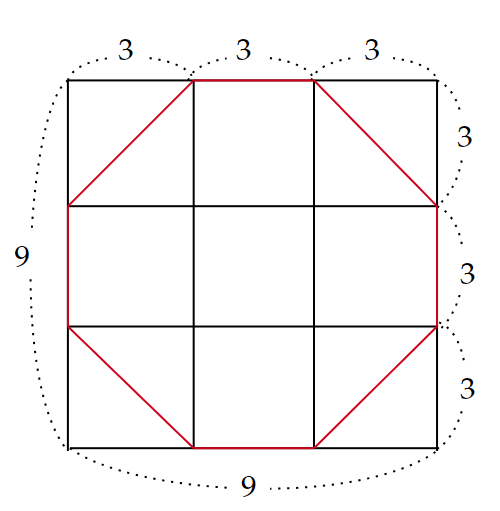
　正方形が5つ、直角二等辺三角形が4つであるため、

(3\cdot 3)\cdot 5+\left(3 \cdot 3 \cdot \frac{1}{2}\right)\cdot 4=63 

という値が出てきます。

63 より 64 のほうが都合が良い

　図4の八角形の面積によれば、直径$~9~$の円の面積は

9 \cdot 9 \cdot \frac{63}{81}=63 

と計算されるのが普通です。

　しかし、『リンド・パピルス』問題50では、円の面積は$~64~$としていました。

　その理由は、$~64~$が平方数だからです。

　アーメスをはじめとする古代エジプトの書記たちは、円に等しい面積を持つ正方形を求める問題（円積問題）に興味を持っていました。

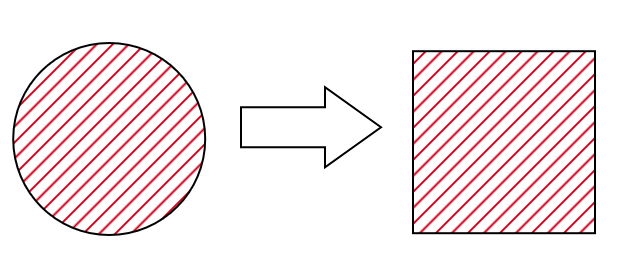
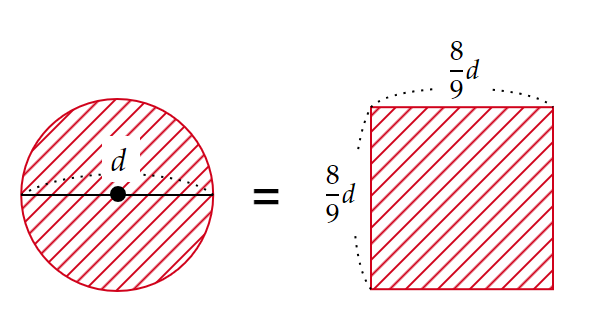
　これにより、直径$~d~$の円の面積は、$~\displaystyle \left(\frac{8}{9}d \right)^2~$、すなわち

直径の$~\displaystyle \frac{1}{9}~$を取り去った長さを2乗する

というアルゴリズムで求められるようになりました。

63 より 64 のほうが精度も良い

　直径$~9~$の円の面積を$~64~$と計算した場合、①より、円周率は$\displaystyle \frac{256}{81}\fallingdotseq 3.1604938~$（誤差は$~0.02~$未満）となりました。

　同じ計算方法で、面積が$~63~$の場合の円周率$~p~$を出してみましょう。

\begin{align*}
\frac{9}{2}\cdot \frac{9}{2}\cdot p&=63  \\
\\
\frac{81}{4}p&=63  \\
\\
p&=\frac{252}{81}  \\
\\
p&=\frac{28}{9}
\end{align*}

となり、

\frac{28}{9}\fallingdotseq3.1111111

です。

　$~\pi~$との誤差は$~0.03~$以上。
　偶然とは言え、$~64~$のほうが精度が良いことがわかります。

簡単な分数で円周率を表すこともあった

　円周率は$\displaystyle ~\frac{256}{81}\fallingdotseq 3.1604938~$でしたが、この数値を古代エジプトで表すためには苦労したはずです。

　その理由は、古代エジプトに小数はなく、分数、それも単位分数の和を使って表していたからです。

あわせて読みたい

【数学史２－４】古代エジプトの分数は単位分数！その利点とは？ 　古代エジプト文明における分数は、分子が 1 の単位分数と 3分の2 しかありませんでした。古代エジプト人が単位分数を好んだ理由は、生活上の「分ける」という観点で便利だったからです。この記事では、ヒエログリフやヒエラティックの分数の表し方から、9個のパンを10人で分ける問題の解き方まで解説します。

　実際、$\displaystyle ~\frac{256}{81}~$を単位分数の和で表すと、次のようになります。

\frac{256}{81}=3+\frac{1}{7}+\frac{1}{57}+\frac{1}{10773}

　計算上、とても実用的とは言えません。

　そのため、円周率として$~\displaystyle 3\frac{1}{6}\fallingdotseq 3.16666~$が使われていたという記録が、『カフーン・パピルス』などに残っています。

　ちなみに、古代ギリシャの数学者アルキメデス（Archimedes , B.C.287頃～B.C.212）は、正 96 角形を使って、円周率が約$~\displaystyle 3\frac{1}{7}~$であることを証明しました。

　同じ単位分数であれば、$~\displaystyle \frac{1}{6}~$より$~\displaystyle \frac{1}{7}~$のほうが近かったのは、バビロニア数学の惜しかった点です。

まとめ・参考文献

　古代エジプトの円周率について解説してきました。

• 古代エジプトの円周率は$~\displaystyle \frac{256}{81}\fallingdotseq 3.16~$。
• 円の面積は、八角形の面積をもとに算出された。
• 円に等しい面積を持つ正方形をつくる円積問題が、アーメスの思考の背景にあった。

　今から3500年以上も前から、曲線を直線で近似するという考え方があり、円周率が誤差$~0.02~$未満で求まっているのが驚きです。

　次の記事では、方程式をはじめとする、古代エジプトの有名問題について解説します。

次の記事へ

【数学史２－６】リンド・パピルスの有名問題を解説！方程式は仮置法で解ける！ 　古代エジプトの数学を知る上で、欠かせない資料が『リンド・パピルス』。「アハ問題」と呼ばれる方程式の問題やピラミッドの勾配の問題、等比数列の和の問題など、様々な分野の問題を扱っています。この記事では、その中でも有名な３つの問題を解説。今の数学でも使われたり、英語圏の童謡になっていたりと、現代にあらゆる形で残っています。

この章のまとめへ

【数学史まとめ２】古代エジプトの数学 　ナイル川の流域で、土地の測量から始まった古代エジプトの数学。その時代の数学を紐解く資料である『リンド・パピルス』には、象形文字を使って数学の問題と解説が書かれています。その内容としては、実生活に基づく問題が多く、古代エジプトの数学を特徴づけるものと言えるでしょう。この記事では、古代エジプトの数学に関する事柄を年表形式でまとめると共に、この時代の数学を大まかに解説します。

平方数へのこだわりが功を奏していたんだね

ちなみに円積問題は、1882年、円と同じ面積を持つ正方形はつくることができないということが証明され、解決に至ったよ。