Ⅰ 体積への拡張
一応最初なので、シンプソンの公式を復習しておきましょう。
$~f(x)~$ が3次以下の関数のとき、次の式が成り立つ。
\begin{equation}
\displaystyle \int_{a}^{b} f(x)dx=\frac{(b-a)}{6} \left\{ f(a)+4f\left( \frac{a+b}{2} \right) +f(b) \right\}
\end{equation}
\begin{align}
&\displaystyle \int_{a}^{b} f(x)dx \\
\\
&=\frac{(b-a)}{6} \left\{ f(a)+4f\left( \frac{a+b}{2} \right) +f(b) \right\}
\end{align}
証明や基本例は「シンプソンの公式(基本編)」を参照してください。
今回考えたいのは体積への応用です。高さが $~a~$ から $~b~$ までの範囲で、面積が3次以下の関数で増減するようであれば、シンプソンの公式で体積を求めることができます。
ということで、次章よりいくつか例を挙げていきます。説明をわかりやすくするため、次のような文字を使います。
$~xyz~$ 空間で、 $~f(z)~$ は高さ $~z~$ で切った立体の断面積とし、一番高いところを $~z=t~$ 、一番低いところを $~z=s~$ とすると、
求めたい体積は $~\displaystyle \int_{s}^{t}f(z)dz $と表せる。
また、立体の高さの半分の位置を $~\displaystyle \frac{t+s}{2}=m~$ としておく。
よって、シンプソンの公式で体積は次のように計算できる。
\begin{equation}
\displaystyle \frac{t-s}{6} \left\{ f(s)+ 4f(m) +f(t) \right\}
\end{equation}
では、シンプソンの公式の応用例を見ていきましょう。
Ⅱ 三角柱の体積
底辺が $~a~$ 、高さが $~b~$ の三角形を底辺にもつ、高さ $~h~$ の三角柱の体積
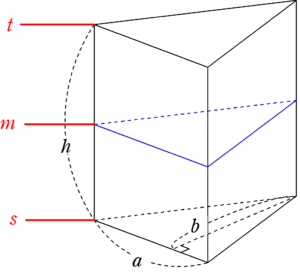
情報を整理する。
\begin{align}
\displaystyle f(t)&=\frac{ab}{2} \\
\\
f(s)&=\frac{ab}{2} \\
\\
f(m)&=\frac{ab}{2} \\
\\
t-s&=h
\end{align}
さらに、面積の増減は一定であるため、3次以下。
以上より、体積は
\begin{align}
&\displaystyle \frac{t-s}{6} \left\{ f(s)+ 4f(m) +f(t) \right\} \\
\\
&=\frac{h}{6} \left\{ \frac{ab}{2}+ 4\frac{ab}{2} +\frac{ab}{2} \right\} \\
\\
&=\frac{h}{6} \cdot 3ab \\
\\
&=\frac{abh}{2}
\end{align}
確かに、従来の方法で求めても同じ式が出てきます。
Ⅲ 円錐の体積
半径 $~r~$ の円を底面にもつ、高さ $~h~$ の円錐の体積
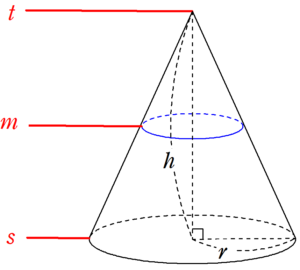
情報を整理する。
\begin{align}
\displaystyle f(t)&=0 \\
f(s)&=\pi r^2 \\
t-s&=h
\end{align}
相似から、 $~z=m~$ の面積は半径 $~\displaystyle \frac{r}{2}~$ の円なので、
\begin{align}
\displaystyle f(m)&=\pi \left( \frac{r}{2} \right)^2 \\
\\
&=\frac{\pi r^2}{4}
\end{align}
さらに、高さが $~\displaystyle \frac{1}{2}~$ 倍されれば、面積が $~\displaystyle \frac{1}{4}~$ 倍となっているので、面積の増減は2次関数的。
以上より、体積は
\begin{align}
&\displaystyle \frac{t-s}{6} \left\{ f(s)+ 4f(m) +f(t) \right\} \\
\\
&=\frac{h}{6} \left\{ \pi r^2 + 4\frac{\pi r^2}{4} + 0 \right\} \\
\\
&=\frac{h}{6} \cdot 2\pi r^2 \\
\\
&=\frac{\pi hr^2}{3}
\end{align}
確かに錐体は $~\displaystyle \frac{1}{3}~$ となっていますね!!
Ⅳ 四角錐台の体積
縦が $~a~$ 、横が $~b~$ の長方形を下底面に、縦が $~ap(0 < p < 1)~$ 、横が $~bp~$ の長方形を上底面にもつ、高さ $~h~$ の四角錐台の体積
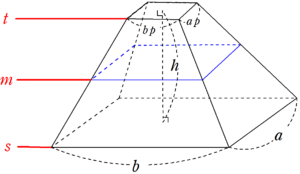
情報を整理する。
\begin{align}
\displaystyle f(t)&=abp^2 \\
f(s)&=ab \\
t-s&=h
\end{align}
$~z=m~$ の長方形の縦は $~\displaystyle \frac{ap+a}{2}~$ 、横は $~\displaystyle \frac{bp+b}{2}~$ なので、
\begin{align}
\displaystyle f(m)&=\frac{ap+a}{2} \cdot \frac{bp+b}{2}\\
\\
\displaystyle f(m)&=\frac{a(p+1)}{2} \cdot \frac{b(p+1)}{2}\\
\\
&=\frac{ab(p+1)^2}{4}
\end{align}
さらに、高さが $~p~$ 倍されれば、面積が $~p^2~$ 倍となっているので、面積の増減は2次関数的。
以上より、体積は
\begin{align}
&\displaystyle \frac{t-s}{6} \left\{ f(s)+ 4f(m) +f(t) \right\} \\
\\
&=\frac{h}{6} \left\{ ab + 4\frac{ab(p+1)^2}{4} + abp^2 \right\} \\
\\
&=\frac{h}{6} \left\{ ab+ab(p+1)^2+abp^2 \right\} \\
\\
&=\frac{abh}{6}(1+p^2+2p+1+p^2) \\
\\
&=\frac{abh}{3}(p^2+p+1) \\
\end{align}
複雑な錐台もバッチリ解けました。
シンプソンの公式、便利ですね。次回はもっと高度な図形に挑戦してみます!!

コメント
コメント一覧 (6件)
先生、こんばんは!!
わざわざまとめてくださり感涙です・・
おかげさまで完璧理解できました!
ありがとう、を何度も言わせてください!!
お忙しいところ、すみません。
いつも本当にありがとうございます!!
先生、おはようございます!
先日教えていただいたシンプソンの定理なのですが、
こちらの問題に当てはめると、どのように適用可能なのかが
うまくつかめませんでした・・
http://mathematics-monster.jp/PDF/3-8-3.pdf
図などございますと、とてもうれしいです^_^
ご返信お待ちしております!
適用可能ですよー。
シンプソンで解けました!
ただ、今週末にならないと、きちんと図を書いて説明できないので、少々お待ちくださいm(__)m
円錐を回転させる問題の答えができました。
拙筆申し訳ありません。
以下のpdfファイルをご確認ください。
円錐を回転させる問題の答え
お忙しいところ、ものすごくわかりやすい解説シートを書いてくださり、本当にありがとうございました!! 感謝の思いでいっぱいです(^^)