3次以下の関数の積分を求める際に使えるシンプソンの公式。まずは例と簡単な証明を与えます。
Ⅰ シンプソンの公式
Ⅱ 基本例
Ⅲ 反例
Ⅳ 証明1
Ⅰ シンプソンの公式
1743年、イギリスの数学者トーマス・シンプソンによって発表された、定積分の値を近似するための公式です。
$~f(x)~$ が3次以下の関数のとき、次の式が成り立つ。
\begin{equation}
\displaystyle \int_{a}^{b} f(x)dx=\frac{(b-a)}{6} \left\{ f(a)+4f\left( \frac{a+b}{2} \right) +f(b) \right\}
\end{equation}
\begin{align}
&\displaystyle \int_{a}^{b} f(x)dx \\
\\
&=\frac{(b-a)}{6} \left\{ f(a)+4f\left( \frac{a+b}{2} \right) +f(b) \right\}
\end{align}
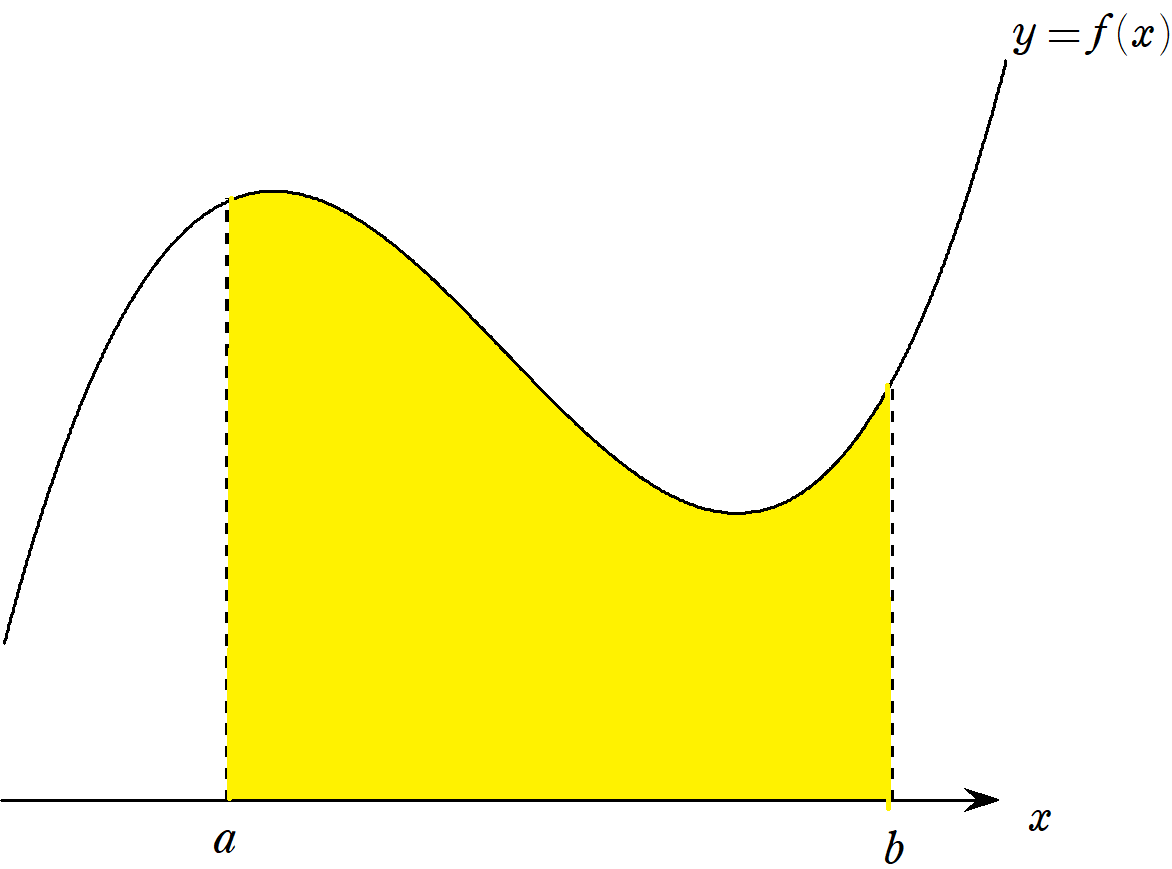
右辺がわかりづらいので、図から理解してみましょう。
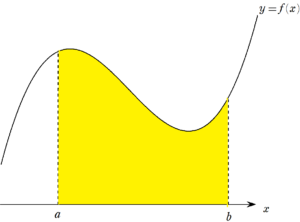
$~f(x)~$ を3次以下の関数としたとき、左辺の $~\displaystyle \int_{a}^{b} f(x)dx~$ は、下図の面積を求めることです。
次に、右辺を展開すると、
\begin{align}
\displaystyle &\frac{(b-a)}{6} \left\{ f(a)+4f\left( \frac{a+b}{2} \right) +f(b) \right\} \\
\\
&=\frac{(b-a)}{6} \cdot f(a)+4\frac{(b-a)}{6}\cdot f\left( \frac{a+b}{2} \right) +\frac{(b-a)}{6}\cdot f(b) \\
\end{align}
\begin{align}
\displaystyle &\frac{(b-a)}{6} \left\{ f(a)+4f\left( \frac{a+b}{2} \right) +f(b) \right\} \\
\\
&=\frac{(b-a)}{6} \cdot f(a)+4\frac{(b-a)}{6}\cdot f\left( \frac{a+b}{2} \right) \\
&+\frac{(b-a)}{6}\cdot f(b) \\
\end{align}
ですが、この $~\displaystyle \frac{(b-a)}{6}~$ というのは、区間 $~[a,b]~$ を6等分した長さとなります。
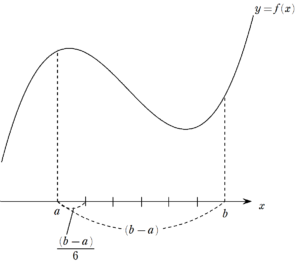
第2項は $~\displaystyle 4\frac{(b-a)}{6}~$ なので、6等分のうちの4区間分です。また、 $~\displaystyle f\left( \frac{a+b}{2} \right)~$ の $~\displaystyle \frac{a+b}{2}~$ は区間 $~[a,b]~$ の中点となります。
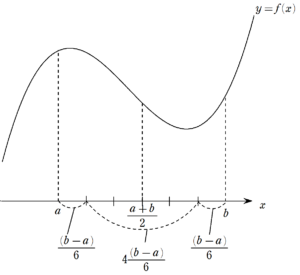
第1項全体の $~\displaystyle \frac{(b-a)}{6} \cdot f(a)~$ というのは、下図の赤い長方形の面積。
同様に、第2項は青色、第3項は緑色の長方形の面積を表しています。
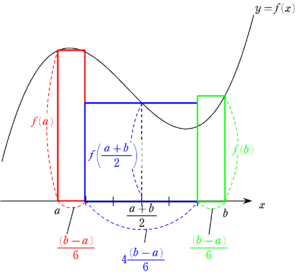
以上より、シンプソンの公式は関数で作られる面積を、
横の長さが $~1:4:1~$ の長方形3つで近似している
ということになります。
Ⅱ 基本例
実際に、いろいろな関数で試してみましょう。
・ $~\displaystyle \int_{2}^{4} -3x-2dx~$ を求める。
①まずは普通に計算した場合
\begin{align}
\displaystyle \int_{2}^{4} -3x-2dx&=\left[ -\frac{3}{2}x^2-2x \right]_{2}^{4} \\
\\
&=-24-8+6+4 \\
&=-22
\end{align}
②シンプソンの公式を使った場合
\begin{align}
f(2)&=-8 \\
f(4)&=-14 \\
\displaystyle f \left( \frac{2+4}{2} \right) &=f(3)=-11
\end{align}
よって、
\begin{align}
&\displaystyle \int_{2}^{4} -3x-2dx \\
\\
&=\frac{4-2}{6} \left\{ -8+4\cdot (-11)-14 \right\} \\
\\
&=\frac{1}{3} (-66) \\
\\
&=-22
\end{align}
シンプソンの公式のありがたみはあまりないですが、1次関数では結果が一致することがわかりました。
・ $~\displaystyle \int_{1}^{4} x^2-x+1 dx~$ を求める。
①まずは普通に計算した場合
\begin{align}
\displaystyle \int_{1}^{4} x^2-x+1 dx&=\left[ \frac{1}{3}x^3-\frac{1}{2}x^2+x \right]_{1}^{4} \\
\\
&=\frac{64}{3}-8+4-\frac{1}{3}+\frac{1}{2}-1 \\
\\
&=\frac{33}{2}
\end{align}
\begin{align}
&\displaystyle \int_{1}^{4} x^2-x+1 dx \\
\\
&=\left[ \frac{1}{3}x^3-\frac{1}{2}x^2+x \right]_{1}^{4} \\
\\
&=\frac{64}{3}-8+4-\frac{1}{3}+\frac{1}{2}-1 \\
\\
&=\frac{33}{2}
\end{align}
②シンプソンの公式を使った場合
\begin{align}
f(1)&=1 \\
f(4)&=13 \\
\displaystyle f \left( \frac{1+4}{2} \right) &=f\left( \frac{5}{2} \right)=\frac{19}{4}
\end{align}
よって、
\begin{align}
&\displaystyle \int_{1}^{4} -3x-2dx \\
\\
&=\frac{4-1}{6} \left( 1+4\cdot \frac{19}{4}+13 \right) \\
\\
&=\frac{1}{2} (33) \\
\\
&=\frac{33}{2}
\end{align}
二次関数もOKです。分数はどちらにせよ計算しづらいですが・・・。
・ $~\displaystyle \int_{1}^{3} x^3-x^2+3x-2 dx~$ を求める。
①まずは普通に計算した場合
\begin{align}
&\displaystyle \int_{1}^{3} x^3-x^2+3x-2dx \\
\\
&=\left[ \frac{1}{4}x^4-\frac{1}{3}x^3+\frac{3}{2}x^2-2x \right]_{1}^{3} \\
\\
&=\frac{81}{4}-9+\frac{27}{2}-6-\frac{1}{4}+\frac{1}{3}-\frac{3}{2}+2\\
\\
&=\frac{58}{3}
\end{align}
②シンプソンの公式を使った場合
\begin{align}
f(1)&=1 \\
f(3)&=25 \\
\displaystyle f \left( \frac{1+3}{2} \right) &=f\left( 2 \right)=8
\end{align}
よって、
\begin{align}
&\displaystyle \int_{1}^{3} x^3-x^2+3x-2 dx \\
\\
&=\frac{3-1}{6} \left( 1+4\cdot 8+25 \right) \\
\\
&=\frac{1}{3} (58) \\
\\
&=\frac{58}{3}
\end{align}
シンプソンの公式を使うと、分数計算はほぼ皆無です。これは便利!!
Ⅲ 反例
次、 $~f(x)~$ の条件を満たさない関数について計算してみます。
・ $~\displaystyle \int_{0}^{2} 5x^4-2x^3+3x^2+x-3 dx~$ を求める。
①まずは普通に計算した場合
\begin{align}
&\displaystyle \int_{0}^{2} 5x^4-2x^3+3x^2+x-3dx \\
\\
&=\left[ x^5-\frac{1}{2}x^4+x^3+\frac{1}{2}x^2-3x \right]_{0}^{2} \\
\\
&=32-8+8+2-6\\
\\
&=28
\end{align}
②シンプソンの公式を使った場合
\begin{align}
f(0)&=-3 \\
f(2)&=75 \\
\displaystyle f \left( \frac{0+2}{2} \right) &=f\left( 1 \right)=4
\end{align}
よって、
\begin{align}
&\displaystyle \int_{0}^{2} 5x^4-2x^3+3x^2+x-3 dx \\
\\
&=\frac{2-0}{6} \left( -3+4\cdot 4+75 \right) \\
\\
&=\frac{1}{3} (88) \\
\\
&=\frac{88}{3}
\\
&\fallingdotseq 29.3
\end{align}
ある程度の近似はできるものの、4次になると答えが一致しなくなってしまいました。
・ $~\displaystyle \int_{0}^{2} e^x dx~$ を求める。
①まずは普通に計算した場合
\begin{align}
\displaystyle \int_{0}^{2} e^xdx &=\left[ e^x \right]_{0}^{2} \\
\\
&=e^2-1\\
\\
&\fallingdotseq 6.39
\end{align}
②シンプソンの公式を使った場合
\begin{align}
f(0)&=1 \\
f(2)&=e^2 \\
\displaystyle f \left( \frac{0+2}{2} \right) &=f\left( 1 \right)=e
\end{align}
よって、
\begin{align}
&\displaystyle \int_{0}^{2} e^x dx \\
\\
&=\frac{2-0}{6} \left( 1+4\cdot e+e^2 \right) \\
\\
&=\frac{1}{3}\left( e^2+4e+1 \right) \\
\\
&\fallingdotseq 6.42
\end{align}
指数関数についても、それなりの精度で近似できるものの、同じ値にはなりませんでした。
Ⅳ 証明1
本記事の証明では、3次以下の $~f(x)~$ において、シンプソンの公式が成り立つことを言います。
$~f(x)=Ax^3+Bx^2+Cx+D~$ とおく。
①左辺を計算していく
\begin{align}
&\displaystyle \int_{a}^{b} f(x)dx \\
\\
&=\left[ \frac{1}{4}Ax^4+\frac{1}{3}Bx^3+\frac{1}{2}Cx^2+Dx \right]_{a}^{b} \\
\\
&=\frac{1}{4}A(b-a)^4+\frac{1}{3}B(b-a)^3+\frac{1}{2}C(b-a)^2+D(b-a) \\
\\
&=\frac{1}{4}A(b^2-a^2)(b^2+a^2)+\frac{1}{3}B(b-a)(b^2+ba+a^2) \\
&+\frac{1}{2}C(b-a)(b+a)+D(b-a) \\
\\
&=\frac{1}{4}A(b-a)(b+a)(b^2+a^2)+\frac{1}{3}B(b-a)(b^2+ba+a^2) \\
&+\frac{1}{2}C(b-a)(b+a)+D(b-a) \\
\\
&=\frac{(b-a)}{6}\left\{ \frac{3}{2}A(b+a)(b^2+a^2)+2B(b^2+ba+a^2)+3C(b+a)+6D \right\}
\end{align}
\begin{align}
&\displaystyle \int_{a}^{b} f(x)dx \\
\\
&=\left[ \frac{1}{4}Ax^4+\frac{1}{3}Bx^3+\frac{1}{2}Cx^2+Dx \right]_{a}^{b} \\
\\
&=\frac{1}{4}A(b-a)^4+\frac{1}{3}B(b-a)^3 \\
&+\frac{1}{2}C(b-a)^2+D(b-a) \\
\\
&=\frac{1}{4}A(b^2-a^2)(b^2+a^2) \\
&+\frac{1}{3}B(b-a)(b^2+ba+a^2) \\
&+\frac{1}{2}C(b-a)(b+a)+D(b-a) \\
\\
&=\frac{1}{4}A(b-a)(b+a)(b^2+a^2) \\
&+\frac{1}{3}B(b-a)(b^2+ba+a^2) \\
&+\frac{1}{2}C(b-a)(b+a)+D(b-a) \\
\\
&=\frac{(b-a)}{6}\left\{ \frac{3}{2}A(b+a)(b^2+a^2) \right. \\
&\left. +2B(b^2+ba+a^2)+3C(b+a)+6D \right\}
\end{align}
②右辺を計算していく
まずは次の値を求める。
\begin{align}
f(a)&=Aa^3+Ba^2+Ca+D \\
f(b)&=Ab^3+Bb^2+Cb+D \\
\\
\displaystyle f\left( \frac{a+b}{2} \right) &= A \left( \frac{a+b}{2} \right)^3+B\left( \frac{a+b}{2} \right)^2+C\left( \frac{a+b}{2} \right)+D \\
\\
&=\frac{1}{4} \left\{ \frac{1}{2}A(a+b)^3+B(a+b)^2+2C(a+b)+4D \right\}
\end{align}
\begin{align}
f(a)&=Aa^3+Ba^2+Ca+D \\
f(b)&=Ab^3+Bb^2+Cb+D \\
\end{align}
\begin{align}
&\displaystyle f\left( \frac{a+b}{2} \right) \\
\\
&= A \left( \frac{a+b}{2} \right)^3+B\left( \frac{a+b}{2} \right)^2 \\
&+C\left( \frac{a+b}{2} \right)+D \\
\\
&=\frac{1}{4} \left\{ \frac{1}{2}A(a+b)^3+B(a+b)^2 \right. \\
&\left. +2C(a+b)+4D \right\}
\end{align}
これらを右辺の中かっこ内に代入する。
\begin{align}
&\displaystyle f(a)+4f\left( \frac{a+b}{2} \right) +f(b) \\
\\
&=Aa^3+Ba^2+Ca+D +\frac{1}{2}A(a+b)^3+B(a+b)^2+2C(a+b)+4D \\
&+Ab^3+Bb^2+Cb+D \\
\\
&=\frac{1}{2}A \left\{ 2a^3+(a+b)^3+2b^3 \right\} +B \left\{ a^2+(a+b)^2+b^2 \right\} \\
&+C\left\{ a+2(a+b)+b \right\} +6D \\
\\
&=\frac{1}{2}A ( 2a^3+a^3+3a^2b+3ab^2+b^3+2b^3 ) \\
&+B ( a^2+a^2+2ab+b^2+b^2 )+C( a+2a+2b+b ) +6D \\
\\
&=\frac{1}{2}A ( 3a^3+3a^2b+3ab^2+3b^3 )+B ( 2a^2+2ab+2b^2 )+C( 3a+3b ) +6D \\
\\
&=\frac{3}{2}A ( a^3+a^2b+ab^2+b^3 )+2B ( a^2+ab+b^2 )+3C( a+b ) +6D \\
\\
&=\frac{3}{2}A (b+a)(b^2+a^2)+2B ( b^2+ba+a^2 )+3C( b+a ) +6D \\
\end{align}
\begin{align}
&\displaystyle f(a)+4f\left( \frac{a+b}{2} \right) +f(b) \\
\\
&=Aa^3+Ba^2+Ca+D+\frac{1}{2}A(a+b)^3 \\
&+B(a+b)^2+2C(a+b)+4D \\
&+Ab^3+Bb^2+Cb+D \\
\\
&=\frac{1}{2}A \left\{ 2a^3+(a+b)^3+2b^3 \right\} \\
&+B \left\{ a^2+(a+b)^2+b^2 \right\} \\
&+C\left\{ a+2(a+b)+b \right\} +6D \\
\\
&=\frac{1}{2}A ( 3a^3+3a^2b+3ab^2+3b^3 ) \\
&+B ( 2a^2+2ab+2b^2 )+C( 3a+3b ) +6D \\
\\
&=\frac{3}{2}A ( a^3+a^2b+ab^2+b^3 ) \\
&+2B ( a^2+ab+b^2 )+3C( a+b ) +6D \\
\\
&=\frac{3}{2}A (b+a)(b^2+a^2) \\
&+2B ( b^2+ba+a^2 )+3C( b+a ) +6D \\
\end{align}
よって、
\begin{equation}
(右辺)=\displaystyle \frac{b-a}{6} \left\{ \frac{3}{2}A (b+a)(b^2+a^2)+2B ( b^2+ba+a^2 )+3C( b+a ) +6D \right\}
\end{equation}
\begin{align}
&(右辺) \\
&=\frac{(b-a)}{6}\left\{ \frac{3}{2}A(b+a)(b^2+a^2) \right. \\
&\left. +2B(b^2+ba+a^2)+3C(b+a)+6D \right\}
\end{align}
となるため、①より(左辺)=(右辺)である。
以上より、シンプソンの公式が示された。 $~\blacksquare~$
因数分解を駆使して、両辺を同じ形に揃えていくタイプの証明方法でした。
次回はもう少し高度な視点からシンプソンの公式を見てみようと思います!!

◇参考文献等
・高木貞治(2012)『定本 解析概論』,pp.136-137,岩波書店.
・「高校数学.net」,<http://xn--48s96ub7b0z5f.net/simpson/> 2018年7月25日アクセス
・「記号の世界ゟ」,<http://tetobourbaki.hatenablog.com/entry/2017/05/06/172340> 2018年7月25日アクセス
![[商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。] [商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。]](https://hbb.afl.rakuten.co.jp/hgb/16fb715f.fc69e075.16fb7160.6ce178fe/?me_id=1213310&item_id=13934101&m=https%3A%2F%2Fthumbnail.image.rakuten.co.jp%2F%400_mall%2Fbook%2Fcabinet%2F2092%2F9784000052092.jpg%3F_ex%3D80x80&pc=https%3A%2F%2Fthumbnail.image.rakuten.co.jp%2F%400_mall%2Fbook%2Fcabinet%2F2092%2F9784000052092.jpg%3F_ex%3D128x128&s=128x128&t=picttext)
定本解析概論 [ 高木貞治 ]
|
コメント
コメント一覧 (10件)
先生、おはようございます!!
TwitterでDMをお送りしようと思ったのですが、フォローしていただかないと送れないようでした_| ̄|○
すず、という名でフォローしております!
よろしくお願いいたします!!
すみません。DMの設定変えました!!
先生!
わかりやすい図を添付してくださり、本当にありがとうございます!!
画像を添付したいのですが、こちらでは出来ないようですのでTwitterのアカウントをつくってお送りしてもよろしいでしょうか。
いつも本当にありがとうございます!
画像アップできないのは知りませんでした。
サイト、少しいじってみます。
Twitterお待ちしております。
先生、お忙しいところありがとうございます!
もしよろしければ図があるととても助かります・・
偶数奇数で頭がこんがらがってしまい・・
すみません_| ̄|○
まず、\(~\displaystyle \int_{0}^{\pi} \sin^n{\theta}~d\theta ~\)についてですが、下の図を見ればわかる通り、0から\(~\displaystyle \frac{\pi}{2}~\)と、\(~\displaystyle \frac{\pi}{2}~\)から\(~\pi~\)において、\(~\sin{\theta}~\)はどちらも+です。
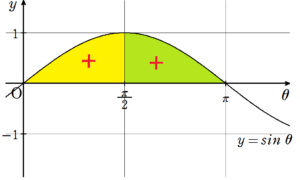
よって、
\begin{equation}
\displaystyle \int_{0}^{\frac{\pi}{2}} \sin^n{\theta}~d\theta=\int_{\frac{\pi}{2}}^{\pi} \sin^n{\theta}~d\theta
\end{equation}
が成り立つので、
\begin{align}
~\displaystyle \int_{0}^{\pi} \sin^n{\theta}~d\theta \\
\\
&=\int_{0}^{\frac{\pi}{2}} \sin^n{\theta}~d\theta=\int_{\frac{\pi}{2}}^{\pi} \sin^n{\theta}~d\theta \\
\\
&=\int_{0}^{\frac{\pi}{2}} \sin^n{\theta}~d\theta+\int_{0}^{\frac{\pi}{2}} \sin^n{\theta}~d\theta \\
\\
&=2\displaystyle \int_{0}^{\frac{\pi}{2}} \sin^n{\theta}~d\theta
\end{align}
となります。
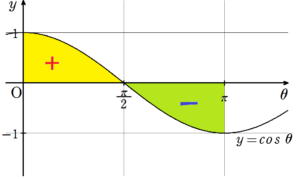
同様の考え方で、\(~\cos{\theta}~\)の正負は下の図のようになります。
よって、\(~n~\)が奇数なら、負の面積になりますので、
\begin{equation}
\displaystyle \int_{0}^{\frac{\pi}{2}} \cos^n{\theta}~d\theta=-\int_{\frac{\pi}{2}}^{\pi} \cos^n{\theta}~d\theta
\end{equation}
が成り立ち、\(~n~\)が偶数なら、正に戻りますので、
\begin{equation}
\displaystyle \int_{0}^{\frac{\pi}{2}} \cos^n{\theta}~d\theta=\int_{\frac{\pi}{2}}^{\pi} \cos^n{\theta}~d\theta
\end{equation}
となります。
あとは、\(~\displaystyle \int_{0}^{\pi} \sin^n{\theta}~d\theta ~\)の時と同じように考えてあげればOKです。
先生、おはようございます!早速のご解説ありがとうございます!
応用編も楽しみにしております♪───O(≧∇≦)O────♪
P・S
ウォリス積分なのですが、
積分区間が0からπ/2だけでなく、
0~π、0~2π、-π/2~π/2など・・でも図を描いて簡単に何倍かすることで使えるみたいなのですが、この部分をもしよろしければ取り上げていただけませんでしょうか><
よろしくお願いいたします!今日も暑くなりそうですので、くれぐれも御自愛ください!
応用編はまた木曜日に作るつもりです!!
ウォリス積分の件ですが、注目すべきは\(~\sin{\theta}~,~\cos{\theta}~\)の符号です。
例えば、
\(~\displaystyle \int_{0}^{\pi} \sin^n{\theta}~d\theta ~\)であれば、
0から\(~\displaystyle \frac{\pi}{2}~\)と、\(~\displaystyle \frac{\pi}{2}~\)から\(~\pi~\)における\(~\sin{\theta}~\)の積分は同じなので、
\(~\displaystyle \int_{0}^{\pi} \sin^n{\theta}~d\theta=2\displaystyle \int_{0}^{\frac{\pi}{2}} \sin^n{\theta}~d\theta ~\)
です。
ただ、\(~\displaystyle \int_{0}^{\pi} \cos^n{\theta}~d\theta ~\)なら、
0から\(~\displaystyle \frac{\pi}{2}~\)と、\(~\displaystyle \frac{\pi}{2}~\)から\(~\pi~\)における\(~\cos{\theta}~\)の積分は逆符号になるので、
指数が奇数か偶数かで場合分けが必要です。
\(~n~\)が奇数のときは、
\begin{align}
&~~~\displaystyle \int_{0}^{\pi} \cos^n{\theta}~d\theta \\
\\
&=\displaystyle \int_{0}^{\frac{\pi}{2}} \cos^n{\theta}~d\theta + \int_{\frac{\pi}{2}}^{\pi} \cos^n{\theta}~d\theta \\
\\
&=\displaystyle \int_{0}^{\frac{\pi}{2}} \cos^n{\theta}~d\theta ~ – \displaystyle \int_{0}^{\frac{\pi}{2}} \cos^n{\theta}~d\theta
\\
\\
&=0
\end{align}
\(~n~\)が偶数のときは、
\begin{align}
&~~~\displaystyle \int_{0}^{\pi} \cos^n{\theta}~d\theta \\
\\
&=\displaystyle \int_{0}^{\frac{\pi}{2}} \cos^n{\theta}~d\theta + \int_{\frac{\pi}{2}}^{\pi} \cos^n{\theta}~d\theta \\
\\
&=\displaystyle \int_{0}^{\frac{\pi}{2}} \cos^n{\theta}~d\theta + \displaystyle \int_{0}^{\frac{\pi}{2}} \cos^n{\theta}~d\theta
\\
&=2 \int_{0}^{\frac{\pi}{2}} \cos^n{\theta}~d\theta
\end{align}
となります。
この考え方により、積分範囲が\(~\displaystyle \frac{\pi}{2}~\)刻みならウォリス積分へと帰着させることができます。
先生!
リクエストにお応えくださり、本当にありがとうございます!!(感涙)
シンプソンの公式、ものすごーーく不思議な気持ちになりますね!
端っこと積分区間の真ん中の面積さえもとまれば体積でも求められるということですよね・・
先生! 3次式ということは、logxやe^xや三角関数はどのような扱いになるのでしょうか・・
マクローリン展開で近似しますと3次以上になってしまうので、シンプソンは使えない・・ということでしょうか><
いつもありがとうございます!
すずさん
こんにちは。
いろいろと計算して確かめていく度に不思議だなぁ~と思って記事を作っていました!
面積に関しても同様に求められそうです。(まだ試していません)
\(~\log{x}~\)や\(~e^x~\)に関しても、ご指摘の通りです。
すべての自然数\(~n \le 4 ~\)において、\(~n~\)階微分が\(~0~\)の場合にのみ、シンプソンの公式が成り立ちます。
\(~n~\)次導関数が\(~0~\)でなくても、ある程度の近似はできますが・・・。
夏休み中にもっとシンプソンの公式への理解をもっと深めようと思います。