
縦・横・斜めの数の和がすべて等しくなるように数が配置される魔方陣。
この記事では、3×3の魔方陣の論理的な作り方を解説します。
- 魔方陣とは何か
- 魔方陣を論理的に作るにはどうすればよいか
Ⅰ 魔方陣とは
「まほうじん」と聞くと、ゲーム等で出てくる「魔法陣」を思い浮かべる方もいますが、数学の「まほうじん」は魔法の四角形という意味合いで「魔方陣」と書きます。
英語にすると“magic square “ です。まずは、この魔方陣の定義を確認しておきましょう。
$~n\times n~$ の魔方陣とは、 $~1~,~2~,~\cdots~,~n^2~$ の自然数を $~n\times n~$ の正方形のマスに入れ、縦・横・斜めの数の和が一定になるものを言う。
今回考える3×3の魔方陣で言えば、 $~1,2,3,4,5,6,7,8,9~$を各マスに入れ、 縦・横・斜めの和が等しくなるようにしなければなりません。
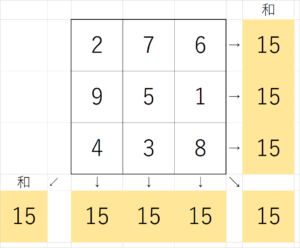
<図1>のように、3×3の魔方陣では縦・横・斜めで合計8ラインあります。
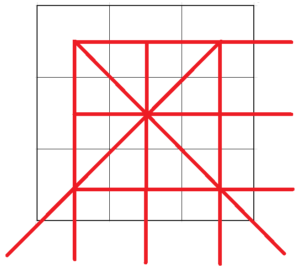

では、3×3の魔法陣の論理的な作り方を次章で解説しましょう。
Ⅱ 3×3魔方陣の作り方
以下の手順で3×3の魔方陣を一意的に作ることができます。
- 1ラインの和を求める
- 中央の数を求める
- 1の場所を求める
- 1の周りを埋める
- 全マス埋める
では、各手順について細かく見てみましょう。
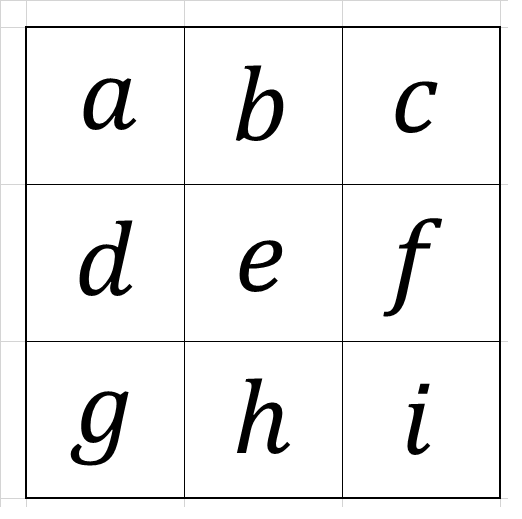
下のような魔方陣で考える。
ただし、$~a~$ ~ $~i~$ にはそれぞれ1~9の自然数が1つずつ入るものとする。
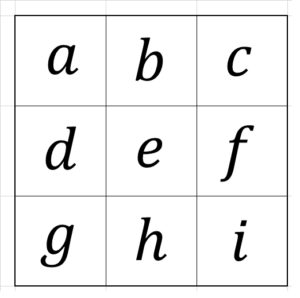

このとき、次の式が成り立つ。
\begin{align*}
&a+b+c+d+e+f+g+h+i \\
&=1+2+3+4+5+6+7+8+9 \\
&=45 ~~~~\cdots ①
\end{align*}$①$より、
\begin{equation*}
(a+b+c)+(d+e+f)+(g+h+i)=45
\end{equation*}となるため、それぞれのカッコ内の式が各行の和$~S~$を表すことから、
\begin{align*}
S+S+S&=45 \\
3S&=45 \\
S&=15
\end{align*}が求まった。
次に、中央の数を通る4ラインの和について考えると、次の等式が成り立つ。
\begin{equation*}
(a+e+i)+(b+e+h)+(c+e+g)+(d+e+f)=15 \times 4
\end{equation*}項のまとまりを変えることで、
\begin{equation*}
(a+b+c+d+e+f+g+h+i)+3e=60
\end{equation*}
であり、$①$より、
\begin{align*}
45+3e&=60 \\
3e&=15 \\
e&=5
\end{align*}と、中央の数$~e~$が求まった。
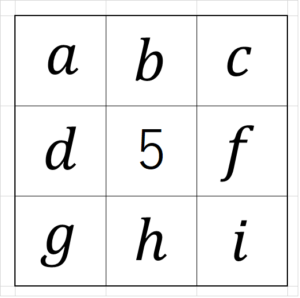

3つの数のうちの1つが$~1~$であるとすると、残りの2つの数で和が15になるようにするためには、
- $~1~,~5~,9~$の組み合わせ
- $~1~,~6~,8~$の組み合わせ
の2パターンしかない。
そのため、四隅である( $~a~,~c~,~g~,~i~$ )は縦・横・斜めの3ラインに影響するため、$~1~$を配置することができない。
すなわち、1は $~b~,~d~,~f~,~h~$ のどこかに配置される。
魔方陣は左右・上下対称なので、 $~b~,~d~,~f~,~h~$ のどこに置いても一般性は失われない。
そこで、今回は $~b=1~$ とする。
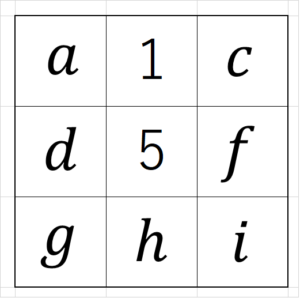

STEP3より、$~1~$と同じライン上には、$~5~$と $~9~$ の組み合わせか $~6~$ と $~8~$ の組み合わせしかないため、 $~h=9~$ がわかる。
さらに、 $~a~,~c~$ には $~6~$ と $~8~$ が入ることがわかりますが、魔方陣は左右対称であることから、 $~a~,~c~$ どちらを $~6~$ にしても一般性は失われない。
そこで、今回は $~a=6~,~c=8~$ とする。
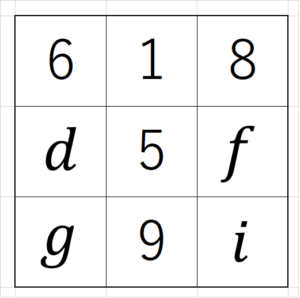

ここまでくればあとは自然に埋まります。斜めに注目すれば、
\begin{align*}
8+5+g&=15 \\
g&=2 \\
\\
6+5+i&=15 \\
i&=4
\end{align*}が求まる。
また、1列目、3列目に注目すれば、
\begin{align*}
6+d+2&=15 \\
d&=7\\
\\
8+f+4&=15 \\
f&=3
\end{align*}が求まるため、魔方陣が完成した。
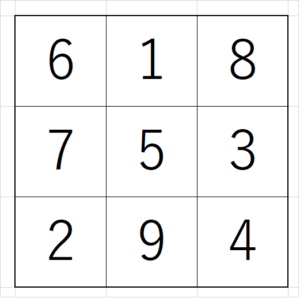

「一般性は失われない」という難しい日本語を使いましたが、要は「何を入れても結果的には一緒ですよ~」という意味です。
以上、数をあてはめて試行錯誤するのではなく、論理的に魔方陣を完成させる方法でした!
他にも魔方陣に関する記事を書いているので、是非ご覧ください↓↓




さらには、こんな魔方陣まで!!↓↓





パズルとして楽しめなくなっちゃったにゃ。



ま、まぁね。
でも、数学得意の数式や背理法を使えば、パズルも機械的に解くことができることが証明されたよ。



コメント