魔方陣よりもレア？ 3×3×3の立方陣の定義と例を紹介！

　平面における$~3\times 3~$の魔方陣は多くの人に知られていますが、その立体バージョンである立方陣はご存知でしょうか。

　魔方陣と同様、縦と横の3つの数の和が等しくなるだけでなく、上下の3つの数の和まで等しくなるという奇跡のような図形です。

　この記事では、立方陣の定義を解説すると共に、その条件を満たした中で最も美しい立方陣を紹介します！

立方陣とは？

　まず、平面の$~3\times 3~$の魔方陣は、次のようなものでした。（「３×３の魔方陣の作り方」より）

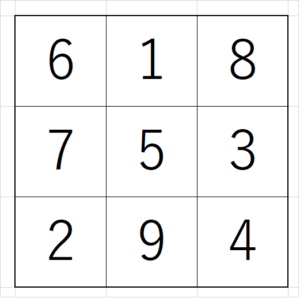
　$~3\times 3~$の魔方陣の定義は、「１～９の自然数を、３×３の正方形のマスに１つずつ入れ、縦・横・斜めの数の和が一定になる」というものでした。

立方陣の定義は縦・横・上下の和が一定

　今回考える$~3\times 3 \times 3~$の立体の魔方陣、つまり立方陣の定義は次のように行います。

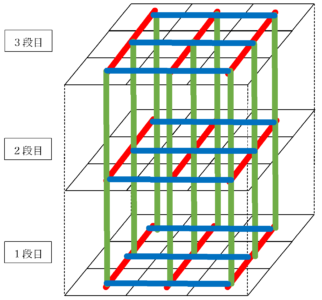
　魔方陣と同様に考えてしまうと、立体の中心を通る対角線や、1つの面の中の対角線などの全てのラインの和が一定にならなければいけません。

　しかし、$~3\times 3\times 3~$の場合はそのような数字の組み合わせはありません。

　そのため、この記事における立方陣は、縦・横・上下の計27ラインの和が一定となるようなものを考えていきます。

立方陣の1ラインの和は42

　立方陣に数字を埋めていく前に、１ラインの和がいくつになるのかを求めておきます。
 
　使う数字である$~1~$から$~27~$までの自然数の和は、

 \frac{27 \times 28}{2}=378

　図3のように、縦ラインだけに注目すると、1段につき3ライン。
　全体で9ラインあるので、$~378 \div 9=42~$。

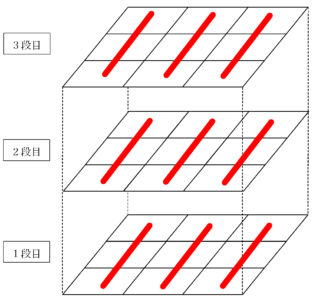
　すなわち、1ラインの和は$~42~$と求まりました。
 
　この記事では、これ以上は数学的に求めません。 （３×３の魔方陣とは比較にならないほど複雑なので・・・）
 
　いろいろな$~3\times 3 \times 3~$の立方陣を、次の章でお示しします。 （作り方はうまくまとめられたら記事にしようと思っています・・・）

立方陣の例

　何個か立方陣を作ってみました。
　縦・横・上下以外で、1ラインの和が$~42~$となっているところを探してみましょう。

例1：縦横上下以外に5ライン

　まず1つ目の立方陣はこちら。

 立方陣の例1

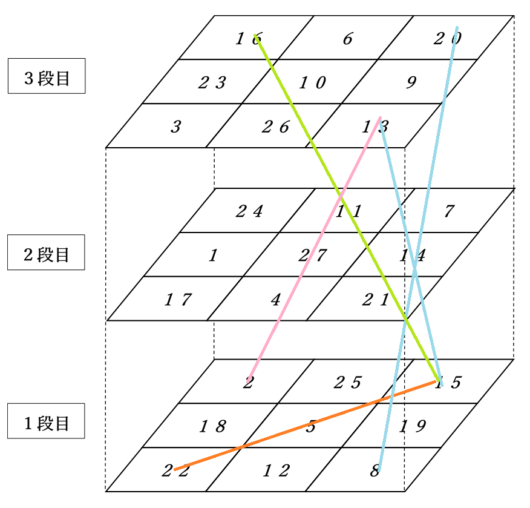
　この立方陣は、縦・横・上下以外に、和が$~42~$となっているのが5ラインあります。

　見づらいので、数式も書いておきます。

$~22+5+15=42~$
$~16+11+15=42~$
$~13+14+15=42~$
$~20+14+8=42~$
$~13+27+2=42~$

  　2段目の真ん中が$~27~$というのが、アンバランスですよね。

例2：縦横上下以外に7ライン

　2つ目は、和が$~42~$のラインをさらに増やせるよう、配置を変えてみました。

 立方陣の例2

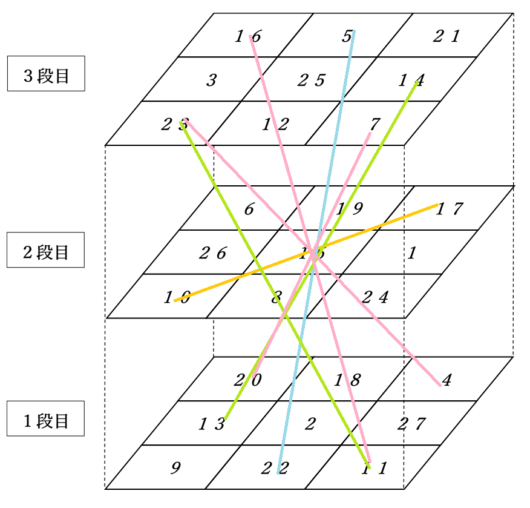
　今回の立方陣は、縦・横・上下以外に、和が$~42~$となっているのが7ラインあります。

　先ほどよりもさらに見づらいので、数式で指しているところを確かめてみましょう。

$~17+15+10=42~$
$~14+15+13=42~$
$~23+8+11=42~$
$~5+15+22=42~$
$~16+15+11=42~$
$~23+15+4=42~$
$~7+15+20=42~$

　立方体の対角線が4ライン中3ライン揃っているのがすごいですね。

例3：縦横上下以外に10ライン

　これが最も美しい立方陣です！

 立方陣の例3

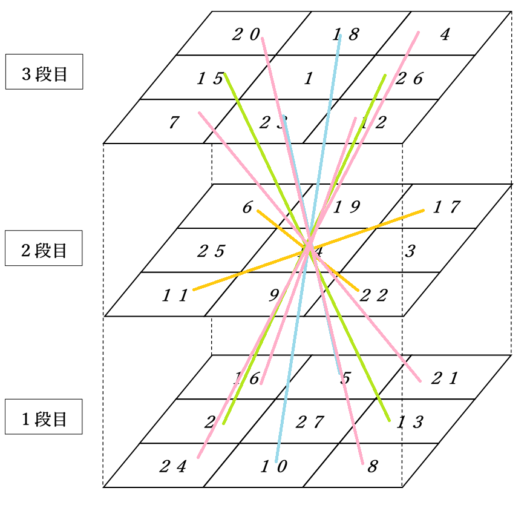
　図6の立方陣は、縦・横・上下以外に、和が$~42~$となっているのが１０ラインあります。

$~6+14+22=42~$
$~17+14+11=42~$
$~15+14+13=42~$
$~26+14+2=42~$
$~18+14+10=42~$
$~23+14+5=42~$
$~20+14+8=42~$
$~4+14+24=42~$
$~7+14+21=42~$
$~12+14+16=42~$

　すべて中央の$~14~$を通っていて、ラインが対称形。
　これが$~3\times 3 \times 3~$の立方陣の最も美しい形です。
 

まとめ：すべてのラインの和が等しくはならない

　魔方陣は縦・横・斜めのすべての和が等しくなるように作ることができました。

　立方陣に関しては、縦・横・上下に加えて10ラインが限界です。

　魔方陣でもそうですが、登場する自然数の中央値である$~14~$をど真ん中に入れることで、最も美しい立方陣が作れます。

　その美しさをいろいろな人と共有してもらえると嬉しいです！

縦・横・上下が揃っている時点ですごいにゃ。

計算はExcelで行ってしまいました。手計算だと確かめるのが大変‥‥。