★魔方陣の関連記事はこちら↓★
・「3×3の魔方陣の作り方」
・「3×3魔方陣のもつ性質」
・「積の魔方陣」
・「3×3×3の立方陣」(立体バージョンの魔方陣)
Ⅰ すごい性質
以前の記事「3×3の魔方陣の作り方」で紹介したように、3×3の魔方陣は次のように定まりました。
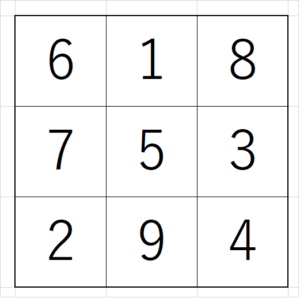
この魔方陣に隠された性質を2つほど「3×3魔方陣のもつ性質」で紹介しましたが、今回はさらにすごい性質について紹介します。
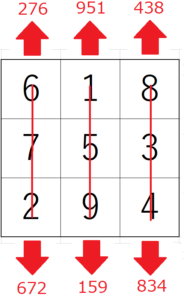
3×3の魔方陣において、次の2つの計算式が成り立つ。
\begin{equation}
672^2+159^2+834^2=276^2+951^2+438^2
\end{equation}
\begin{align}
&672^2+159^2+834^2 \\
&=276^2+951^2+438^2
\end{align}
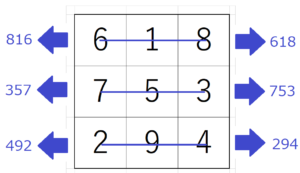
\begin{equation}
618^2+753^2+294^2=816^2+357^2+492^2
\end{equation}
\begin{align}
&618^2+753^2+294^2 \\
&=816^2+357^2+492^2
\end{align}
一言では表しにくいので、性質名はつけません。そして、この性質を口で説明するのにはちょっと余白が足りない(笑)
とにかく奇跡と呼べるような性質です。
実際に計算して確かめてみましょう。
\begin{align}
672^2&=451584 \\
159^2&=25281 \\
834^2&=695556 \\
276^2&=76176 \\
951^2&=904401 \\
438^2&=191844 \\
\end{align}
以上より、
\begin{align}
672^2+159^2+834^2&=1172421 \\
816^2+357^2+492^2&=1172421
\end{align}
\begin{align}
618^2&=381924 \\
753^2&=567009 \\
294^2&=86436 \\
816^2&=665856 \\
357^2&=127449 \\
492^2&=242064 \\
\end{align}
以上より、
\begin{align}
618^2+753^2+294^2&=1035369 \\
816^2+357^2+492^2&=1035369
\end{align}
よって題意は示された。 $~\blacksquare$
計算結果がどちらも素数・・・ではありませんでした。当然ながら3の倍数です。魔方陣をどう組んだとしても、この2パターンの計算式しか挙がらないので、証明はこれで一応完了です。
Ⅱ 証明
計算量がすごいことになりますが、文字式での証明もしてみました。
縦の計算式(赤い数式)について、証明をする。
3×3の魔方陣の各マスを、下図のように $~a~$ ~ $~i~$ とおく。
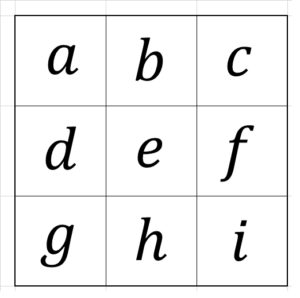
\begin{align}
&(100a+10d+g)^2+(100b+10e+h)^2+(100c+10f+i)^2 \\
&=(100g+10d+a)^2+(100h+10e+b)^2+(100i+10f+c)^2
\end{align}
を証明したいので、左辺と右辺それぞれを展開していく。
左辺をまず展開すると、
\begin{align}
&(100a+10d+g)^2+(100b+10e+h)^2+(100c+10f+i)^2 \\
\\
&=10000a^2+100d^2+g^2+2000ad+20dg+200ag+10000b^2+100e^2+h^2 \\
&+2000be+20eh+200bh+10000c^2+100f^2+i^2+2000cf+20fi+200ci \\
\end{align}
同様に右辺も展開すると、
\begin{align}
&(100g+10d+a)^2+(100h+10e+b)^2+(100i+10f+c)^2 \\
\\
&=10000g^2+100d^2+a^2+2000dg+20ad+200ag+10000h^2+100e^2+b^2 \\
&+2000eh+20be+200bh+10000i^2+100f^2+c^2+2000fi+20cf+200ci \\
\end{align}
(左辺)-(右辺)より、
\begin{align}
&10000(a^2+b^2+c^2-g^2-h^2-i^2)-(a^2+b^2+c^2-g^2-h^2-i^2) \\
&+2000(ad+be+cf-dg-eh-fi)-20(ad+be+cf-dg-eh-fi) \\
\\
&=9999(a^2+b^2+c^2-g^2-h^2-i^2)+1980(ad+be+cf-dg-eh-fi) \\
\end{align}
ここで、次の2つの補題を利用する。
\begin{align}
&(100a+10d+g)^2+(100b+10e+h)^2 \\
&+(100c+10f+i)^2 \\
\\
&=(100g+10d+a)^2+(100h+10e+b)^2 \\
&+(100i+10f+c)^2
\end{align}
を証明したいので、左辺と右辺それぞれを展開していく。
左辺をまず展開すると、
\begin{align}
&(100a+10d+g)^2+(100b+10e+h)^2 \\
&+(100c+10f+i)^2 \\
\\
&=10000a^2+100d^2+g^2+2000ad \\
&+20dg+200ag+10000b^2+100e^2 \\
&+h^2+2000be+20eh+200bh \\
&+10000c^2+100f^2+i^2 \\
&+200cf+20fi+200ci \\
\end{align}
同様に右辺も展開すると、
\begin{align}
&(100g+10d+a)^2+(100h+10e+b)^2 \\
&+(100i+10f+c)^2 \\
\\
&=10000g^2+100d^2+a^2+2000dg \\
&+20ad+200ag+10000h^2+100e^2 \\
&+b^2+2000eh+20be+200bh \\
&+10000i^2+100f^2+c^2 \\
&+2000fi+20cf+200ci \\
\end{align}
(左辺)-(右辺)より、
\begin{align}
&10000(a^2+b^2+c^2-g^2-h^2-i^2) \\
&-(a^2+b^2+c^2-g^2-h^2-i^2) \\
&+2000(ad+be+cf-dg-eh-fi) \\
&-20(ad+be+cf-dg-eh-fi) \\
\\
&=9999(a^2+b^2+c^2-g^2-h^2-i^2) \\
&+1980(ad+be+cf-dg-eh-fi) \\
\end{align}
ここで、次の2つの補題を利用する。
3×3魔方陣で次の式が成り立つ。
\begin{equation}
a^2+d^2+g^2=c^2+f^2+i^2
\end{equation}
証明
「3×3魔方陣のもつ性質/Ⅰ 両端平方和の法則」の証明を参照。
3×3魔方陣で次の式が成り立つ。
\begin{equation}
ad+be+cf=dg+eh+fi
\end{equation}
証明
「3×3魔方陣のもつ性質/Ⅱ 中央積和の法則」の証明を参照。
これにより、次の2つの式が言える。
\begin{align}
a^2+d^2+g^2&=c^2+f^2+i^2 \\
ad+be+cf&=dg+eh+fi
\end{align}
よって、
\begin{align}
&(左辺)-(右辺) \\
&=9999(a^2+b^2+c^2-g^2-h^2-i^2)+1980(ad+be+cf-dg-eh-fi) \\
&=9999 \cdot 0+1980 \cdot 0 \\
&=0
\end{align}
\begin{align}
&(左辺)-(右辺) \\
\\
&=9999(a^2+b^2+c^2-g^2-h^2-i^2) \\
&+1980(ad+be+cf-dg-eh-fi) \\
\\
&=9999 \cdot 0+1980 \cdot 0 \\
\\
&=0
\end{align}
したがって、(左辺)=(右辺)が言えた。 $~\blacksquare$
なかなか計算が大変でした・・・。
実は、このすごい法則の証明を考えている中で、 $~a^2+d^2+g^2=c^2+f^2+i^2~$ や $~ad+be+cf=dg+eh+fi~$ が成り立つことが予想され、先週書いたように証明しました。数学の楽しさを再認識させられる3週間でした。


コメント