今回は3×3魔方陣に隠された面白い性質について紹介します。
Ⅰ 両端平方和の法則
Ⅱ 中央積和の法則
★魔方陣の関連記事はこちら↓★
・「3×3の魔方陣の作り方」
・「3×3魔方陣のすごい性質」
・「積の魔方陣」
・「3×3×3の立方陣」(立体バージョンの魔方陣)
Ⅰ 両端平方和の法則
以前の記事「3×3の魔方陣の作り方」で紹介したように、3×3の魔方陣は次のように定まりました。
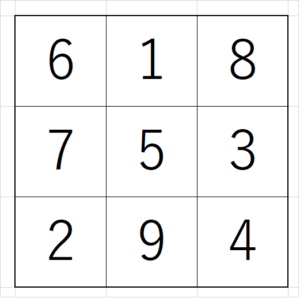
実は、この魔方陣には様々な数の「魔法」が隠れています。その中の1つが次の法則。
3×3の魔方陣において、次の計算式が成り立つ。
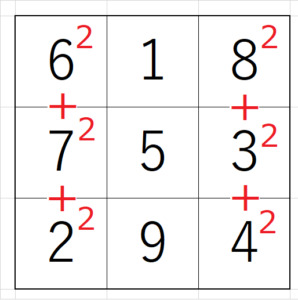
\begin{equation}
6^2+7^2+2^2=8^2+3^2+4^2
\end{equation}
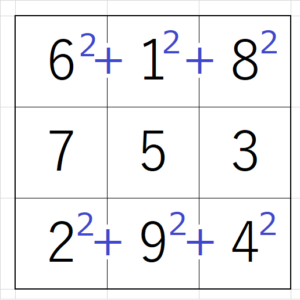
\begin{equation}
6^2+1^2+8^2=2^2+9^2+4^2
\end{equation}
これを勝手に「両端平方和の法則」と名付けておきます。
証明は簡単。単に計算をしてみればよいのです。
\begin{align}
6^2+7^2+2^2&=36+49+4 \\
&=89
\end{align}
\begin{align}
8^2+3^2+4^2&=64+9+16 \\
&=89
\end{align}
以上より、
\begin{equation}
6^2+7^2+2^2=8^2+3^2+4^2
\end{equation}
また、
\begin{align}
6^2+1^2+8^2&=36+1+64 \\
&=101
\end{align}
\begin{align}
2^2+9^2+4^2&=4+81+16 \\
&=101
\end{align}
以上より、
\begin{equation}
6^2+1^2+8^2=2^2+9^2+4^2
\end{equation}
題意は示された。 $~\blacksquare $
計算結果がどちらも素数というのがまた魅力的ですね。魔方陣をどう組んだとしても、この2パターンの計算式しか挙がらないので、証明はこれで完了ですが、一応文字式を使った証明方法も考えられます。
縦の計算式(赤い数式)について、証明をする。
3×3の魔方陣の各マスを、下図のように $~a~$ ~ $~i~$ とおく。
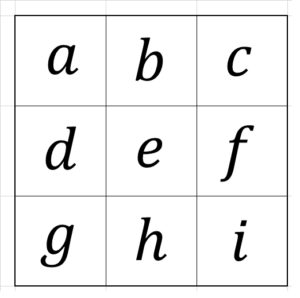
\begin{equation}
a^2+d^2+g^2=c^2+f^2+i^2
\end{equation}
を証明したいので、 $~a^2+d^2+g^2-(c^2+f^2+i^2)~$ を考える。
「3×3の魔方陣の作り方のⅡの①②」より、各ラインの和が15であり、 $~e=5~$ と求まっているため、次の式が成り立つ。
\begin{equation}
c=10-a,f=10-d,i=10-g
\end{equation}
これにより、
\begin{align}
&a^2+d^2+g^2-(c^2+f^2+i^2) \\
&=a^2+d^2+g^2-(10-a)^2-(10-d)^2-(10-g)^2 \\
&=a^2+d^2+g^2-(100-20a+a^2)-(100-20d+d^2)-(100-20g+g^2) \\
&=a^2+d^2+g^2-100+20a-a^2-100+20d-d^2-100+20g-g^2 \\
&=-100+20a-100+20d-100+20g \\
&=20(a+d+g)-300 \\
\end{align}
\begin{align}
&a^2+d^2+g^2-(c^2+f^2+i^2) \\
&=a^2+d^2+g^2-(10-a)^2 \\
&-(10-d)^2-(10-g)^2 \\
&=a^2+d^2+g^2-(100-20a+a^2) \\
&-(100-20d+d^2)-(100-20g+g^2) \\
&=a^2+d^2+g^2-100+20a-a^2 \\
&-100+20d-d^2-100+20g-g^2 \\
&=-100+20a-100+20d-100+20g \\
&=20(a+d+g)-300 \\
\end{align}
ここで、 $~a+d+g~$ は縦1列の和なので、 $~a+d+g=15~$ 。よって、
\begin{align}
(与式)&=20 \cdot 15-300 \\
&=0
\end{align}
以上より、
\begin{equation}
a^2+d^2+g^2-(c^2+f^2+i^2)=0 \\
a^2+d^2+g^2=c^2+f^2+i^2
\end{equation}
縦の計算式は示された。横の計算式(青い数式)も同様に示すことができる。 $~\blacksquare$
普通に計算して証明したほうが明らかに早そうですね・・・(><)
Ⅱ 中央積和の法則
これまた勝手に名付けた法則第2弾です。
3×3の魔方陣において、次の計算式が成り立つ。
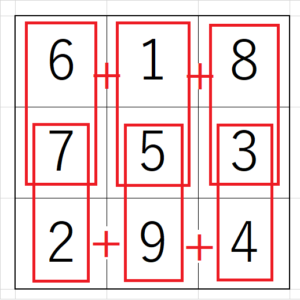
\begin{equation}
6×7+1×5+8×3=7×2+5×9+3×4
\end{equation}
\begin{align}
&6×7+1×5+8×3 \\
&=7×2+5×9+3×4
\end{align}
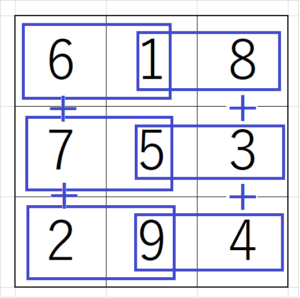
\begin{equation}
6×1+7×5+2×9=1×8+5×3+9×4
\end{equation}
\begin{align}
&6×1+7×5+2×9 \\
&=1×8+5×3+9×4
\end{align}
中央の行(列)を仲介にして、積の和が等しいことから「中央積和の法則」と名付けています。こちらについても、検算による証明と、文字式による証明をしておきましょう。
\begin{align}
6×7+1×5+8×3&=42+5+24 \\
&=71
\end{align}
\begin{align}
7×2+5×9+3×4&=14+45+12 \\
&=71
\end{align}
以上より、
\begin{equation}
6×7+1×5+8×3=7×2+5×9+3×4
\end{equation}
\begin{align}
&6×7+1×5+8×3 \\
&=7×2+5×9+3×4
\end{align}
また、
\begin{align}
6×1+7×5+2×9&=6+35+18 \\
&=59
\end{align}
\begin{align}
1×8+5×3+9×4&=8+15+36 \\
&=59
\end{align}
以上より、
\begin{equation}
6×1+7×5+2×9=1×8+5×3+9×4
\end{equation}
\begin{align}
&6×1+7×5+2×9 \\
&=1×8+5×3+9×4
\end{align}
題意は示された。 $~\blacksquare $
これまたそれぞれの和が素数というのが魅力的ですね。続いて文字式による証明。
縦の計算式(赤い数式)について、証明をする。
3×3の魔方陣の各マスを、下図のように $~a~$ ~ $~i~$ とおく。

\begin{equation}
ad+be+cf=dg+eh+fi
\end{equation}
を証明したいので、 $~ad+be+cf-(dg+eh+fi)~$ を考える。
「3×3の魔方陣の作り方のⅡの①②」より、各ラインの和が15であり、 $~e=5~$ と求まっているため、次の式が成り立つ。
\begin{equation}
g=10-c,h=10-b,i=10-a
\end{equation}
これにより、
\begin{align}
&ad+be+cf-(dg+eh+fi) \\
&=ad+be+cf-d(10-c)-e(10-b)-f(10-a) \\
&=ad+be+cf-10d+cd-10e+be-10f+af \\
&=(a+c)d+(a+c)f+2be-10(d+e+f) \\
&=(a+c)(d+f)+2be-10(d+e+f) \\
\end{align}
\begin{align}
&ad+be+cf-(dg+eh+fi) \\
&=ad+be+cf-d(10-c) \\
&-e(10-b)-f(10-a) \\
&=ad+be+cf-10d+cd \\
&-10e+be-10f+af \\
&=(a+c)d+(a+c)f+2be \\
&-10(d+e+f) \\
&=(a+c)(d+f)+2be-10(d+e+f) \\
\end{align}
であり、ここで、以下の4式を代入する。
\begin{cases}
a+c = 15-b &\\
d+f = 10 &\\
e=10 &\\
d+e+f=15 &\\
\end{cases}
すると、
\begin{align}
(与式)&=(15-b)\cdot 10 +2b \cdot 5-10\cdot 15 \\
&=150-10b+10b-150 \\
&=0
\end{align}
となる。以上より、
\begin{equation}
ad+be+cf-(dg+eh+fi)=0 \\
ad+be+cf=dg+eh+fi
\end{equation}
縦の計算式は示された。横の計算式(青い数式)も同様に示すことができる。 $~\blacksquare$
これまた、検算による証明のほうが早そうです・・・(><)(><)
今回は魔方陣を研究している中で見えてきた2つの法則について、勝手に名付け、証明を与えました。
魔方陣の研究、楽しい(^^)


コメント
コメント一覧 (2件)
(A-C)+(G-I)=F-D
A+C+G+I-E=B+D+F+H-E=3E
コメントありがとうございます。上式も美しいですね。
\(~a+g=15-d~,~c+i=15-f~\)を使えば\(~(a+c)+(g-i)=f-d~\)が、\(~a+i=10~,~c+g=10~\)を使えば\(~a+c+g+i-e=3e~\)が示せそうです。