中３修了– tax –

10世紀の科学者アルハゼン（イブン・アル・ハイサム）によって発見された「アルハゼンの定理」について、幾何学的な観点から分かりやすく解説しています。 この定理は中学3年生で習う「円周角の定理」の応用にあたりますが、実は簡単に証明をすることができます。この記事では、アルハゼンの定理の使い方や2種類の証明方法について、数学史を交えながら解説しています。

9世紀のイスラム科学の黄金期に活躍した学者、サービト・イブン・クッラの生涯と業績に迫ります。数学における「友愛数」の公式の発見者として知られるだけでなく、フワーリズミーの二次方程式の研究を一般化したことでも有名です。また、翻訳家として活躍したことも数学史に大きな影響を与えました。

9世紀にアッバース朝で活躍した数学者アル・フワーリズミーの功績とその影響について詳しく解説しています。「代数学」の語源となった著書『ジャブルとムカーバラの計算の書』の内容や、彼の名前が「アルゴリズム」の語源となったことについて、数学史における彼の重要な役割を分かりやすく説明しています。

7世紀インドの数学者ブラーマグプタの生涯と功績を解説。世界初めて0を数として扱い計算に適用した革命的業績、ブラーマグプタの公式の発明、二次方程式の解法一般化など、現代数学の基礎を築いた偉大な数学者の全貌を分かりやすく紹介。

ローマ時代の偉大な数学者、ディオファントスは「代数学の父」と称され、その数学的遺産は現代にまで引き継がれています。本記事では、彼の代表作である『算術』における未知数と方程式の記号導入がいかに画期的であったかを解説。アレクサンドリアの学術的背景や「ディオファントスの墓碑銘」問題にも触れながら、彼の生涯と業績の全体像を深く掘り下げます。数学史におけるディオファントスの重要性と、彼が代数学の発展に与えた多大な影響を詳しくご紹介します。

この記事では、古代ギリシャの数学者テアイテトスが無理数に関する研究と、正多面体に関する業績について紹介しています。テアイテトスがどう無理数を理解したのか、多面体の研究がどんな影響をプラトンに与えたのかを知ることができます。

キュレネのテオドロスは、√2から√17にあたる数が無理数であることを証明しました（√4と√9、√16以外）。彼が使用した「テオドロスの螺旋」と呼ばれる図形から、なぜ√17までだったのかを解き明かしています。

　$~5^2~$,$~15^2~$,$~25^2~$,‥‥$~95^2~$などの一の位が$~5~$である自然数の2乗は、非常に簡単に計算することができます。 　実は、十の位が$~a~$、一の位が$~5~$である自然数を2乗すると、以下のような計算結果となります。 下２桁が$~25~$ 百の位が$~a(a...

　中学受験で登場する「ヒポクラテスの定理」。この定理は今から約2500年前に生まれ、曲線図形の面積が直線図形の面積と等しくなるという観点から、当時のギリシャに大きな衝撃を与えました。この記事では、その歴史について触れながらも定理の内容やその証明、応用例について解説します。

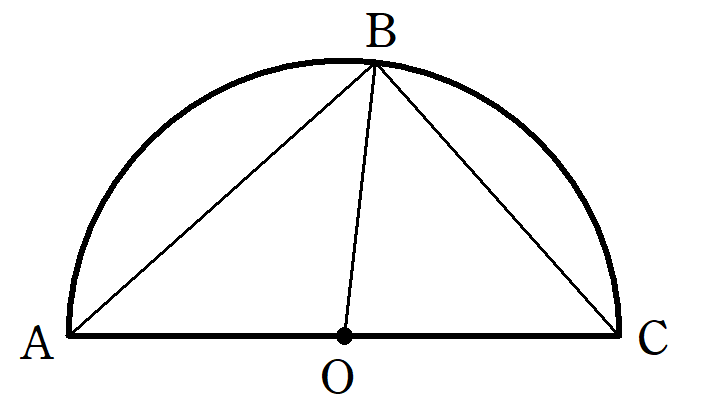
　世界で最初に証明された定理は「タレスの定理」であり、「半円に内接する三角形は直角三角形である」という内容です。実は、タレスの定理と呼ばれる定理は他にもあり、すべて現在の中学レベルの内容でした。それらの紹介と共に、タレスの定理が後世の数学にどのような影響を与えたのかを解説します。