$~5^2~$,$~15^2~$,$~25^2~$,‥‥$~95^2~$などの一の位が$~5~$である自然数の2乗は、非常に簡単に計算することができます。
実は、十の位が$~a~$、一の位が$~5~$である自然数を2乗すると、以下のような計算結果となります。
- 下2桁が$~25~$
- 百の位が$~a(a+1)~$
この記事では、その計算方法をたくさんの例を用いて解説するだけでなく、成り立つ理由まで現役数学教員が解説!
小学生でも理解できる証明もあるので、計算の原理まで理解して計算スピードを上げましょう!
一の位が5である自然数の2乗の計算方法
計算方法とその具体例
この記事の冒頭で示した通り、一の位が$~5~$である自然数の2乗は、以下のように計算が可能です。
一の位が$~5~$で、十の位が $~a~$ の自然数の2乗を計算すると、次のような計算結果となる。
- 下2桁が$~25~$
- 百の位が$~a(a+1)~$
百の位の導き方が少々わかりづらいので、具体例を見てみましょう。
例1:$~35^2~$
一の位が$~5~$、十の位が$~3~$なので、計算結果の下2桁は$~25~$、百の位は$~3\times(3+1)=12~$となる。
よって、$~35^2=12\times 100+25=1225~$。
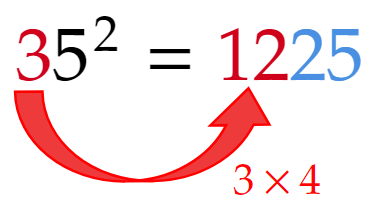
例2:$~65^2~$
一の位が$~5~$、十の位が$~6~$なので、計算結果の下2桁は$~25~$、百の位は$~6\times(6+1)=42~$となる。
よって、$~65^2=42\times 100+25=4225~$。
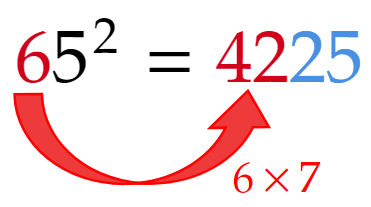
例3:$~125^2~$
一の位が$~5~$、十の位が$~12~$なので、計算結果の下2桁は$~25~$、百の位は$~12\times13=156~$となる。
よって、$~125^2=156\times 100+25=15625~$。
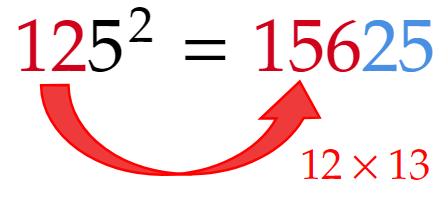
このように、連続する2つの整数の積と$~25~$を組み合わせるだけで、一の位が$~5~$である自然数の2乗は簡単に計算できます。
例3のように、3ケタの数であろうと同様の方法で計算可能です。

ただ、3ケタになると$~12\times 13~$のような暗算がしづらい‥‥。



ただ、十の位が$~1~$どうしであれば、暗算は可能だよ。
一の位が5である自然数の2乗を計算してみよう
規則性がわかったところで、実際に計算スピードを実感してみましょう!
$~105^2~$までは瞬時に計算ができるはずです。
| 式 | = | 計算結果 |
| $~5^2~$ | ||
| $~15^2~$ | ||
| $~25^2~$ | ||
| $~35^2~$ | ||
| $~45^2~$ | ||
| $~55^2~$ | ||
| $~65^2~$ | ||
| $~75^2~$ | ||
| $~85^2~$ | ||
| $~95^2~$ | ||
| $~105^2~$ | ||
| $~205^2~$ | ||
| $~1005^2~$ |



慣れると簡単!
そして、速い!
一の位が5である自然数の2乗の計算方法の証明
一の位が$~5~$である自然数の2乗を瞬時に計算できる今回の方法。
中学生以上が理解できる文字式を使った証明方法と、小学生でも理解できるような図形の面積を用いた証明方法の2通りで示します。
証明方法①:文字式を使った証明
使うのは中学3年生で習う式の展開の公式です。
$~a~$ を$~0~$以上の整数として、下1桁が$~5~$の自然数は$~10a+5~$と表せる。
この自然数の2乗は、
\begin{align*}(10a+5)^2&=100a^2+100a+25 \\
&=100(a^2+a)+25 \\
&=100\{ a(a+1) \}+25
\end{align*}となるため、下2桁が$~25~$、百の位が$~a(a+1)~$であることが示された。 $~\blacksquare $
十の位$~a~$がいくつだとしても、$~100~$倍しているため下2桁の$~25~$は保証されます。
展開公式を使いつつも、目的の形にするために因数分解も使っているため、中学3年生の証明の練習にもなるでしょう。



数学好きな生徒を集めた講習で、このネタの証明を扱いました。
証明方法②:正方形の面積を使った証明
小学生向けということで、$~25 \times 25=625~$という具体例で証明します。
一辺の長さが$~25~$の正方形の面積を考える。
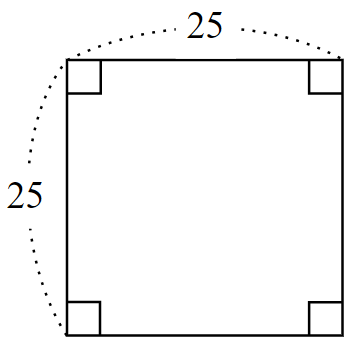

この正方形の右上の角に合わせて、縦$~20~$、横$~5~$の長方形を切り取る。
切り取った長方形の向きを変え、左下の角に合わせてつなげる。
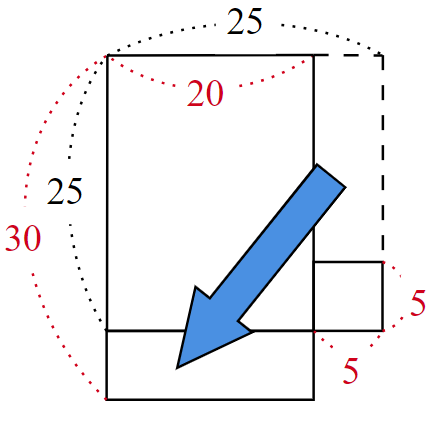

これにより求めたい面積は、縦$~30~$、横$~20~$の長方形と一辺の長さが$~5~$の正方形の和となる。
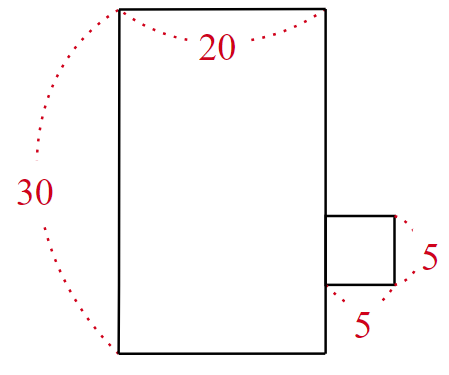

そのため、
\begin{align*}
25 \times 25&=20 \times 30 + 5 \times 5 \\
&=600+25 \\
&=625
\end{align*}と計算できることが示された。 $~\blacksquare $
中学生以上であれば、$~35~$を$~10a+5~$と置き換えることで一般化ができます。
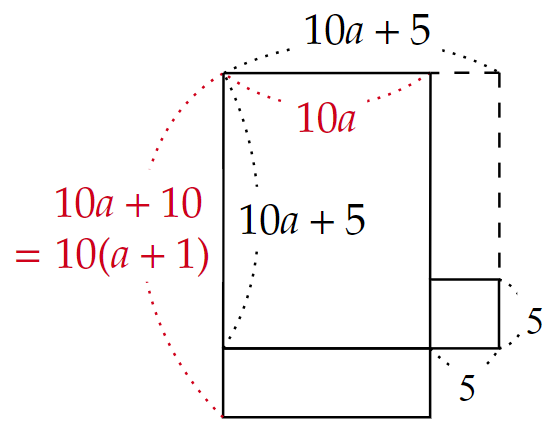

\begin{align*}
(10a+5)^2&=10(a+1) \times 10a + 5 \times 5 \\
&=100a(a+1)+25 \\
&=100\{a(a+1)\}+25 \\
\end{align*}この証明方法であれば、中学2年生からでも理解ができるでしょう。



面積だとイメージしやすいね。
まとめ
この記事では、一の位が$~5~$である自然数の2乗を瞬時に計算する方法を紹介しました。
- $~(10a+5)^2=100{a(a+1)}+25~$
- 証明は、式の展開と因数分解によって可能。
- 平方数を正方形の面積に置き換えて証明することもできる。
この計算テクニックは、他の計算テクニックと合わせると使用する機会が多いです。
是非この機会に習得してしまいましょう!



他の計算テクニック?



例えば、和と差の積。
$~13\times17~$では、$~15^2-2^2~$を計算すればよいため、$~15^2~$が瞬時に計算できれば、この計算も簡単だよ。


コメント
コメント一覧 (2件)
こんなに簡単にできるものがあるとは…もっと早くに教わりたかったです><
コメントありがとうございます。
地味に使えるんですよね。
下の例のように、計算の工夫と合わせると適用範囲がUPします。
$~23 \times 27~$
$~= (25-2) \times (25+2)~$
$~=25^2-2^2 ~$
$~=625-4 ~$
$~=621~$