中学受験で登場するヒポクラテスの三日月。
紀元前5世紀から存在するこの定理が、どんな内容でなぜ成り立つのかを正確に説明できますか?
この記事では、ヒポクラテスの三日月と呼ばれる図形の性質とその2つの応用例について、たくさんの図と共に解説!
そもそもなぜこのような図形が、紀元前に研究されたかということも含めて説明しています。
実は、ヒポクラテスの三日月は有名問題を解決するために研究され、当時としては画期的な成果を上げた図形なんです。
ヒポクラテスの三日月とは?
「ヒポクラテスの三日月」とは、キオスのポクラテス(Hippocrates , B.C.470頃~B.C.410頃)が円積問題解決のために用いた図形のことです。
1つの円の面積と等しい面積をもつ正方形を作図しなさい。
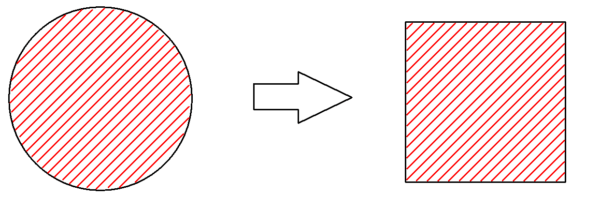
ヒポクラテスの三日月は曲線図形を直線図形に変換した世界初の例であり、円積問題の解決につながることが期待されました。
ヒポクラテスの三日月に出てくる「月形」
まず、ヒポクラテスの三日月でよく登場する図形が月形で、以下のような定義で与えられます。
二つの円弧で三日月形に囲まれた図形のことを月形という。
月形という名前ですが、満月(円)や半月(半円)は含みません。
さらに、三日月形に囲まれる必要があるので、十三夜月や小望月と称されるような月の形もNGです。

小さい2つの月形の和が大きい月形と等しい
では、ヒポクラテスが考えた月形の性質を見てみましょう。
直角三角形について、各辺を直径とする半円を描く。
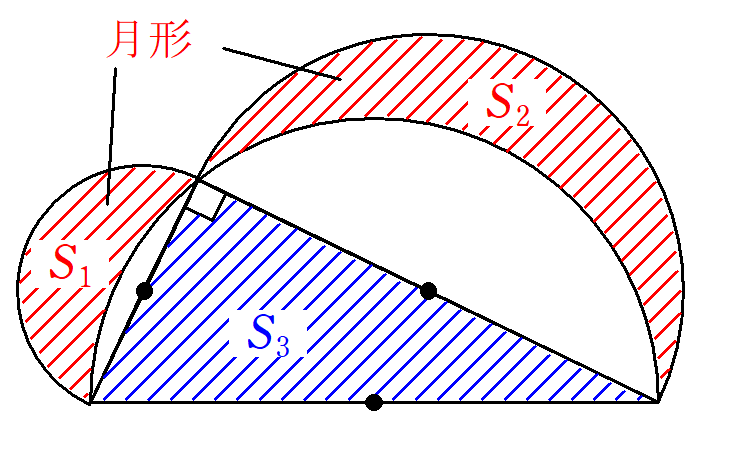
このとき、月形の面積の和と直角三角形の面積は等しくなる。
S_1+S_2=S_3
月形という曲線で囲まれた図形が、直角三角形という面積の求めやすい直線図形に変換されるため、当時としては革新的な定理でした。
三平方の定理により証明できる
ヒポクラテスの定理の証明は、図形を組み合わせて三平方の定理を使うだけの簡単なものです。
図4のように、$~S_1~$~$~S_3~$以外の部分の面積を、それぞれ$~P~,~Q~$と定める。
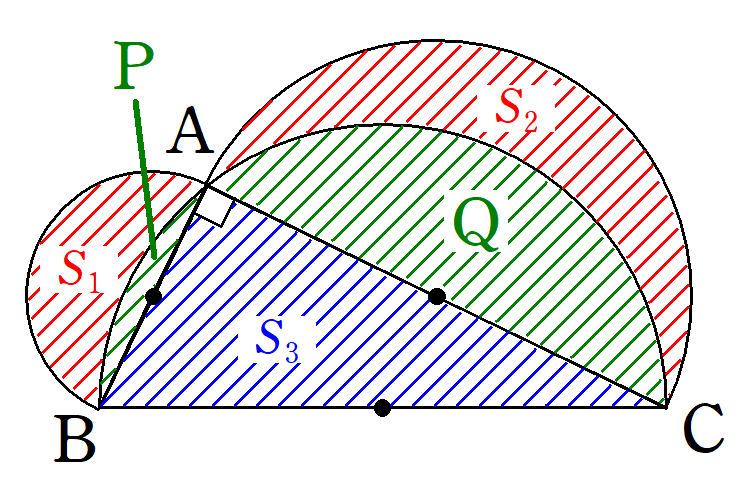
$~S_1+P~$、$~S_2+Q~$、$~S_3+P+Q~$はそれぞれ、直径$~AB~$、$~AC~$、$~BC~$の半円の面積となるため、
\begin{align*}
S_1+P&=\left(\frac{AB}{2} \right)^2 \cdot \pi \cdot \frac{1}{2}=\frac{AB^2}{8}\pi \\
\\
S_2+Q&=\left(\frac{AC}{2} \right)^2 \cdot \pi \cdot \frac{1}{2}=\frac{AC^2}{8}\pi \\
\\
S_3+P+Q&=\left(\frac{BC}{2} \right)^2 \cdot \pi \cdot \frac{1}{2}=\frac{BC^2}{8}\pi \\
\end{align*} である。
三平方の定理より、$~AB^2+AC^2=BC^2~$であることを利用し、$~S_1+P+S_2+Q~$を変形すると、
\begin{align*}
&~~~S_1+P+S_2+Q \\
\\
&=\frac{AB^2}{8}\pi +\frac{AC^2}{8}\pi \\
\\
&=\frac{AB^2+AC^2}{8}\pi \\
\\
&=\frac{BC^2}{8}\pi \\
\\
&=S_3+P+Q
\end{align*}となるため、
\begin{align*}
S_1+P+S_2+Q&=S_3+P+Q \\
S_1+S_2&=S_3
\end{align*}が示された。$~~\blacksquare~$
月形や直角三角形を半円にしたうえで、三平方の定理を使うだけの証明でした。
ヒポクラテスの定理の応用例
ヒポクラテスは自身の定理を利用し、円積問題解決に向けての研究を進めました。
円積問題の解決には至らなかった(実際は解決不可)ものの、様々な成果がありました。

半円の弧の月形を正方形で表す
まず、半円の弧を含む月形を正方形で表すことに成功しました。
図5の赤い斜線部分の月形の面積は、青い斜線部分の直角二等辺三角形の面積と等しい。
-1024x459.png)
すなわち、円の半径を一辺とする正方形の面積と等しいことになり、円積問題のゴールに近づきます。
証明は以下のようにできます。
図6のように、各部分の面積を$~S_1~$~$~S_4~$と定める。
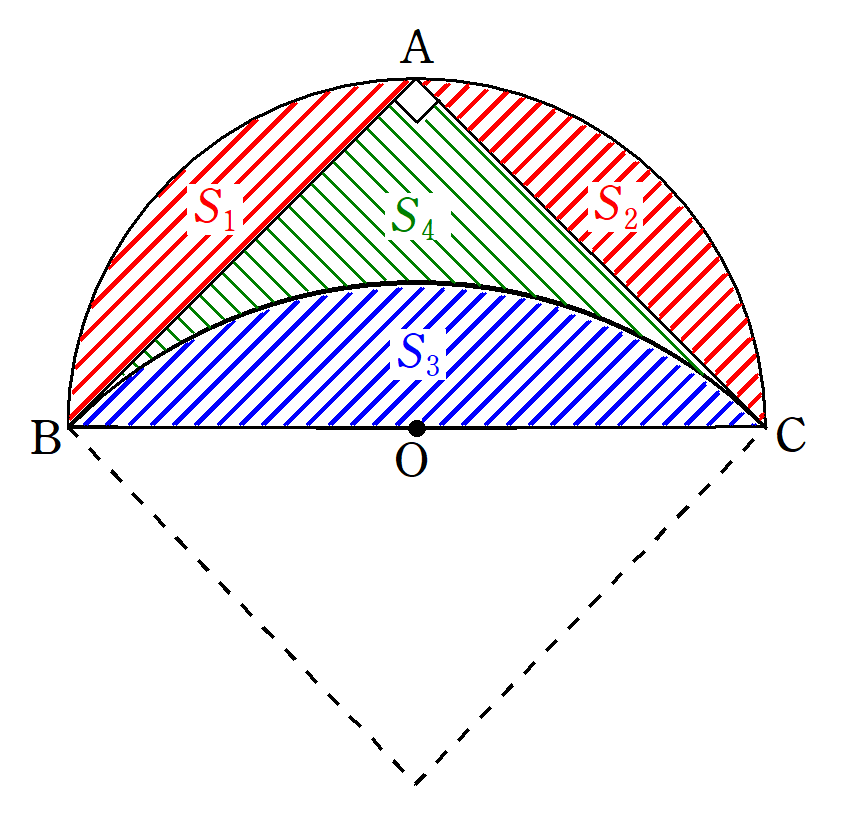
まず、$~S_1~$を考える。
.png)
扇形から直角二等辺三角形$~OAB~$をひけばよいので、
\begin{align*}
S_1&=\frac{BO^2}{4}\pi-\frac{BO^2}{2}~~~~\cdots①
\end{align*} と求まる。
$~S_1~$と$~S_2~$は対称な図形なので、
\begin{align*}
S_2&=\frac{BO^2}{4}\pi-\frac{BO^2}{2}~~~~\cdots②
\end{align*} である。
また、$~S_3~$を考える。
.png)
扇形から直角二等辺三角形$~O^{\prime}BC~$をひけばよい。
$~BO^{\prime}=\sqrt{2}BO~$、すなわち$~\left(BO^{\prime}\right)^2=2BO^2~$であることを利用すると、
\begin{align*}
S_3&=\frac{\left(BO^{\prime}\right)^2}{4}\pi-\frac{\left(BO^{\prime}\right)^2}{2} \\
\\
&=\frac{2BO^2}{4}\pi-\frac{2BO^2}{2} \\
\\
&=\frac{BO^2}{2}\pi-BO^2 ~~~~\cdots③
\end{align*} と求まる。
$①$~$③$より、
S_1+S_2=S_3
となり、両辺に$~S_4~$を加えることで、
\begin{align*}
S_1+S_2+S_4&=S_3+S_4 \\
(月形)&=(直角二等辺三角形ABC)
\end{align*}が示された。$~~\blacksquare~$
半円を台形と月形の差で表す
次に、ヒポクラテスは半円そのものを台形と月形で表しました。
図9のように、弧$~BC~$を三等分する点を$~A~,~D~$とし、線分$~BA~,~AD~,~DC~$を直径とする半円をそれぞれ描く。
このときに表される合同な月形の面積を$~S_1~$、合同な正三角形の面積を$~S_2~$とすると、$~AB~$を直径とする半円$~O^{\prime}~$の面積は以下の式で表すことができる。
(半円O^{\prime})=3S_2-3S_1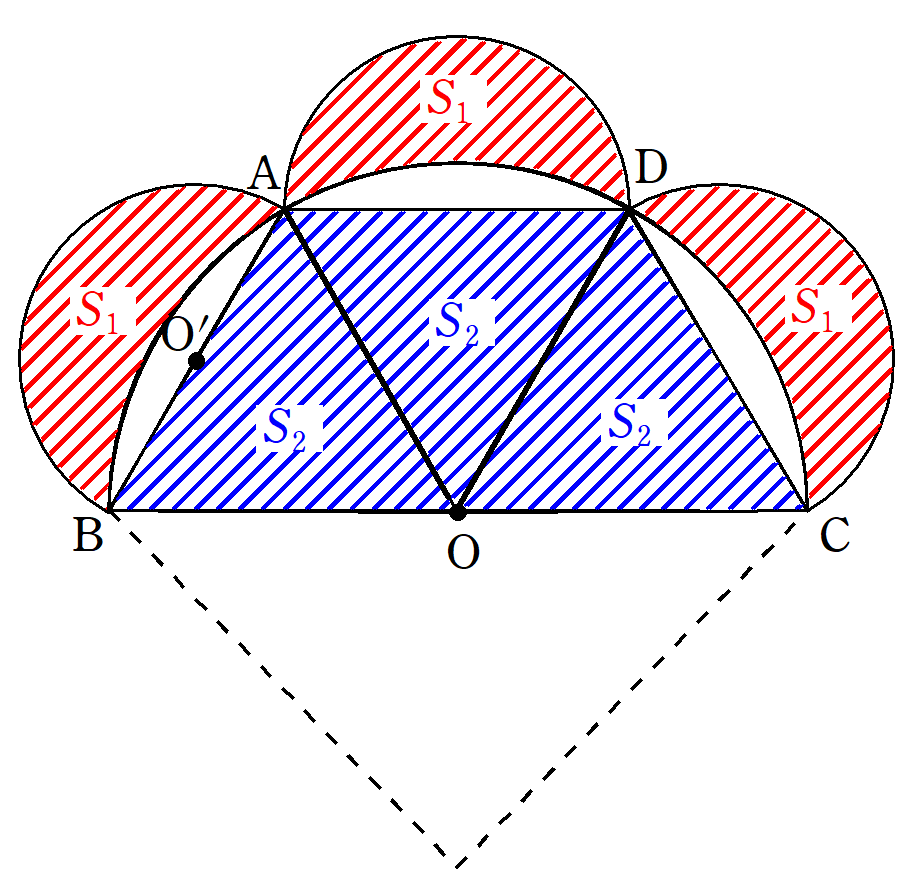
半円$~O^{\prime}~$が、$~台形ABCD~$と月形3つ分の差で表されるとわかります。
注意しなくてはならないのは、元の大きな半円$~O~$ではなく、新たに作った半円$~O^{\prime}~$であるということです。
図10のように、残った合同な図形の面積を$~S_3~$とする。
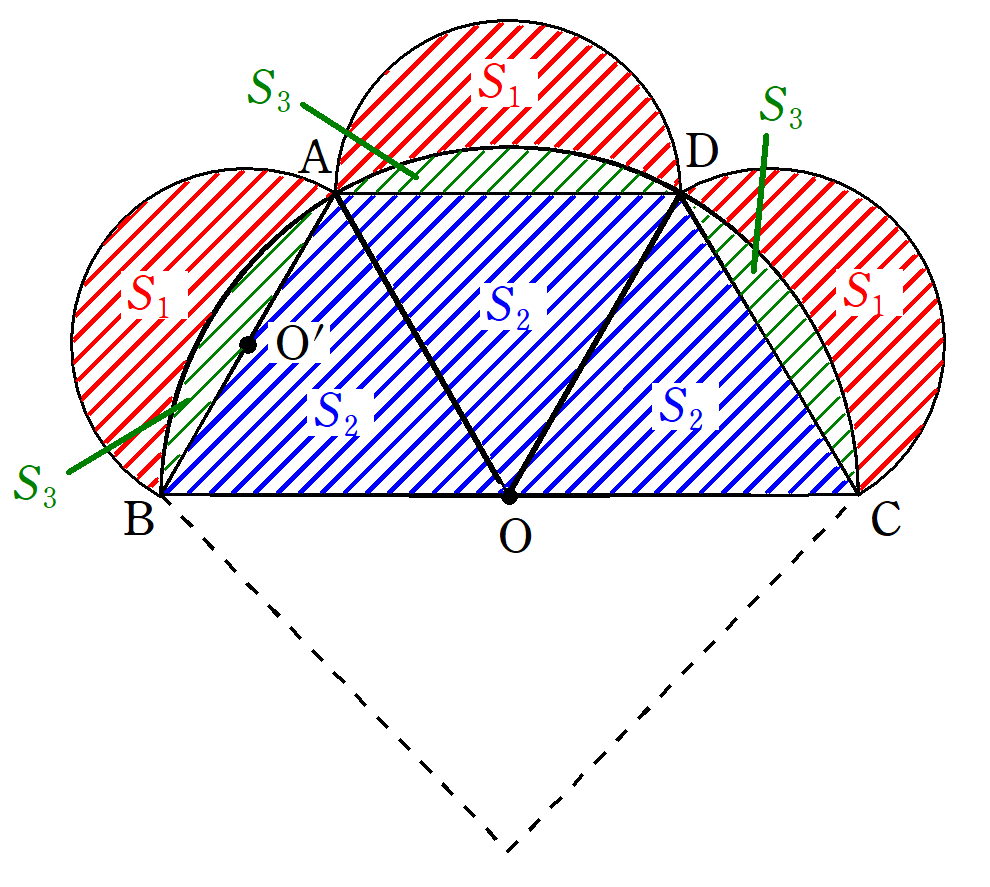
半円$~O^{\prime}~$と半円$~O~$は相似であり、相似比は$~1:2~$。
ゆえに面積比は$~1:4~$なので、
\begin{align*}
1:4&=(S_1+S_3):(3S_2+3S_3) \\
4S_1+4S_3&=3S_2+3S_3
\end{align*}となる。
ここで、左辺を$~S_1+S_3~(=半円O^{\prime})~$にするために、両辺から$~3S_1~$と$~3S_3~$をひくと、
S_1+S_3=3S_2-3S_1
であり、求めたい式が示された。$~~\blacksquare~$
ヒポクラテスの誤り?
応用例1と応用例2の組み合わせにより、一見すると円積問題が解けたような誤解が生まれます。
その誤解とは、以下のような議論からなります。
- 応用例2により、半円は台形と月形の差で表される。
- 応用例1により、月形は直角二等辺三角形で表される。
↓
半円は、台形と直角二等辺三角形の差、つまり直線図形だけで表される。
部分的に切り取ると成り立っているように思えますが、応用例1で扱っている月形と応用例2で扱っている月形は全くの別物であるため、この議論は成り立ちません。
ヒポクラテスが以上の議論により円積問題を解けたと結論付けた、と哲学者アリストテレス(Aristotle ,B.C.384-322)は自身の著書の中で、ヒポクラテスを揶揄しています。

(出典:After Lysippos, Public domain, via Wikimedia Commons)
アリストテレスは、ヒポクラテスが税関に騙されて大金を失ったことにも触れ、以下のように彼を評しています。
人間はある方面には間抜けでも、他の面ではそうではないことがあるものである。
『素顔の数学者たち』p8より引用
ヒポクラテスは、幾何学では優れていたが他のことでは気弱でお人好しであったため、ビザンティンで税の徴収人にだまされて大金を失った。
ヒポクラテスの月形研究の成果は認めつつも、彼の注意力の無さを指摘しています。
まとめ
ヒポクラテスの定理とその応用例について解説してきました。
- ヒポクラテスの定理は、曲線図形の月形を直線図形に変換する定理。
- 三大作図問題の1つである円積問題を解決するために研究された。
- 応用することで、円積問題の解決につながりそうな結論が得られた。
円積問題自体は、1882年にドイツの数学者フェルディナンド・フォン・リンデマン(Ferdinand Von Lindemann, 1852-1939)によって、作図不可能と証明されました。
しかし、その2000年前に生まれたヒポクラテスの定理は、当時のギリシャを中心に大きな衝撃を与えた内容と言えるでしょう。
ヒポクラテスについてもっと知りたい方は、以下の記事もご覧ください。

◇参考文献等
・河田直樹(2006)『古代ギリシアの数理哲学への旅』,pp191-195,現代数学社.
・片野善一郎(2005)『素顔の数学者たち』,p8 , 裳華房.

コメント