伝統的な西洋の時代区分では、476年の西ローマ帝国滅亡から、1453年の東ローマ帝国の滅亡あたりまでを指す「中世」。
この約1000年という長い期間は、数学において闇と光が同居する時代でした。
数学史における中世を3つに分けてみると、次のように大別できます。
- 古代知識の保存と継承（5〜10世紀）
- イスラーム数学の流入と大学の誕生（11,12世紀）
- 独自の発展と革新（13〜15世紀）
古代の知識の継承と保存に徹した中世初期という暗黒時代、イスラーム数学という光が差し込んだ中世中期、それをヨーロッパ独自のものへと発展させた中世後期の数学についてを、この記事では数学史の先生Fukusukeがざっくりと解説！
中世ヨーロッパの数学がたどった壮大な軌跡を、世界史の流れとともに見ることができます。
Fukusuke（ふくすけ）
数学史の先生
- 現役の中学・高校数学教員
- 著書2冊
重刷、ブログ累計200万PV達成 - 行間がなくなるほど丁寧な式変形で執筆中
Fukusuke（ふくすけ）
数学史の先生
- 現役の中学・高校数学教員
- 著書2冊は発売1ヶ月で即重刷
- 当数学史ブログは累計200万PV達成
- 行間がなくなるほど丁寧な式変形で記事を執筆
『世界を変えた数学史図鑑』『教養としての数学史』好評発売中！
丸善日本橋店の2025年ベストセラー（理工書部門）に選ばれました！
（理工書部門）に選ばれました！
中世ヨーロッパの数学史年表
| 年代 | 数学史上の出来事 | 世界史上の出来事 |
|---|---|---|
| 391年 | アレクサンドリア図書館がキリスト教徒によって破壊される | |
| 395年 | ローマ帝国の東西分裂 | |
| 415年 | ヒュパティアが死亡する →アレクサンドリアから学者が消えていった | |
| 476年 | 西ローマ帝国滅亡 | |
| ↑「古代ローマ」という時代の終焉↑ | ||
| 480年頃 | ボエティウス誕生 | |
| 524年頃 | ボエティウス、ユークリッド『原論』などを翻訳・要約 | |
| 529年 | アカデメイアが閉鎖される | |
| 735年頃 | アルクィン誕生 | |
| 800年 | カールの戴冠（西ローマ帝国復活） | |
| 843年 | ヴェルダン条約、フランク王国分裂 | |
| 1085年 | レコンキスタでトレド陥落、翻訳活動が活発化 | |
| 1088年 | ボローニャ大学設立 | |
| 1096年 | 第1回十字軍開始 | |
| 1170年頃 | フィボナッチ誕生 | |
| 1202年 | フィボナッチ『算盤の書』執筆 | |
| 13世紀前半 | ヨルダヌス・ネモラリウスが活躍 | |
| 1288年 | ゲルソニデス誕生 | |
| 1290年 | トーマス・ブラドワディーン誕生 | |
| 1292年頃 | ウォリングフォードのリチャード誕生 | |
| 1328年 | ブラドワディーン『比の理論』執筆 | |
| 1336年 | ウォリングフォードのリチャード死去 | |
| 1337年 | 百年戦争開始 | |
| 1342年 | ゲルソニデス、数学的帰納法を用いた証明を残す | |
| 1347年 | ペスト（黒死病）の大流行 | |
| 1349年 | ブラドワディーン死去 | |
| 1360年頃 | ニコル・オレーム、運動のグラフ化を考案 | |
| 1382年 | ニコル・オレーム死去 | |
| 1453年 | 東ローマ帝国滅亡、百年戦争終結 | |
中世ヨーロッパの歴史と数学史
古代知識の保存と継承（5世紀〜7世紀）
西ローマ帝国の崩壊後、ヨーロッパは政治的・社会的な混乱期に突入し、人々は心の拠り所を得ようとキリスト教の影響力が強まっていきました。
神学が重視されたこの時代、数学はキリスト教の行事である復活祭の日付計算に使われる程度の、実用的な目的に終始しています。
この「科学の暗黒時代」において、古代ギリシャ・ローマの貴重な知識を保存し、次代へと受け継ぐ重要な役割を担ったのが、ボエティウスです。
彼はニコマコスの『算術入門』やユークリッドの『原論』などのギリシャの著作を、ラテン語に翻訳・要約し、中世の知識人にとって不可欠な教科書を提供しました。
この教科書はほとんどが初歩的な内容ではありましたが、500年以上にわたって修道院学校で使われ、古代の知識をかろうじて中世ヨーロッパにつなぎとめました。
古代数学とイスラーム数学への関心（8世紀〜10世紀）
8世紀末になると、フランク王国のカール大帝のもとで「カロリング・ルネサンス」と呼ばれる文化復興運動が起こります。
その中心人物となったのが、イングランド出身の学者アルクィンでした。
彼はカール大帝に招かれ、聖職者たちが春分の日や満月の日を計算できるような数学教育を施すよう命じられたのです。
（出典：Fulda, Public domain, via Wikimedia Commons）
キリスト教の行事のためと言えど、数学の必要性が再認識され、古代ギリシャやローマの数学の文献が書き写される動きが多くの修道院で起こりました。
カロリング・ルネサンスから約200年後。
10世紀末にローマ教皇となるジェルベールという人物が現れます。
（出典：Artaud de Montor (1772–1849), Public domain, via Wikimedia Commons）
彼は初めてイスラーム世界から数学を学んだキリスト教徒です。
イスラーム数学をヨーロッパに広めようとしたものの、数学への関心が依然薄かったことなどを理由に、大きな影響を与える結果にはなりませんでした。
イスラーム数学の流入と大学の誕生（11世紀〜12世紀）
11世紀から12世紀にかけて、ヨーロッパ世界は大きな転換期を迎えます。
十字軍やイベリア半島でのレコンキスタ（国土回復運動）を通じて、当時世界最先端の文化を誇っていたイスラーム世界との接触が活発化したのです。
特に1085年にキリスト教徒が奪還したスペインの都市トレドは知識の交流拠点となり、さまざまな翻訳者がアラビア語で書かれた古代ギリシャの主要な数学書をラテン語に翻訳しています。
| 翻訳者 | 活躍した年代 | 翻訳書（代表的なもの） |
|---|---|---|
| バースのアデラード | 1116-1142頃 | フワーリズミー『天文表』 ユークリッド『原論』 |
| クレモナのジェラルド | 1150-1185頃 | ユークリッド『原論』 アルキメデス『円の計測』 プトレマイオス『アルマゲスト』 フワーリズミー『ジャブルとムカーバラの書』 |
| チェスターのロバート | 1141-1150 活躍 | フワーリズミー『ジャブルとムカーバラの書』 |
（出典：See page for author, Public domain, via Wikimedia Commons）
また、この知的興奮は新たな学びの場である「大学」の誕生を促しました。
ボローニャ、パリ、オックスフォードといった都市に次々と大学が設立され、神学や法学とともに数学も教えられるようになります。
大学は、学者たちが集い、議論し、新たな知識を探求する中心地となり、後の数学の発展における重要な土台となりました。
独自の発展と革新（13世紀〜14世紀）
イスラーム世界から受け継いだ知識を土台に、13世紀以降のヨーロッパでは数学が独自の発展を遂げ始めます。
- 商業の発展を目的に、インド・アラビア数字の実用性がヨーロッパ全土に広がっていった。
- スコラ哲学が隆盛し、論理的思考法が数学研究に応用された。
- 数を文字で表すという記号代数学や、証明における数学的帰納法が誕生し始めた。
- オックスフォード大学で、物体の運動を数学的に記述する動きがあり、比の理論が発展した。
- 速さと時間を図形で表すことにより、グラフの概念が初めて生まれた。
上記に挙げた例は、それまでの時代のように古代や他地域からの知識の継承ではなく、ヨーロッパが独自に数学を発展させたことを示しています。
そして、その後はヨーロッパを中心に数学が発展していくことになりました。
中世ヨーロッパの独創的な数学者たち
ボエティウスやアルクィン、ジェルベールも数学者として数えられますが、彼らの主な功績は知識の継承と伝播です。
ここでは、12世紀以降のヨーロッパにおいて、数学を独自に発展させていった数学者たちを取り上げていきます。
フィボナッチ（1170年頃〜1250年頃）
イタリアのピサの商人であったフィボナッチは、中世ヨーロッパを代表する数学者です。
（出典：Deep also it at it.wikipedia, Public domain, via Wikimedia Commons）
フィボナッチは北アフリカでイスラーム世界の進んだ数学に触れ、その知識をヨーロッパに紹介しました。
彼の主著『算盤の書』は、インド・アラビア数字とそれを用いた筆算の方法を詳説したもので、商業計算の効率を飛躍的に高め、ヨーロッパ社会に大きな変革をもたらしました。
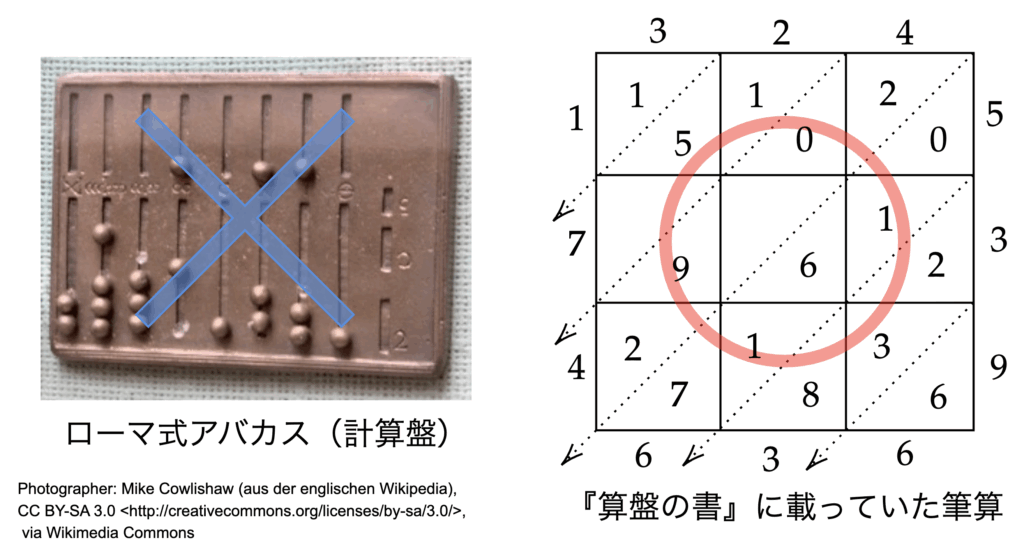
また、同書で紹介されたウサギの問題では、解法の中で「フィボナッチ数列」が登場し、後世の数学者たちに多くのインスピレーションを与え続けています。
ヨルダヌス・ネモラリウス（13世紀前半）
ヨルダヌス・ネモラリウスは、中世ヨーロッパにおける代数学の発展に大きく貢献した数学者です。
彼は、以下のようなルールのもとで文字式を使い、二次方程式の解法を代数的に解いています。
- 既知数は$~a~,~b~,~c~$、未知数は$~x~,~y~,~z~$ではなく、登場順にアルファベット順
- $~+~$や$~-~$の演算記号はない
- $~ab~$が一つの数を表すこともあれば、足し算を表すこともある
- アラビア数字は使わず、ローマ数字を使った
現在の文字式のルールに比べれば分かりづらいものの、文字を使って計算するという近世ヨーロッパ数学の先駆けとなる取り組みでした。
幾何学的に二次方程式の解を求めていたアル・フワーリズミーやサービト・イブン・クッラによるイスラーム数学から、中世ヨーロッパ数学が一歩先に進んだ瞬間と言えるでしょう。
トーマス・ブラドワディーン（1290年〜1349年）
トーマス・ブラドワディーンは、オックスフォード大学マートン学派の中心人物で、「深遠博士」の異名を持つ神学者兼数学者です。
彼はアリストテレスの運動法則を数学的に定式化し直し、速さは力と抵抗の「比の比」によって決まるという、より洗練された法則を提唱しました。
速さ$~V~$は力$~F~$の対数に比例し、抵抗$~R~$に対して、対数的に減少する。
すなわち、$~K~,~a~$を比例定数として、
V = K \log_a\left(\frac{F}{R}\right)~~~\cdots※と表される。
※ブラドワディーンは上記のように対数を使った訳ではなく、速さを2倍するには、力と抵抗の比（の値）を2乗する必要があると説明した。また、現代の力学において、ブラドワディーンの運動法則もアリストテレスと同様、間違っていた。
この理論を展開する中で、ブラドワディーンは比の値を2乗したり、比の値の平方根をとったりと、比で扱える数の範囲を広げる結果となりました。
ウォリングフォードのリチャード（1292年頃〜1336年）
ウォリングフォードのリチャードは、前述のブラドワディーンの同僚であり、同じくマートン学派の数学者です。
彼は、ブラドワディーンらが発展させた比の理論をさらに整備し、「デノミナティオ」という概念を定義しました。
比とは、同種の量二つの間にある関係である。
比で、一方が他方を割るとき、その結果をデノミナティオという。
これは現代でいう「比の値」にあたるもので、デノミナティオの概念を用いて比の合成を明確に定義しました。
ユークリッドは線分の配置などに基づいて幾何学的に比の合成を考えていたことに比べ、リチャードが定義した比の合成は非常にわかりやすく、運動学での計算がよりスムーズに行えるようになりました。
ゲルソニデス（1288年〜1344年）
ゲルソニデスは、南フランスで活躍したユダヤ人学者です。
ゲルソニデスという名前は、レヴィ・ベン・ゲルソンがラテン語化したものとなっています。
彼の功績としては、数学的帰納法を「1段1段限りなく上昇してゆくこと」と表現したうえで、この証明手法の本質を明確に表しました。
イスラームの数学者アルハゼンは、等式を証明するにあたって$~n=3~$を仮定したうえで$~n=4~$の証明を行っていましたが、任意の自然数で同じことができると、ゲルソニデスは著書の中で述べています。
また、この数学的帰納法から階乗$~!~$、順列$~P~$、組合せ$~C~$の公式を求めています。
ニコル・オレーム（1320年頃〜1382年）
ニコル・オレームは、14世紀に活躍したフランスの数学者です。
（出典：https://commons.wikimedia.org/wiki/File:Oresme-Nicole.jpg）
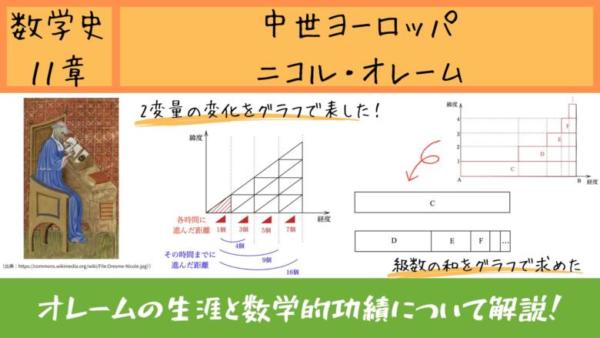
彼の最も大きな功績は、物体の運動のような変化する量を、横軸と縦軸を持つ座標系を用いて視覚的に表現する「グラフ」の概念を考案したことです。
水平な線に沿って時間の各瞬間を表す点をつけ、各瞬間に対して垂直方向に引いた線分の長さで速度を表す。
このとき、水平方向を経度と言い、垂直方向を緯度という。
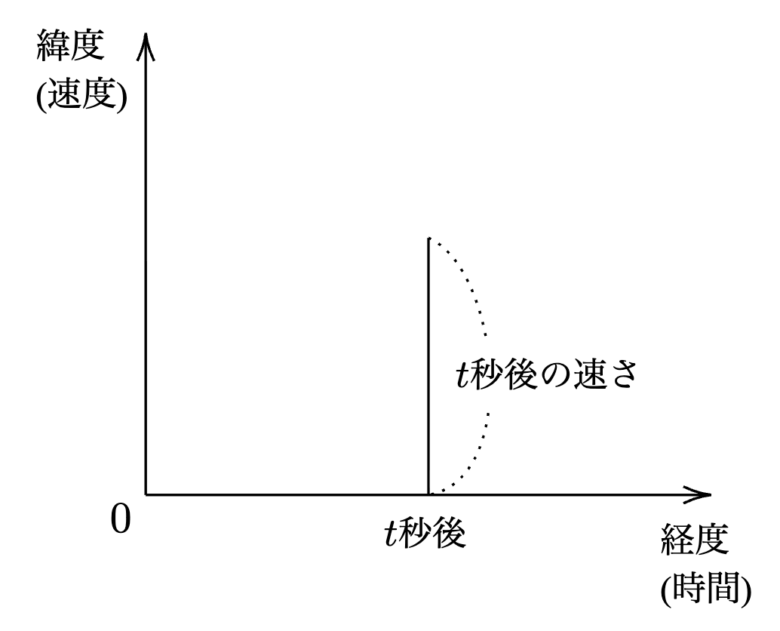
運動の様子をグラフとして視覚化することで、速度や加速度といった概念を幾何学的に捉えることが可能になりました。
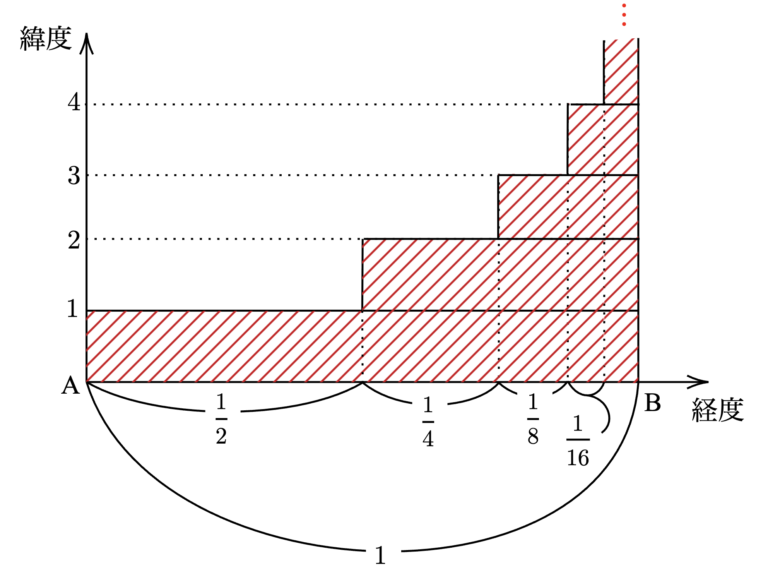
オレームは無限級数をもグラフ的に捉え、その面積の和から収束する値を求めています。
まとめ：イスラームの知を受け継ぎ、ルネサンスへ橋渡しした
476年から1453年という長い期間の中世ヨーロッパの数学は、暗黒時代と光が共存する時代でした。
古代知識の保存から始まり、イスラーム数学の流入、そしてヨーロッパ独自の数学発展へと進展し、ルネサンスへの橋渡しとなりました。
- ボエティウスが古代ギリシャの数学知識をラテン語に翻訳し、500年以上にわたって継承
- カール大帝のカロリング・ルネサンスで数学教育の必要性が再認識される
- 11〜12世紀のトレドでイスラーム数学の翻訳活動が活発化し、大学が誕生
- フィボナッチがアラビア数字をヨーロッパに紹介し、商業革命を支援する
- ヨルダヌス・ネモラリウスが文字式を使った証明を行う
- ブラドワディーンとリチャードが運動学を追究する中で比の理論を発展させる
- ゲルソニデスが数学的帰納法を一般化する
- ニコル・オレームがグラフの概念を発明し、無限級数にまで言及する
ギリシャから一度はイスラームに渡った数学が、ヨーロッパに再び帰ってきたんだね。
エジプトやバビロニアからギリシャへ、ギリシャからアレクサンドリアへ、アレクサンドリアとインドからイスラームへ、そしてイスラームから再びヨーロッパへ。
いよいよここからはヨーロッパが発展の舞台となるよ。
.jpg){kind=link}
コメント