ユークリッド原論の有名な命題5選！証明の最後にあるQEDの意味とは？

　ユークリッドの『原論』は、古代ギリシャの数学が網羅された、数学書や教科書の土台として今も根付いている名著です。

　『原論』はユークリッドによって紀元前300年頃に書かれ、聖書の次に版を重ねている書物と言われるほど、世界に流通しています。

　この本記事では、『原論』の構成とともに、特に有名な命題を5つ紹介し、その証明の最後に記される「QED」の意味についても解説！

　この記事を読むことで、数学の論理の厳密さを象徴する『原論』の有名部分を味わうことができます。

時代	紀元前300年頃
場所	アレクサンドリア

『原論』の構成

　『原論』は、ユークリッド（Euclid , 紀元前330年頃〜紀元前275年頃）によって書かれたギリシャ数学の集大成とも呼べる数学書です。

　この大著は、数学の基本原理を明確かつ体系的に提示しており、その後の数学に大きな影響を与えました。

５つの公理と5つの公準で始まる

　『原論』は、数学的な命題を証明するための基本的な前提条件、つまり公理と公準から始まります。

　ユークリッドは、5つの公理と5つの公準から、『原論』の論理を始めました。

　ユークリッドは、これらの公理と公準をもとにして、その後のすべての命題を論理的に導き出しています。

各章は定義と命題から構成される

　『原論』の冒頭で、公理と公準が述べられた後は、分野ごとで区切られた各章へと進みます。

　各章は、まずいくつかの定義から始まり、その後に命題が続きます。
　1章であれば23個の定義から始まっており、48個の命題が証明と共に載っているのです。

　最初の章の最初の命題では、中学1年生で行う作図の方法の正しさが述べられています。

　最初の命題ゆえに、公理と公準、定義のみを使って証明されています。

　続く命題2では、コンパスで同じ長さをとることの正しさが述べられています。

　この命題の証明で使えるのは、公理や公準、定義の他に、すでに証明済みの 『原論』1章　命題1 も含まれます。

　このように命題を証明していくことにより、どんどん使える命題が増えた状態で新たな命題の証明ができるようになります。

　『原論』に由来する今の数学は、まさに積み上げの学問と言えるでしょう。

全13章で様々な分野が扱われる

　『原論』は全13巻から成り立っており、各章の内容は以下の通りです。

章	タイトル	定義の数	命題の数	内容
1	平面図形の基礎	23	48	5つの公準、5つの公理もここに掲載。対頂角や平行線の錯角、合同条件などの基本的な知識の命題が中心。命題47にユークリッドが考えた三平方の定理の証明が載っている。
2	代数の公式	2	14	分配法則や展開公式、二次方程式の解の公式を図形によって証明している。
3	円	11	37	円に内接する四角形の性質や接線の性質など、円に関する基本定理を紹介。
4	円と正多角形	7	16	円に内接・外接する正多角形の作図が中心。命題11の正五角形の作図はピタゴラスによる。
5	比例論	18	25	エウドクソスの比例論。無理数を含めた連続量で考えることができる。
6	相似	4	33	相似な図形を考え、図形の中で比の性質を利用している。
7	数論①	11	39	6章までとは独立。最初の命題はユークリッドの互除法を扱っている。
8	数論②	なし	27	アルキュタスの研究成果が中心。等比数列を扱う。
9	数論③	なし	36	命題20で素数が無限に存在することを証明。命題21以降はピタゴラスの偶数と奇数に関する命題。また、命題36では完全数を導く公式が登場。
10	無理数	16	115	最も重要と考えられている章。テアイテトスによるものと考えられている。命題9で$~\sqrt{2}~$が無理数であることを証明。
11	空間図形の基礎	29	39	角錐や角柱の定義を含む。球の定義は半円を直径を軸に回転させた立体。
12	面積と体積	なし	18	エウドクソスの取りつくし法により証明される面積や体積の公式。
13	正多面体	なし	18	テアイテトスによる5つの正多面体について。外接球の直径も求めている。

　内容からもわかる通り、古代ギリシャで研究された、当時の数学の幅広い領域が網羅されていることがわかります。

有名な命題5選

ユークリッドの『原論』には数多くの重要な命題が含まれていますが、特に有名なものを5つ紹介します。

三平方の定理（『原論』1章　命題47）

　ピタゴラスが初めて証明をした三平方の定理（ピタゴラスの定理）は、直角三角形の各辺の長さに関する基本的な関係を示しています。

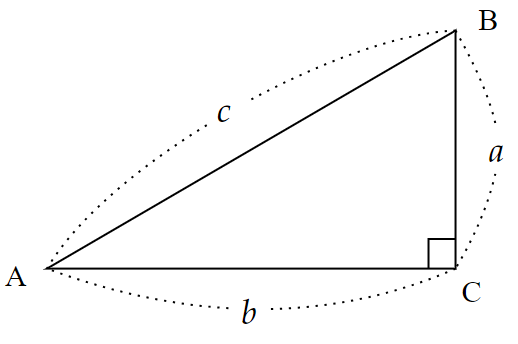
　『原論』における実際の文章としては、「直角三角形で、斜辺を一辺とする正方形は、直角をはさむ２辺をそれぞれ一辺とする正方形の和に等しい。」というように図形を使って記述されています。

　ユークリッドは『原論』を書く中で、ピタゴラスの証明方法とは異なる、オリジナルの証明方法を考えました。

　ユークリッドが使用した図のことを「花嫁の椅子」や「ユークリッドの風車」と呼んでいます。

　ユークリッドの証明方法は、三平方の定理の有名な証明の1つで、幾何学的な性質だけが用いられています。

正五角形の作図（『原論』4章　命題11）

　正五角形を作図する方法は、ユークリッドの『原論』でも説明されています。

　この作図方法は、ピタゴラスによるものとされ、彼の教団にとって神秘的な図形として崇められていました。

　4章の最後の命題では、正三角形と正五角形を組み合わせた正十五角形の作図方法まで言及されており、ユークリッドの応用力の高さを表していると考えられます。

ユークリッドの互除法（『原論』7章　命題1）

　ユークリッドの互除法は、二つの整数の最大公約数を求める効率的な方法として知られています。

　このアルゴリズムはユークリッドの名を冠していますが、テアイテトスが同様の方法で無理数かどうかを判定していたため、そこからヒントを得たのではないかと考えられます。

素数は無限に存在する（『原論』9章　命題20）

　ユークリッドは、素数が無限に存在することを証明しました。

　背理法を使った初期の1つの例で、ユークリッドは素数が$~A~,~B~,~C~$の3つしかないという仮定から始まり、それよりも大きい素数$~G~$を作り出して矛盾を導いています。

√2は無理数である（『原論』10章　命題9）

　同じく背理法を使った有名な例が、$~\sqrt{2}~$の無理数性の証明です。

　こちらはピタゴラス教団のヒッパソスに由来すると言われますが、どのような方法で行ったかは謎に包まれています。

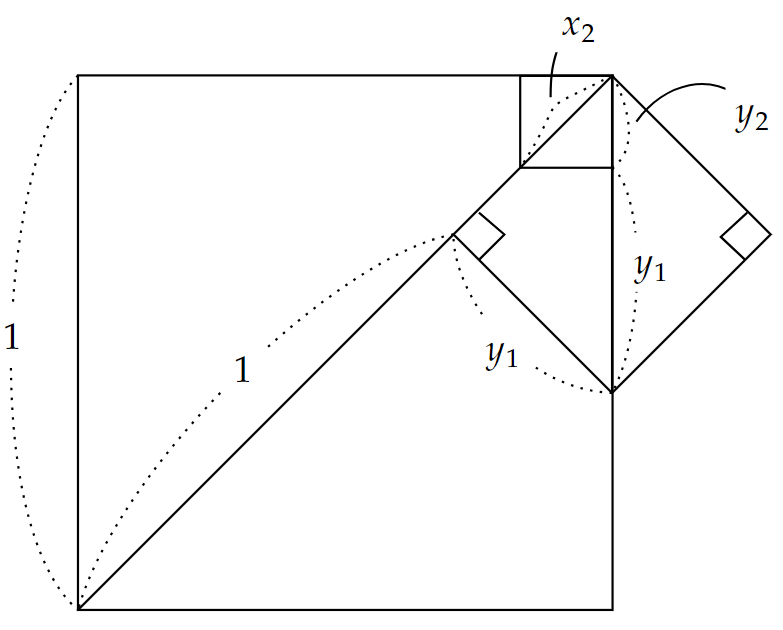
　『原論』では、一般化された形で無理数性の証明が行われました。

　要するに、正方形の面積比が平方数で表されなければ、どちらか一方の辺の長さは無理数であるということです。

　これにより、面積が$~1~$と$~2~$の正方形を考えると、$~1:2~$が平方数だけの比で表されないため、どちらか一方、すなわち$~\sqrt{2}~$が無理数であるとわかるのです。

証明の最後にあるQEDとは？

　ユークリッドは、『原論』の多くの命題の証明の最後に「Q.E.D.」の3文字を入れました。

　どのような意味を持っているのでしょうか？

Quod Erat Demonstrandum

　「Q.E.D.」を省略せずに書くと、ラテン語の “Quod Erat Demonstrandum” となり、「示されるべきことが示された」という意味を持ちます。

　『原論』において、数学的な証明や論理的な議論の終わりに「Q.E.D.」は使われており、ユークリッドのすぐ後のアルキメデスや、ルネサンス後のヨーロッパ、さらには現在に至るまで幅広く使用されています。

『原論』ではQEFも登場する

　『原論』では、「Q.E.F.」の3文字も登場します。

　こちらは、同じくラテン語の”Quod Erat Faciendum” となり、「行うべきことが行われた」という意味を持ち、幾何学的な構成や作図が完了したときに使用されます。

　『原論』以降も「Q.E.F.」が使われたと考えられていますが、ルネサンス以降は作図題よりも論理的な証明が重要視され、「Q.E.F.」を使う機会が減少。

　現在は、作図題であったとしても「Q.E.F.」を見かけることはほとんど無くなりました。

まとめ

　数学の歴史において欠かせない存在であるユークリッドの『原論』について解説してきました。

• 『原論』はユークリッドによって書かれた古代ギリシャ数学の集大成。
• 公理や公準、定義から各命題を証明していく体系性が徹底されている。
• ユークリッド独自の考察も『原論』の中で確認することができる。
• 各命題の最後でQ.E.D.やQ.E.F.が使用されている。