5~7世紀のヨーロッパの数学とは？ボエティウスやアンテミオスについて解説！【数学史11-1】

　古代ギリシャの数学が、ヒュパティアの悲劇的な死とともに終わりを告げた後、ヨーロッパの数学はどのような道を歩んだのでしょうか？

　一般的に「暗黒時代」と呼ばれるこの時期、西ヨーロッパでは古代の知識が失われ、数学は停滞したと考えられています。

　しかし、本当にヨーロッパ全土で数学の光は消えてしまったのでしょうか？

　この記事では、5世紀から7世紀にかけてのヨーロッパに焦点を当て、西と東で全く異なる運命をたどった東西ローマ帝国の数学の歴史を、数学史の先生Fukusukeが解説！

　西ヨーロッパで古代の知識を必死に守ろうとしたボエティウスとイシドールス、そして東ローマ帝国で新しい数学研究を続けたアンテミオスとイシドロスが、それぞれどのような功績を残したのかがわかります。

5世紀から7世紀の数学史年表

この時代の東西ヨーロッパの数学史を、年表で比較してみましょう。

年	西ヨーロッパ	東ヨーロッパ
475年頃		アンテミオス、イシドロス誕生
476年	西ローマ帝国滅亡
480年頃	ボエティウス誕生
500年頃	ボエティウスがユークリッドなどの著作を要約した書籍を執筆する
510年	ボエティウスが執政官に就任
524年	ボエティウスが処刑される
532年		ハギア・ソフィア大聖堂再建開始
532年頃		アンテミオスやイシドロスがアルキメデスの知識を継承し、大聖堂の建設に活用する
534年頃		アンテミオス死去
537年頃		イシロドス死去
537年		ハギア・ソフィア大聖堂完成
560年頃	イシドールス誕生
600年	イシドールスがセビリア大司教に就任
7世紀初頭	イシドールスが百科事典『語源論』を書き、その一部に数学が入門書レベルで書かれた
636年	イシドールス死去、『語源論』完成

西ローマ帝国の終焉と知識の保存

西ローマ帝国の崩壊から「暗黒時代」へ

　476年、西ローマ帝国はゲルマン民族の侵入によって滅亡し、ヨーロッパは大きな混乱期に突入しました。

　帝国の崩壊は、社会の安定と統一性を失わせ、学問を支えていたパトロン制度や教育機関も機能を停止させました。

　そのため、ラテン語しか話せない西ヨーロッパの人々にとって、古代ギリシャの偉大な数学者たちの著作は、閉ざされた書物となってしまったのです 。

　313年のミラノ勅令以降、キリスト教の影響力が強まり、神学は西ローマ帝国崩壊後のヨーロッパの人々の心の拠り所としてさらに重要視されました。

　神学が重視されたこの時代、数学は実用的な目的のみに焦点が当たります。

　例として、キリスト教の最も重要な行事である復活祭（イースター）の日付計算に必要とされました。

　理論的な探求や新しい発見はもはや行われず、西ヨーロッパの数学は長い停滞の時代、すなわち「暗黒時代」へと入っていきました。

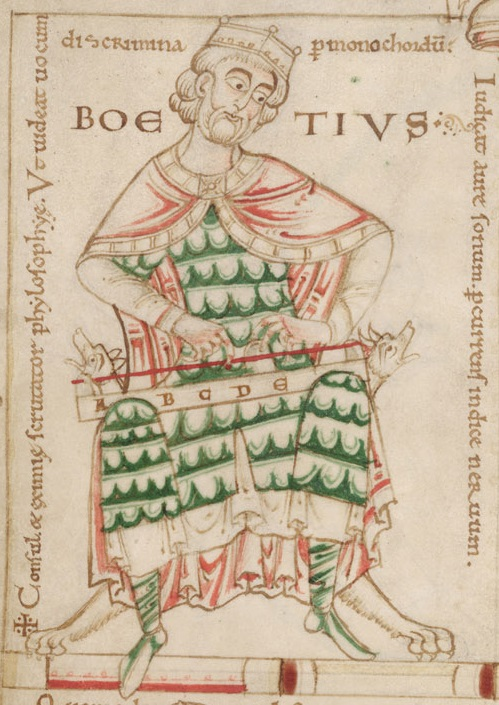
ローマのボエティウスとは

　このような時代の中で、古代の知識をラテン語世界に伝えようと奮闘したのが、アニキウス・マンリウス・セヴェリヌス・ボエティウス（Anicius Manlius Torquatus Severinus Boethius , 480年頃〜524年頃）です。

　彼は「最後のローマ人」とも呼ばれる哲学者・政治家で、東ゴート王国のテオドリック大王に仕えました。

　ボエティウスは、ギリシャの学問が失われることを危惧し、プラトンやアリストテレスの全著作をラテン語に翻訳するという壮大な計画を立てます。

　数学に関しては、以下の教科書を執筆しました。

• 『算術教程』: ニコマコスの『算術入門』の要約。
• 『幾何学』: ユークリッドの『原論』の初歩的な内容の要約。証明はなかった。
• 『天文学』∶プトレマイオスの『アルマゲスト』の引用。

　上記の通り、ボエティウスの著作は、古代の高度な数学を完全に伝えるものではなく、ほとんどが初歩的な要約に留まっていました。

　しかし、これらの教科書は、その後の中世ヨーロッパにおいて、数学教育の基礎を支える標準的なテキストとして、500年以上にわたって修道院学校などで使われ続けることになります。

　ボエティウスの功績は、新しい数学を発見したことではなく、失われゆく古代の知識をかろうじて西ヨーロッパ世界に繋ぎ止めた点にあったのです。

　ボエティウスはその後、政治的または宗教的原因で皇帝の不興を買い、処刑されてしまいました。

セビリアのイシドールスとは

　ボエティウスの死後、西ヨーロッパの学問の状況はさらに悪化します。

　その中で、7世紀に知識の保存に貢献したのが、西ゴート王国（現在のスペイン）のセビリアのイシドールス（Isidore , 560年〜636年）です。

　イシドールスは、当代随一の知識人であり、セビリアの大司教を30年以上務めました。

　彼の主著『語源論（Etymologiae）』は、全20巻からなる百科事典で、そのうちの1巻が算術と幾何学の初歩的な入門書レベルの内容でした。

　イシドールスもまた、ボエティウスと同様に既存の知識を分類・整理し、後世に伝える役割を果たしました。

　『語源論』は、その後何世紀にもわたってヨーロッパ中の修道院で書き写され、中世の知識人にとって最も重要な情報源の一つとなったのです 。

東ローマ帝国での数学の継続と発展

ビザンツ帝国における数学

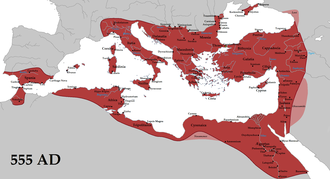
　西ヨーロッパが「暗黒時代」にあった一方で、東ローマ帝国（ビザンツ帝国）では、全く異なる状況が展開していました。

　395年にローマ帝国が東西に分裂した後も、ビザンツ帝国はコンスタンティノープルを首都として存続し、古代ギリシャの言語、文化、学問の伝統を継承していました 。

　西ヨーロッパではギリシャ語が忘れ去られましたが、ビザンツ帝国ではギリシャ語が公用語であり、学者たちはユークリッドやアルキメデス、アポロニウスの著作を直接読むことができました。

　そのため、数学は単なる実用的な計算技術ではなく、学問として生き続けていたのです。

トラレスのアンテミオスとは

　6世紀のビザンツ帝国で活躍したのが、建築家であり数学者でもあったトラレスのアンテミオス（Anthemius , 475年頃〜534年頃）です。

　彼は、ユスティニアヌス帝の命を受け、後述するミレトスのイシドロスと共に、ビザンツ建築の最高傑作であるハギア・ソフィア大聖堂の設計に携わりました 。

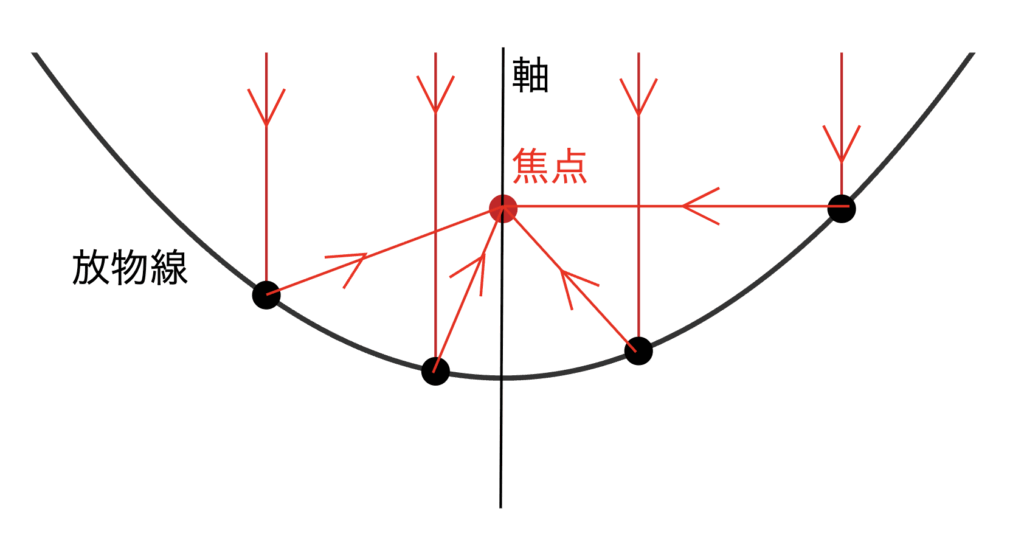
　アンテミオスは放物線の焦点の性質を利用して放物面鏡を設計したり、糸を使って楕円を作図する方法を研究したりするなどの幾何学研究も行いました 。

　レベルとしてはアルキメデスやアポロニウスの研究の再発見に近いですが、西ヨーロッパと異なり、ビザンツ帝国では独創的な数学が多少なりとも継続していたことを示しています。

ミレトスのイシドロスとは

アンテミオスの協力者であったミレトスのイシドロス（475年頃 – 537年頃）もまた、優れた数学者でした。

　数学者としてのイシドロスの功績は、アルキメデスの著作や知識の継承と、幾何学の専門知識を建築学に応用した点にあります。

　建築家としての彼の仕事は、浴場や教会などの設計に及び、ハギア・ソフィア大聖堂の巨大なドーム構造は、アンテミオスとイシドロスの卓越した数学的・工学的知識がなければ実現不可能でした。

　また、T字型の定規と糸で放物線作図する方法を発見したとも言われ、立方体倍積問題を考える一助にもなりました。

　アンテミオスとイシドロスの活動は、ビザンツ帝国において、理論的な数学研究と実践的な応用が見事に結びついていたことを示しています。

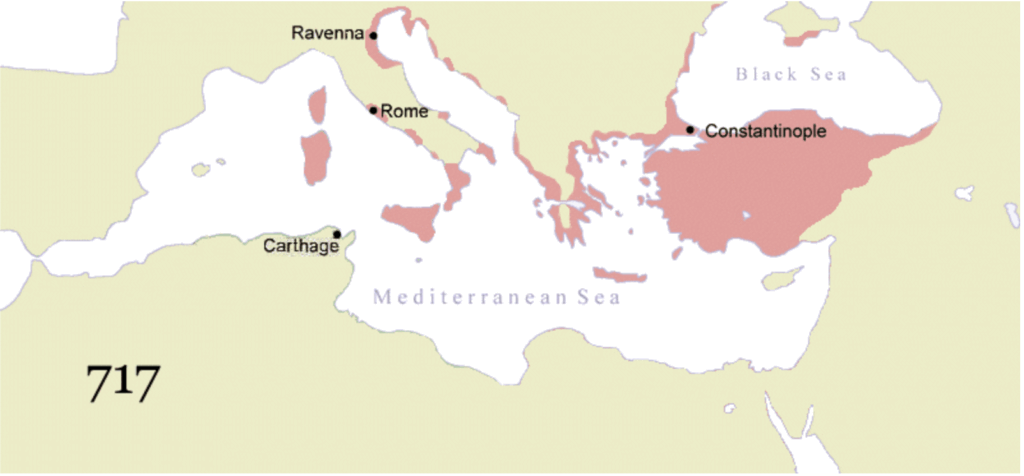
東ローマ帝国も停滞へ

　しかし、ユスティニアヌス帝の時代（6世紀）を頂点として、ビザンツ帝国の数学も徐々に停滞期へと入っていきます。

　7世紀以降、イスラーム帝国の拡大による領土の喪失や、度重なる戦争により、帝国は文化的・経済的に疲弊していきました 。

　西ヨーロッパほどの深刻な「暗黒時代」には陥らなかったものの、アンテミオスやイシドロスに続くような独創的な数学者が現れることは稀になり、学問の中心は古代の著作の注釈や編纂へと移っていきました。

まとめ

5世紀から7世紀にかけて、ヨーロッパの数学は西と東で大きく異なる道を歩みました。

• 西ヨーロッパ世界では、ボエティウスやイシドールスがギリシャ数学の知識をを継承しようと奮闘した
• 東ヨーロッパ世界では、アンテミオスやイシドロスがハギア・ソフィア大聖堂の建築などで数学を応用した
• しかし、東西ヨーロッパ世界の数学はともに衰退の道を歩み、「暗黒時代」へと突入した