現在の数学の源流とも言える古代ギリシャ。
紀元前5世紀から、以下の三大作図問題がギリシャの人々を悩ませていました。
- 円積問題
- 立方体倍積問題
- 角の三等分問題
いずれも定規とコンパスだけを用いた作図に関する問題で、当時解決には至らなかったものの、ギリシャ数学のレベルを押し上げる役割を果たしました。
この記事では、ギリシャの数学者たちが三大作図問題にどう携わり、どのような成果を残したのかを解説。
また、三大作図問題と並んで、当時のギリシャで議論が熱かった3つの他の問題についても触れています!
| 時代 | 紀元前5世紀~紀元前4世紀 |
| 場所 | ギリシャ |
三大作図問題とは?
タレス(Thales , B.C.624頃~B.C.547頃)とピタゴラス(Pythagoras , B.C.569頃~B.C.500頃)により、証明によって数学に厳密性が求められ始めた古代ギリシャ。
紀元前5世紀頃に入り、3つの作図に関する難題が注目を集めていました。
ギリシャで生まれた作図の難問
紀元前5世紀頃から、古代ギリシャの数学者の研究の焦点にあったのが「三大作図問題」(「三大問題」)です。
作図に関する3つの難題をまとめた名称で、それぞれの問題について、以下のような数学者たちが歴史に名を残してます。
| 三大作図問題 | 研究した主な数学者(哲学者) |
| 円積問題 | ・アナクサゴラス(Anaxagoras, B.C.500頃-B.C.428頃) ・ヒポクラテス(Hippocrates,B.C.470頃-B.C.410頃) |
| 立方体倍積問題 | ・ヒポクラテス(Hippocrates,B.C.470頃-B.C.410頃) ・アルキュタス(Archytas, B.C.428頃-B.C.360頃) ・メナイクモス(Menaechmus , B.C.380頃-B.C.320頃) |
| 角の三等分問題 | ・ヒッピアス(Hippias, B.C.460頃) ・パッポス(Pappus , B.C.4世紀頃) |
三大作図問題は、その後約2000年もの間、古今東西の数学を悩ませる難問でした。
古代ギリシャにおいて解決には至らなかったものの、考える過程で様々な数学的成果が生まれ、結果的に三大作図問題はギリシャの数学力を向上させたと言えます。
他に3つの難問の議論も盛んだった
三大作図問題が有名ではあるものの、当時議論が活発であった問題が他に3つありました。
| 三大作図問題 | 研究した主な数学者(哲学者) |
| 無理量問題 | ・ヒッパソス(Hippasus, B.C.5世紀中頃) ・テオドロス(Theodorus,B.C.470頃-B.C.420頃) |
| パラドックス | ・ゼノン(Zeno, B.C.490頃-B.C.430頃) |
| 無限小的方法の妥当性 | ・デモクリトス(Democritos, B.C.460-B.C.379) |
これらの問題については、その後のギリシャ数学の方向性を決める役割を果たしました。
特に、パラドックスや無限小的方法の妥当性により、ギリシャ数学は無限という概念を避けるようになります。
以上の6つの難題について、それぞれの概要と古代ギリシャにおける成果を見てみましょう。
三大作図問題①:円積問題
円積問題は、紀元前1650年頃のエジプトから考えられてきた、世界的にも有名で魅力的な問題です。

概要:円と面積が等しい正方形は作図できるか?
円積問題は、「円の方形化問題」などとも呼ばれる問題です。
1つの円の面積と等しい面積をもつ正方形を作図しなさい。
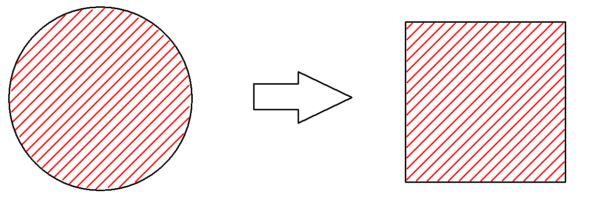
前提として、「作図」=コンパスと定規のみが使える というルールは当時も変わりません。
この問題の最古の研究成果としては、古代エジプトの『リンド・パピルス』の問50に載っている、直径$~d~$の円の面積は$~\displaystyle \frac{64}{81}d^2~$で表されるという知識です。
円の面積が、直径の$~\displaystyle \frac{8}{9}~$を一辺とする正方形の面積と等しいことを主張しています。
成果:ヒポクラテスが月型図形を考えた
ギリシャにおける最古の研究者はアナクサゴラス(Anaxagoras,B.C.500頃-B.C.428)と言われています。

(出典:Eduard Lebiedzki, after a design by Carl Rahl, Public domain, via Wikimedia Commons)
彼は太陽がペロポネソス半島よりも大きい赤熱した石であると主張したがために、牢獄に入れられた人物で、その牢の中で円積問題に取り組みました。
古代ギリシャで、円積問題で一定の成果を上げたのはヒポクラテス(Hippocrates , B.C.470頃-B.C.410頃)です。
月形(図5)から円積問題の解決へと挑みました。
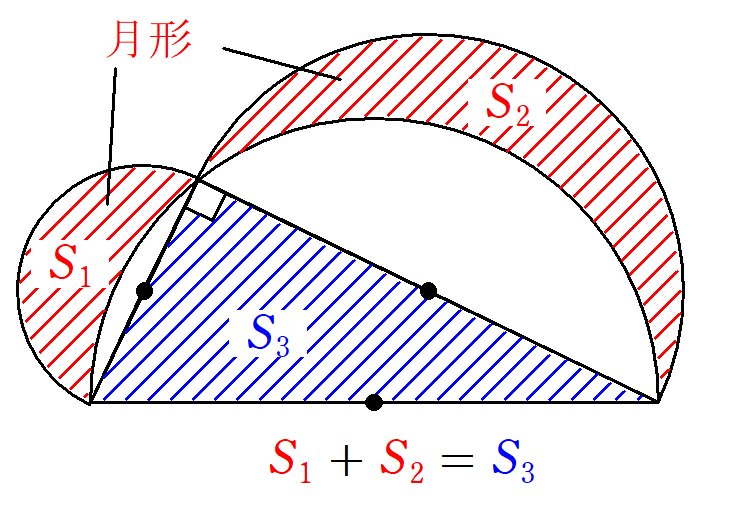
しかし、月形の研究には限界があり、円積問題の部分的な解決に留まりました。
その後も約2000年の間、数学者たちを悩ませてきた円積問題は、1882年にドイツの数学者フェルディナンド・フォン・リンデマン(Ferdinand Von Lindemann, 1852-1939)によって解決されました。

(出典:Unknown authorUnknown author, Public domain, via Wikimedia Commons)
彼は$~\pi~$が超越数であることを証明したため、円積問題は作図不可能と結論づけられたのです。
三大作図問題②:立方体倍積問題
立方体倍積問題は、紀元前5世紀末に神の神託によって登場した問題です。
概要:2の3乗根の作図はできるか?
立方体倍積問題は、立方体の体積を2倍にするための作図方法への挑戦でした。
1つの立方体の$~2~$倍の体積をもつ立方体を作図しなさい。
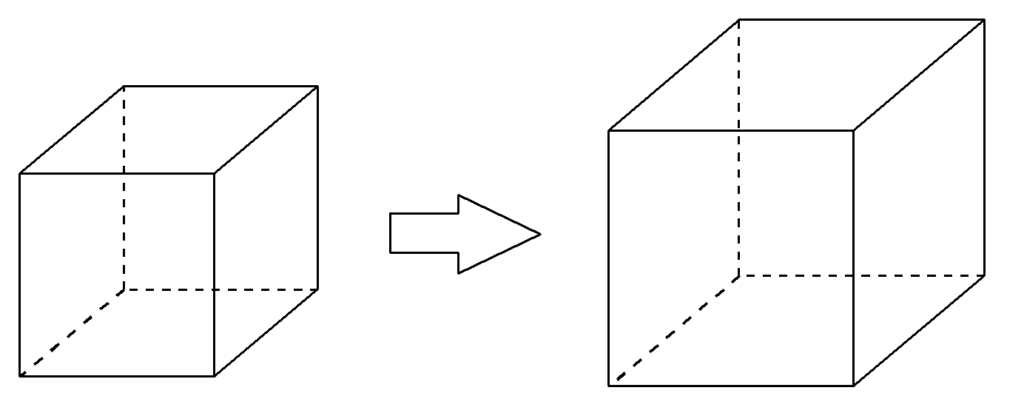
立方体倍積問題は、与えられた一辺の長さを$~\sqrt[3]{2}~$倍することができるかを問うもので、別名「デロス問題」とも呼ばれています。
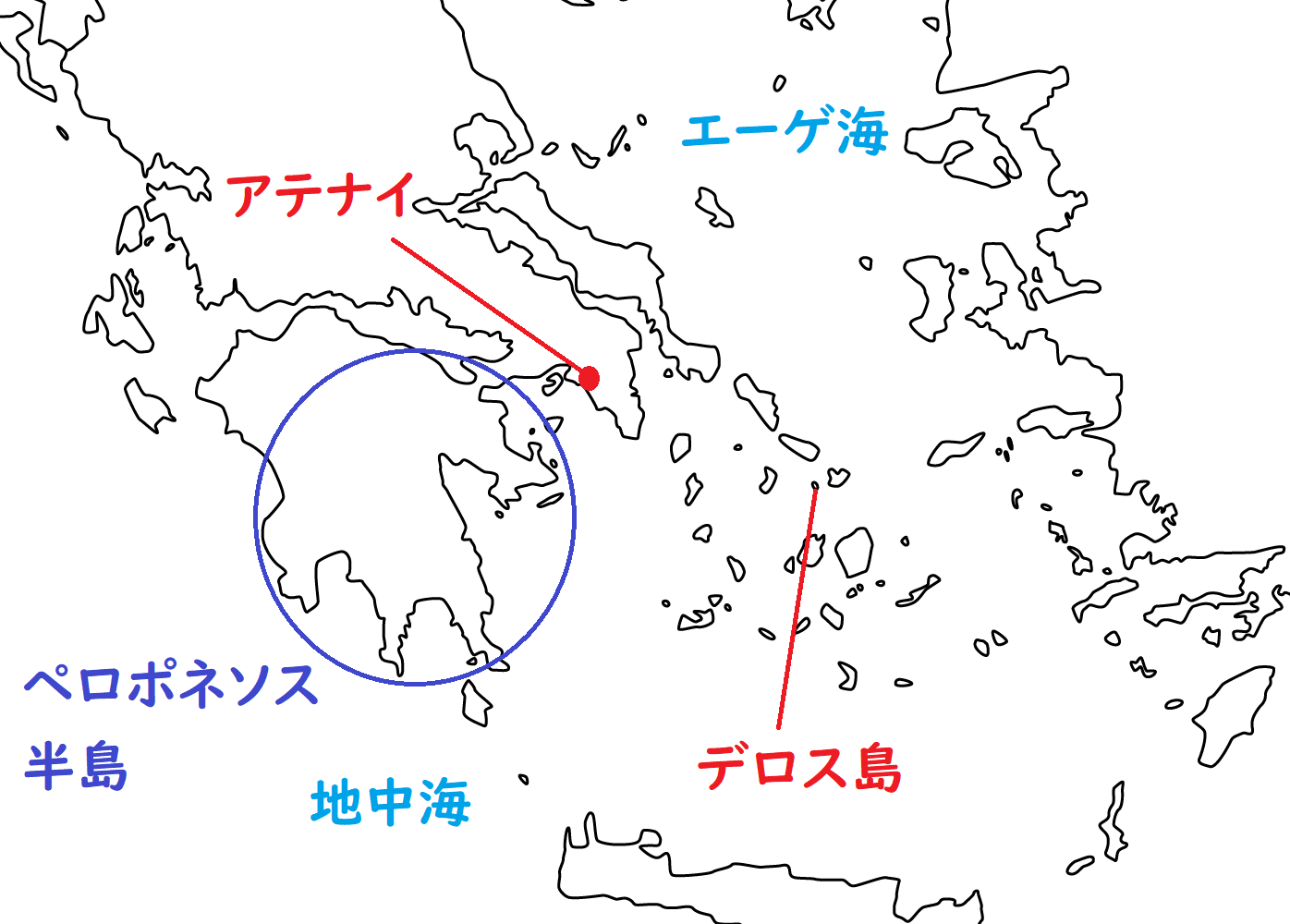
ペロポネソス戦争(アテネとスパルタの戦争。B.C.434年~B.C.404年)末期、アテネでは疫病が流行しました。
アテネはデロス島のアポロン託宣所に代表団を送り、疫病を防ぐための方法を神に伺い立てたところ、
 かみさま
かみさまアポロンの祭壇(立方体の形をしている)の体積を$~2~$倍にせよ。
と神託が下りました。
これが立方体倍積問題の起源であり、「デロス問題」と呼ばれる理由です。

成果:3次元や円錐曲線による作図方法を与えた
立方体倍積問題にまず取り組んだのは、円積問題にも取り組んだヒポクラテスであり、彼は比を使って作図の方針を示したものの、実際に作図をするには至らず断念しました。
次に、アルキュタス(Archytas, B.C.428頃-B.C.360頃)が、2つの円柱を組み合わせた3次元の作図によって解けることを提言しました。
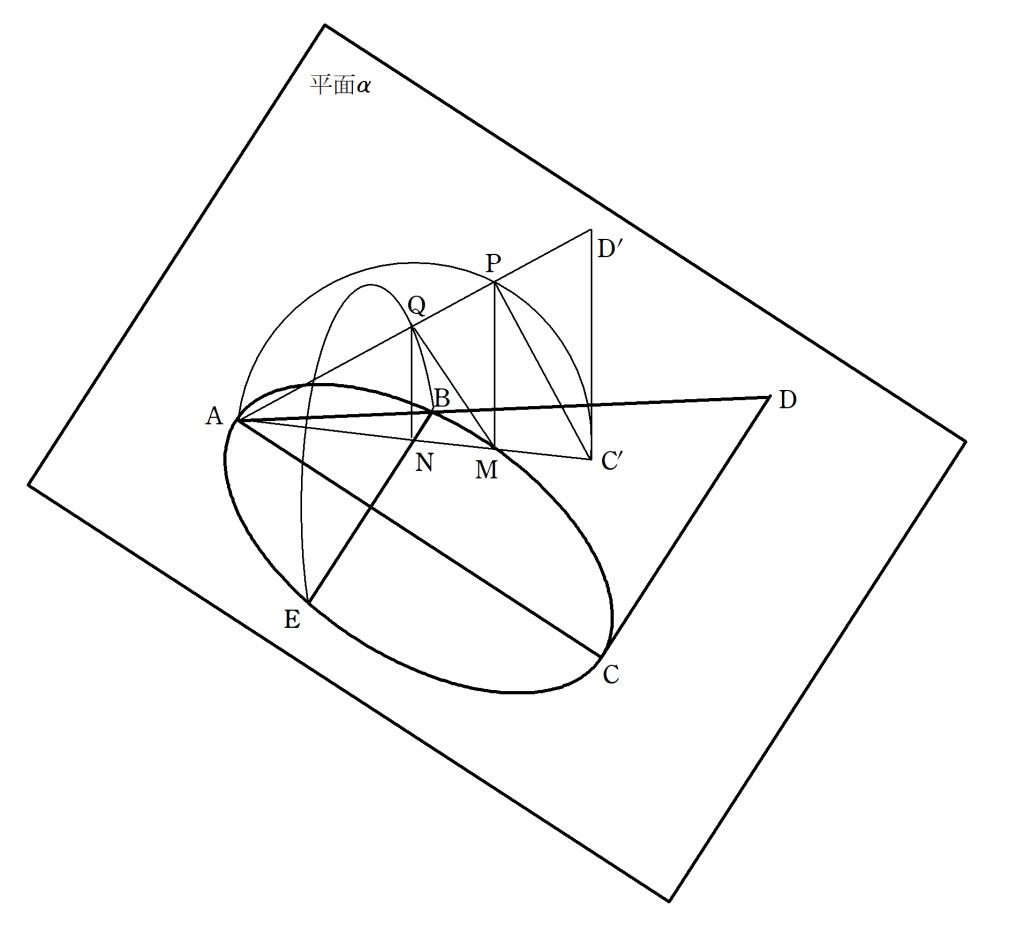

当然ながら、3次元の作図は現実的ではないため、机上の空論に留まりました。
そこから半世紀ほど経ち、同じく古代ギリシャの数学者メナイクモス(Menaechmus, B.C.380頃-B.C.320頃)は、円錐曲線の組み合わせにより、$~\sqrt[3]{2}~$は作図できると提言しました。
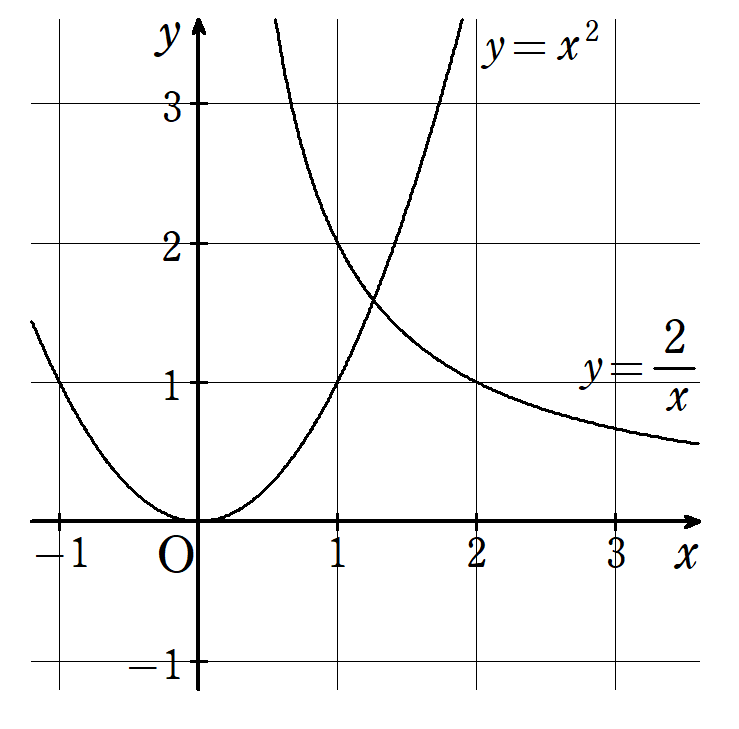

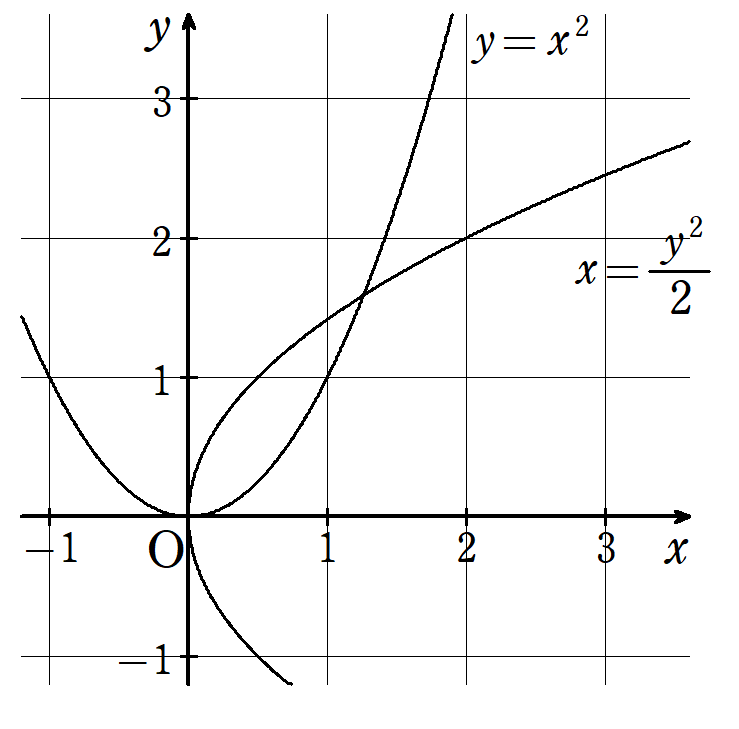

メナイクモスの提言についても、アルキュタス同様、理論的には正しかったものの、円錐曲線の作図ができなかったため、現実的には作図不可でした。
その後も特殊な状況下での作図方法が提案されたものの、定規とコンパスだけを用いた平面での作図方法は登場しませんでした。
問題の誕生から2000年以上経った1837年、ピエール・ワンツェル(Pierre Wantzel, 1813-1848)が$~\sqrt[3]{2}~$は作図不可能であることを証明し、この問題に終止符が打たれました。
三大作図問題③:角の三等分問題
立方体倍積問題が関心の的であった紀元前5世紀末、政治が混乱しているにも関わらず、アテネでは「角の三等分問題」についても注目が集まっていました。
概要:角の三等分線は作図できるか?
角の三等分線問題は、その名の通り、角を三等分するための作図問題です。
1つの角を三等分する直線を作図しなさい。
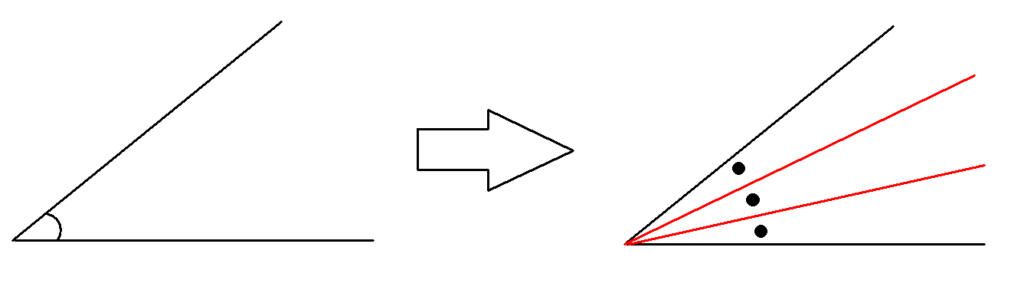

この問題の起源こそ謎ですが、
- $~2~$の平方根の作図ができる → $~2~$の立方根の作図はできる?(立方体倍積問題)
- 角の二等分線の作図ができる → 角の三等分線の作図はできる?(角の三等分問題)
というような流れから来ているのではないかと思います。
成果:ヒッピアスが円積線を利用した
この問題に一定の解を導き出したのは、ヒッピアス(Hippias , B.C.460頃-不明)です。
彼は円積線という特殊な曲線を使うことで、角の三等分ができることを示しました。
しかし、円積線自体の作図が難しく、解決には至りませんでした。
<図13> 円積線のアニメーション
(左のスライダーを動かすと、円積線が赤で描けます)
立方体倍積問題と同様、その後も特殊な曲線を使用した作図方法が生み出されたものの、その特殊な曲線の作図ができなかったため、根本的な解決には至りませんでした。
そして2000年以上経った1837年、立方体倍積問題と同様、ピエール・ヴァンツェルによって角の三等分は作図不可能であることが示されました。
他の難問①:無理量問題
古代ギリシャでは、三大作図問題以外にも盛んに議論された問題がありました。
その中の一つが「無理量問題」(「共測不能問題」「通約不能問題」とも)です。
概要:無理数は存在するか?
無理量は今で言う無理数のことであり、無理量問題とは無理数が存在するかどうかを考える問題です。
最も代表的なのは、$~\sqrt{2}~$に関する問題になります。
$~\sqrt{2}~$は、$~\displaystyle \frac{自然数}{自然数}~$の形で表すことができない。
この問題の歴史は三大作図問題よりも古く、ピタゴラス(Pythagoras , B.C.569頃-B.C.500頃)の時代までさかのぼります。


(出典:The original uploader was Galilea at German Wikipedia., Public domain, via Wikimedia Commons)
「万物は数である」を教義として掲げていたピタゴラス教徒は、どんな数も自然数の比$~ \displaystyle \left( \frac{自然数}{自然数} \right)~$で表されるという考えを持っていました。
そのため、ピタゴラスの定理から導かれる$~\sqrt{2}~$や教団のシンボルマークに出てくる$~\sqrt{5}~$も自然数の比で表すための手段があると信じていたはずです。
成果:√2が無理数であると証明された
しかし、ピタゴラス教徒の1人であるヒッパソス(Hippasus , B.C.5世紀中頃活躍)は、$~\sqrt{2}~$が無理量であることを何らかの方法で示しました。


(出典:Boccanera G., Public domain, via Wikimedia Commons)
さらにテオドロス(Theodorus , B.C.470頃-B.C.420頃)は、$~\sqrt{3}~,~\sqrt{5}~,~\sqrt{7}~,~\sqrt{11}~,~\sqrt{13}~,~\sqrt{17}~$が無理量であることを幾何的に証明しています。
無理量問題については、無理数は存在するという形で議論は終わったものの、ピタゴラス学派の整数信仰を打ち砕く結果に、当時のギリシャに衝撃が走りました。
他の難問②:パラドックス
ギリシャ数学を先導したタレスやピタゴラスは、イオニア地方出身であり、空間と時間はそれぞれ連続する点と瞬間からできていると考え、直感的に点と瞬間を認識していました。
この考え方に異を唱えたのが、エレア派の哲学者たちであり、パラドックスを提起することでイオニア学派に対抗しました。
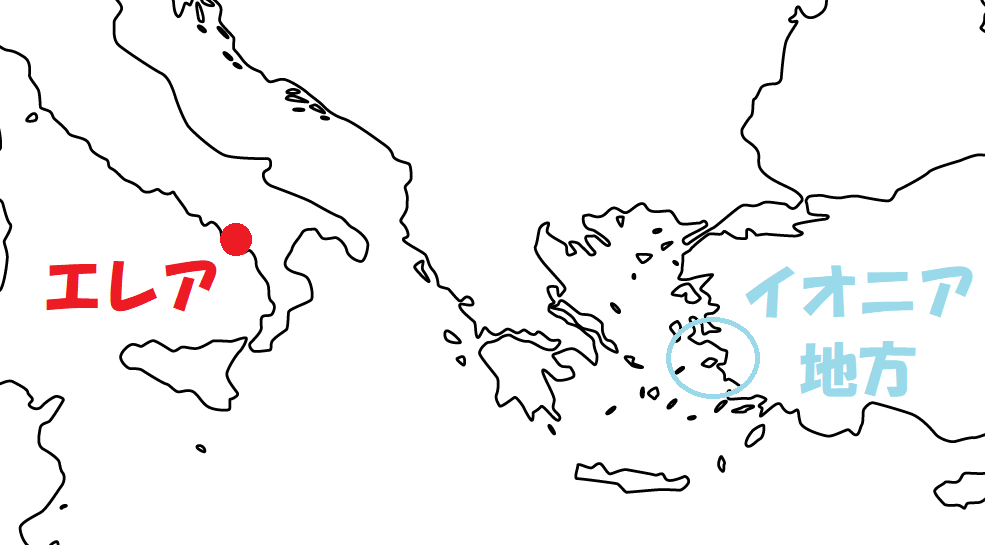

(出典:白地図専門店より改変 / CC-BY-4.0)
概要:正しそうな理論の矛盾を指摘できるか?
エレア派の哲学者たちが提起したパラドックスは、以下のような定義で与えられる問題です。
パラドックスとは、正しくみえる前提や論理から、納得しがたい結論に行きついてしまう問題のことをいう。
エレア派は、イオニア学派の空間と時間に対する考え方では解決できないようなパラドックスを提起することで、自分たちの考え方が正しいことを主張しようとしました。
特にエレア派のゼノン(Zeno, B.C.490頃-B.C.430頃)は、現存するだけでも9個のパラドックスを提示しています。


(出典:ヤン・デ・ビスコップ, CC0, via Wikimedia Commons)
ゼノンが示したパラドックスの中でも有名なのが「アキレスと亀」です。
俊足のアキレスとゆっくり進む亀がいる。
亀がアキレスよりも前方にいるとき、アキレスが進めば亀も進むため、アキレスは亀に追いつくことができない。
アキレスが前を歩く亀に追いつこうとすれば、その間に亀は先に進んでいます。
アキレスがそこから亀に追いつこうとすれば、その間に亀はさらに先に進んでいます。
普通に考えれば足の速いアキレスが亀を追い越すことは容易に思えますが、以上のような考え方をすれば、アキレスは永遠に亀に追いつけないということになります。


成果:大きさを数ではなく線分で表すようになった
パラドックスに関して、イオニア学派とエレア派は議論を重ねてきましたが、イオニア学派はついにパラドックスを解決することができませんでした。
その結果、ピタゴラス学派の時代(紀元前6~5世紀頃)には大きさを小石(calculus)で表していたのに対し、ユークリッド(Euclid , B.C.330頃-B.C.275頃)の時代には大きさを線分で表すようになりました。
ユークリッドの主著『原論』を例に挙げると、$~(a+b)(a-b)+b^2=a^2~$という代数計算をわざわざ幾何的に説明しています。
ある線分を2点によってそれぞれ等しい線分と等しくない線分とに分けたとき、等しくない線分どうしの囲む長方形と2つの区分店の間の線分上の正方形の和は、もとの半分の上の正方形に等しい。
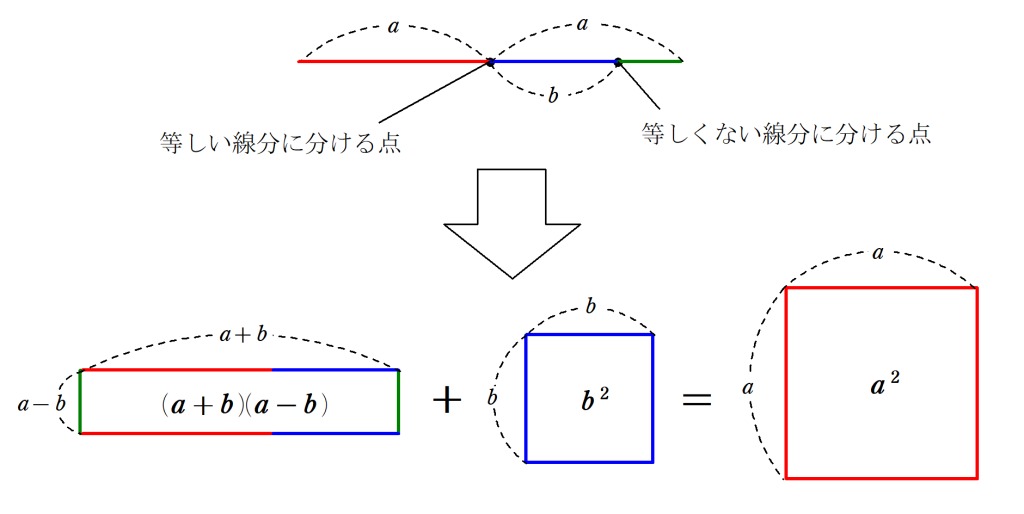

離散的な数ではなく、連続的な線分によって計算することで、パラドックスを回避しようとした姿勢がうかがえます。
実際、数を使ってパラドックスを回避しようとすると、無限級数の収束性が研究される17世紀を待たなければなりませんでした。
他の難問③:無限小的方法の妥当性
パラドックスでも出てきたように、無限を考えることの妥当性は当時のギリシャにとって非常に難解なものでした。
概要:図形を無限個に分割するのは妥当か?
イオニア派で、ゼノンよりも後の時代を生きたデモクリトス(Democritos , B.C.460-B.C.379)は、パラドックスの逆風に悩まされながらも、今で言う「カヴァリエリの原理」を用いて、円錐の体積が円柱の$~\displaystyle \frac{1}{3}~$になる理由を説明しました。


(出典:Unidentified engraver, Public domain, via Wikimedia Commons)
カヴァリエリの原理とは、立体を無限個の平面に切り分けて体積を求める考え方です。
切り口の面積が常に等しい2つの立体の体積は等しい。
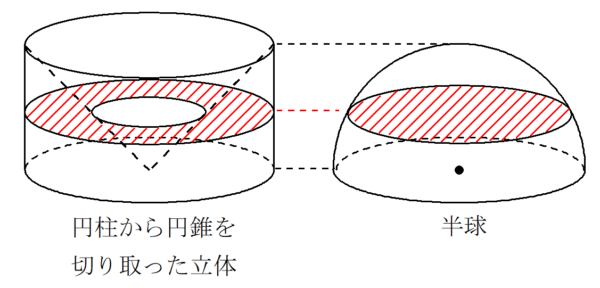

今でこそ認められているカヴァリエリの原理も、当時のギリシャにおいては、立体を無限個に切り分けるのは妥当なのか議論されました。
成果:無限の扱いの難しさを理解
三角柱を体積が等しい3個の三角錐に分割できることを明らかにしたデモクリトスは、カヴァリエリの原理を用いて、円錐の体積も円柱の$~\displaystyle \frac{1}{3}~$であると結論づけました。
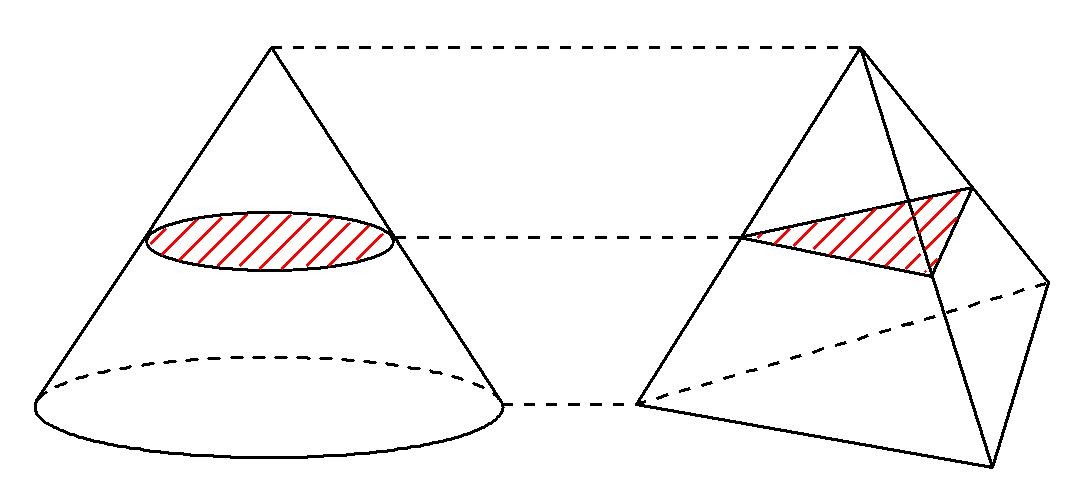

しかし、ゼノンのパラドックスによって、立体を無限個の平面に分けるという考え方は、当時受け入れられませんでした。
感覚的には正しそうでも、エレア派が提唱した無限の妥当性を否定する考え方を論破することができず、それ以降ギリシャでは無限を避けるようになっていきました。
ボナヴェントゥラ・フランチェスコ・カヴァリエリ(1598-1647 , Bonaventura Francesco Cavalieri)の誕生により、デモクリトスの考え方は約2000年越しに認められています。
まとめ
三大作図問題をはじめとする、古代ギリシャで悩まれた6つの問題の概要とその成果について解説してきました。
- 三大作図問題はそもそも厳密な意味での作図ができない問題であるものの、月形図形や円積線などの発明といった副産物があった。
- 古代ギリシャの時代から、無理数の存在は認められた。
- エレア派のパラドックスにより、古代ギリシャでは無限を避けるようになった。
エジプトやバビロニアの実生活に基づいた数学とは異なり、思考の精密さを問う数学が古代ギリシャで流行したことがわかるでしょう。
次の記事からは、6つの問題が取り挙げられている中を生きた数学者たちを、一人ひとり解説していきます。





作図できるかという技術的な問題だけでなく、論理に関する問題も存在しているたのがギリシャらしいね。



ギリシャ人は議論好きだったからね。
それゆえ、数学の発展もエジプトやバビロニアに比べて速かったんだ。
参考文献(本の紹介ページにリンクしています)
- 『カッツ 数学の歴史』,pp.55-118
- 『メルツバッハ&ボイヤー 数学の歴史Ⅰ』,pp.60-79
- 『数学史 数学5000年の歩み』,pp.111-119
- 『数学の歴史物語』,pp.45-63
- 『数学の流れ30講(上)』,pp.28-31
- 『世界数学者事典』
- 『数学者図鑑』, pp.22-23
- 『ずかん 数字』,p66
- ポール・パーソンズ、ゲイル・ディクソン(2021)『図解教養事典 数学』,p.23,NEWTON PRESS
- 吉永良正(2008)『アキレスとカメ』
- T・L・ヒース著,平田寛・菊池俊彦・大沼正則訳(2009)『復刻版 ギリシア数学史』,pp85-157


コメント