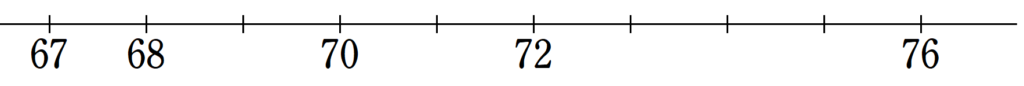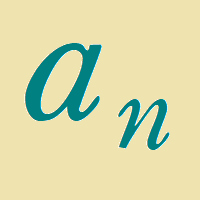未分類– category –
未分類
-

私学適性(数学)平成30年度解説 大問1
東京都私学教員適性検査の過去問(平成30年度)の答えを解説付きで載せています。問題集の解答例で、解法を調べたい際にご活用ください。大問1(本ページ)大問2大... -

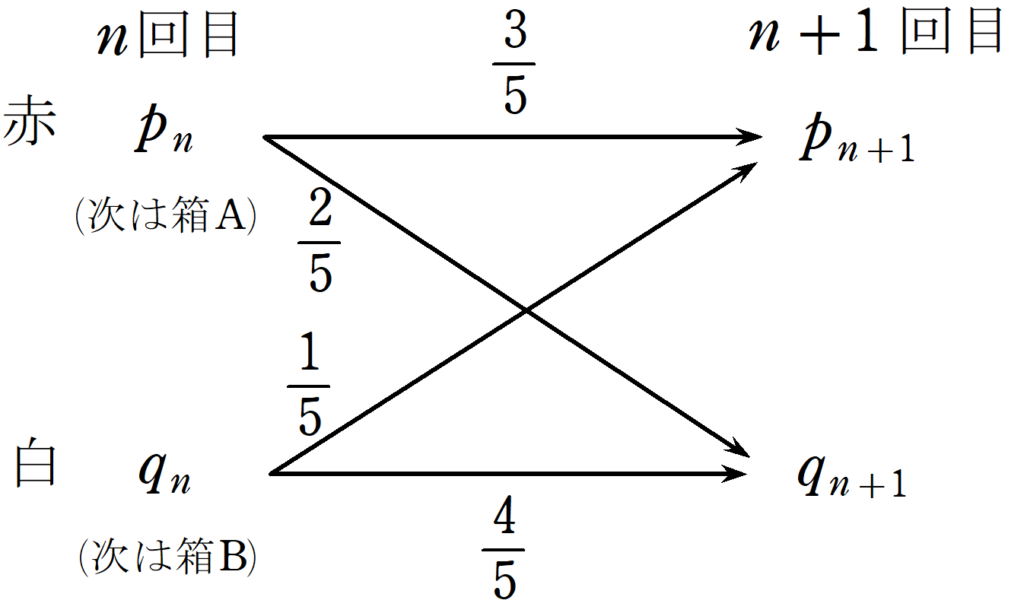
平成29年度実施 私学適性検査数学 全問解説
毎年8月末に行われる私学適性検査。その解説を作成しました。解法の一例として、参考にしてください。 -

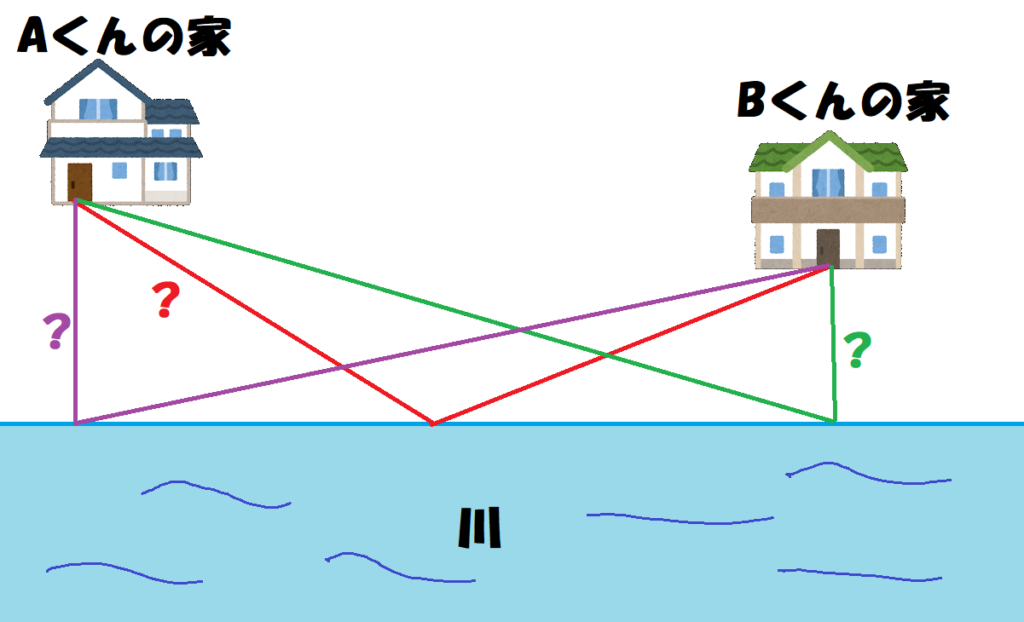
折れ線の最短距離
折れ線の最短距離は、線対称な位置に点をずらし、直線で結ぶことで求まります。 この記事では、なぜその作図方法が最短になるのかを証明します。 Ⅰ 最短距離の作図... -

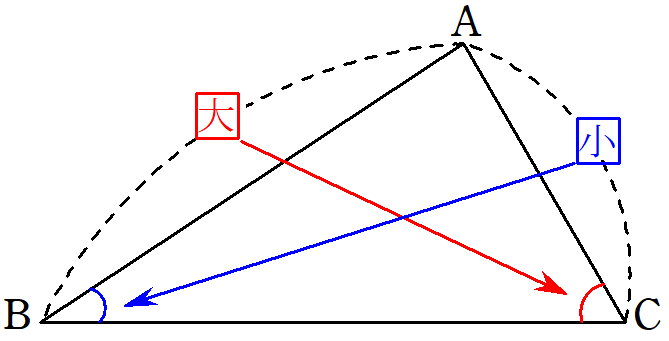
三角形の辺と角の大小~正弦定理でも活用? 証明から使用例まで~
すべての三角形において、辺の長さとそれに対する角の大きさの大小関係には関係があります。当たり前に思えるこの関係について、証明や使用例まで含めて、ていねいに解説します。 -

1/81や1/9801の秘密
小数にすると、興味深い数列が並ぶ $~\displaystyle \frac{1}{81}~$ や $~\displaystyle \frac{1}{9801}~$ 。どのような数列となり、またなぜそのような数列が生まれ... -

3×3魔方陣のすごい性質
3×3魔方陣に関する性質の最終回。あっと驚く性質を紹介します。 Ⅰ すごい性質 Ⅱ 証明 ★魔方陣の関連記事はこちら↓★ ・「3×3の魔方陣の作り方」 ・「3×3魔方陣の... -

3×3魔方陣のもつ性質
今回は3×3魔方陣に隠された面白い性質について紹介します。 Ⅰ 両端平方和の法則 Ⅱ 中央積和の法則 ★魔方陣の関連記事はこちら↓★ ・「3×3の魔方陣の作り方」 ・「... -

3×3の魔方陣の作り方
縦・横・斜めの数の和がすべて等しくなるように数が配置される魔方陣。 この記事では、3×3の魔方陣の論理的な作り方を解説します。 -

ディオファントスの墓
3世紀の数学者ディオファントスが、自身の墓に残した一次方程式の問題です。その解法を2通り紹介します。 -

特性方程式で漸化式が解ける理由
漸化式を解く際に有効な手段として、特性方程式の解を使って式変形をする方法があります。 なぜ特性方程式の解が式変形の上で有効なのかを解説します。