シンプソンの公式は単純な積分のみならず、考え方次第では体積を求めるのにも使えます。
前回に引き続き、その例をいくつか紹介します。
Ⅰ 体積への拡張
Ⅱ 球の体積
Ⅲ 半球の体積
Ⅳ 2円柱の交差部分の体積
Ⅰ 体積への拡張
「シンプソンの公式(応用編①)」にも書きましたが、再掲しておきます。
$~f(x)~$ が3次以下の関数のとき、次の式が成り立つ。
\begin{equation}
\displaystyle \int_{a}^{b} f(x)dx=\frac{(b-a)}{6} \left\{ f(a)+4f\left( \frac{a+b}{2} \right) +f(b) \right\}
\end{equation}
\begin{align}
&\displaystyle \int_{a}^{b} f(x)dx \\
\\
&=\frac{(b-a)}{6} \left\{ f(a)+4f\left( \frac{a+b}{2} \right) +f(b) \right\}
\end{align}
証明や基本例は「シンプソンの公式(基本編)」を参照してください。
前回から考えているのは体積への応用です。高さが $~a~$ から $~b~$ までの範囲で、面積が3次以下の関数で増減するようであれば、シンプソンの公式で体積を求めることができます。
ということで、前回よりも少し複雑な例を挙げていきます。前回同様、説明をわかりやすくするため、次のような文字を使います。
$~xyz~$ 空間で、 $~f(z)~$ は高さ $~z~$ で切った立体の断面積とし、一番高いところを $~z=t~$ 、一番低いところを $~z=s~$ とすると、
求めたい体積は $~\displaystyle \int_{s}^{t}f(z)dz $と表せる。
また、立体の高さの半分の位置を $~\displaystyle \frac{t+s}{2}=m~$ としておく。
よって、シンプソンの公式で体積は次のように計算できる。
\begin{equation}
\displaystyle \frac{t-s}{6} \left\{ f(s)+ 4f(m) +f(t) \right\}
\end{equation}
では、シンプソンの公式の応用例の後半戦を見ていきましょう。
Ⅱ 球の体積
半径 $~r~$ の球の体積
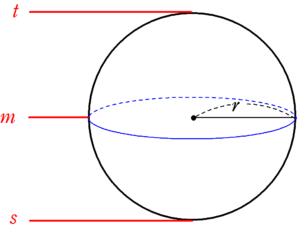
情報を整理する。
\begin{align}
\displaystyle f(t)&=0 \\
f(s)&=0 \\
\\
f(m)&=\pi r^2 \\
\\
t-s&=2r
\end{align}
次に面積の増減を考える。
原点を中心とした場合、球の方程式は
\begin{equation}
x^2+y^2+z^2=r^2
\end{equation}
であるため、式変形をすると、
\begin{equation}
x^2+y^2=r^2-z^2
\end{equation}
となるので、高さ $~z~$ における断面は半径 $~\sqrt{r^2-z^2}~$ の円とわかる。
よって、高さ $~z~$ に対する断面積は $~\pi (r^2-z^2)~$ で、 $~z~$ の二次関数となる。
以上より、体積は
\begin{align}
&\displaystyle \frac{t-s}{6} \left\{ f(s)+ 4f(m) +f(t) \right\} \\
\\
&=\frac{2r}{6} \left\{ 0+ 4 \pi r^2 + 0 \right\} \\
\\
&=\frac{r}{3} \cdot 4 \pi r^2 \\
\\
&=\frac{4}{3}\pi r^3
\end{align}
これで求まりました「身の上に心配があるので参上」
Ⅲ 半球の体積
半径 $~r~$ の半球の体積
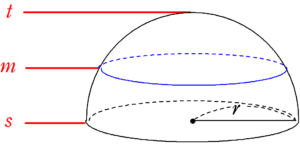
情報を整理する。
\begin{align}
\displaystyle f(t)&=0 \\
f(s)&=r^2 \\
\\
t-s&=r
\end{align}
次に $~z=m~$ のときの断面の円の半径を考える。底面の円の中心を通る面で切断すると、下のような図になる。
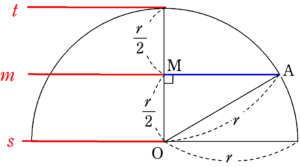
$~\triangle OMA~$ で、 $~OM=\displaystyle \frac{r}{2}~$ 、 $~OA=r~$ より、 $~OM:OA=1:2~$ 。
$~\triangle OMA~$ は $~\angle MOA=60°~$ の直角三角形であることがわかる。
したがって、 $~z=m~$ のときの断面の円の半径は $~MA=\displaystyle \frac{\sqrt{3}r}{2}~$ とわかる。
よって、
\begin{align}
f(m)&=\displaystyle \pi \left( \frac{\sqrt{3}r}{2} \right)^2 \\
\\
&=\frac{3\pi r^2}{4}
\end{align}
となる。
また、 $~z~$ に対する面積の増減は、上の応用例4と同様 $~z~$ の二次関数となる。
以上より、体積は
\begin{align}
&\displaystyle \frac{t-s}{6} \left\{ f(s)+ 4f(m) +f(t) \right\} \\
\\
&=\frac{r}{6} \left\{ 0+ 4 \cdot \frac{3\pi r^2}{4}+ \pi r^2 \right\} \\
\\
&=\frac{r}{6} \cdot 4 \pi r^2 \\
\\
&=\frac{2}{3}\pi r^3
\end{align}
確かに球の体積の半分になっています。
Ⅳ 2円柱の交差部分の体積
最後は少し考えにくい直交する2円柱の交わった部分の体積を求めます。
側面がそれぞれ $~x^2+z^2=r^2,y^2+z^2=r^2~$ で表される2円柱の共有部分の体積
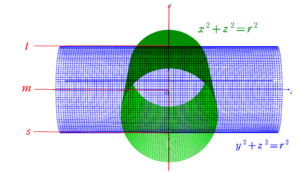
情報を整理する。
\begin{align}
\displaystyle f(t)&=0 \\
f(s)&=0 \\
\\
t-s&=2r
\end{align}
次に面積の増減を考える。
高さ $~z~$ を固定して考えると、それぞれの円柱の側面は次のように切り取られる。
\begin{align}
x^2+z^2&=r^2 \\
x^2&=r^2-z^2 \\
x&=\pm \sqrt{r^2-z^2} \\
\end{align}
同様に
\begin{equation}
y= \sqrt{r^2-z^2}
\end{equation}
これらを高さ $~z~$ における $~xy~$ 平面で表すと、次のようなグラフとなる。
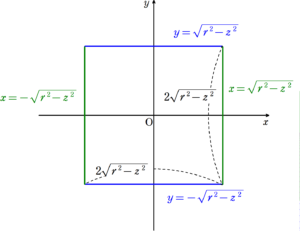
高さ $~z~$ における断面積は
\begin{align}
(2\sqrt{r^2-z^2})^2 &=4(r^2-z^2)
\end{align}
となり、 $~z~$ の二次関数であることがわかった。
また、 $~f(m)~$ は $~z=0~$ のときの断面積なので、
\begin{align}
f(m)&=4(r^2-0^2) \\
&=4r^2
\end{align}
となる。
以上より、体積は
\begin{align}
&\displaystyle \frac{t-s}{6} \left\{ f(s)+ 4f(m) +f(t) \right\} \\
\\
&=\frac{2r}{6} \left\{ 0+ 4 \cdot 4r^2 + 0 \right\} \\
\\
&=\frac{r}{3} \cdot 16r^2 \\
\\
&=\frac{16}{3}\pi r^3
\end{align}
もちろん、 $~\displaystyle \int_{-r}^{r} 4(r^2-z^2)dz~$ を計算しても同じ答えが出ます。
面積の増減が3次以下の関数でないと、シンプソンの公式が使えないので、その確認を忘れないようにしたいですね。

コメント
コメント一覧 (8件)
先生、いつも本当にありがとうございます!
先生の生徒さんが羨ましいです(T_T)
先生、こんばんは!!
わかりやすい解説シートを書いてくださり、本当にありがとうございます! とてもイメージが深まりました(^^)
先生、もしよろしければチェビシェフの多項式について記事にして頂けませんでしょうか・・
いろいろググっても複雑なことしか書かれておらず・・・><
どんなものか大学入試で必要な視点が学べたらうれしいです!
https://ameblo.jp/ubqubq/entry-10231065147.html
よろしくお願いいたします!いつも本当にありがとうございます!!
イェンゼンの時と同様、調べてみて理解した後、興味あれば記事にしたいと思います。
いつも話題の提供ありがとうございます。
ただ、自分は基本中学生を相手に仕事をしているため、大学入試で必要な視点はわかりかねますm(_ _)m
先生、おはようございます!
今回の記事もものすごく面白かったです^_^
いつもありがとうございます!!
先生! 円に内接する三角形の面積の最大値を求める際、イェンゼンの不等式を用いて考えるエレガントな解法があるようですが、イェンセンはググっても数式ばかりで、実際には答案にどのように使えばいいのか、どういう場合に使えばいいのかがわかりません><
もし取り上げていただけましたらうれしいです^_^
いつもありがとうございます!
いつもご覧いただきありがとうございます。
イェンゼンの不等式、勉強不足で初めて知りました。
勉強してみて、面白そうであれば、シンプソンの公式同様記事にしてみたいと思います!
ご返信ありがとうございます^_^
もともとは、半径1の円に外接する三角形で面積最小なものは、正三角形であることを証明せよ、という問題を考えていた時に知りました!
この問題、先生はどのようにアプローチなさりますでしょうか・・
知恵袋にございました、こちらの解説は何を言っているのかわかりませんでした(>_<)
(特に最初の4〜5行の⇆で繋がれているところ)
https://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q1164102566
アドバイスをいただけますと幸いです!
知恵袋の解説については、考えてみたもののよくわかりませんでした・・・m(_ _)m
なんとな~く感覚的には合っているような気もしますが・・・
遅くなりましたが、イェンゼンの不等式による解法ができました。
scanミスで、pdfファイルが3つになってしまいました。お手数ですが、それぞれご覧ください。
イェンゼンの不等式の応用例 (1ページ)
イェンゼンの不等式の応用例 (2ページ)
イェンゼンの不等式の応用例 (3ページ)
参考文献として、
・「Jensen 不等式を活用した解法」,<http://izumi-math.jp/M_Matumoto/Jensen_ver01.pdf >pp.7 , 2018年8月14日アクセス
を参照しています。