虚数 $~i~$ の $~i~$ 乗はなんと実数になります。実際に $~i^i~$ を計算し、近似値を算出しました。
Ⅰ $~i^i~$ の計算
Ⅱ $~i^i~$ の近似値
Ⅰ $~i^i~$ の計算
次の式が成り立つ。
\begin{equation}
\displaystyle i^i=e^{-\left( \frac{\pi}{2}+2n\pi \right)}(n \in \mathbb{Z})
\end{equation}
ただし、主値を考えると、
\begin{equation}
\displaystyle i^i=e^{-\frac{\pi}{2}}
\end{equation}
である。
この式の右辺は虚数 $~i~$ を含んでいないため、実数となります。無理数の無理数乗が必ず無理数にならないことに似ていますね。
では、この計算結果がどう生まれたのかを見ていきましょう。
$~i~$ 乗の部分がわかりにくいので、それを避けるために対数を使います。そのため、使う知識は複素数の対数関数です。
$~x=i^i~$ とする。この式の両辺の自然対数をとって、式変形をしていくと
\begin{align}
\log{x}&=\log{i^i} \\
&=i \log{i} \\
&=i(\log{|i|}+i\arg{i}) \\
\displaystyle &=i \left\{ \log{1}+i \left(\frac{\pi}{2}+2n\pi \right) \right\} (n\in \mathbb{Z}) \\
&=i \left\{i \left(\frac{\pi}{2}+2n\pi \right) \right\} \\
&=-\left(\frac{\pi}{2}+2n\pi \right)
\end{align}
となる。よって、
\begin{equation}
x=i^i=e^{-\left(\frac{\pi}{2}+2n\pi \right)}(n\in \mathbb{Z})
\end{equation}
が成り立つ。
また、主値は上の式で $~n=0~$ のときなので、
\begin{equation}
\displaystyle i^i=e^{-\frac{\pi}{2}}
\end{equation}
とわかる。 $~\blacksquare$
複素数の対数関数の定義にあてはめることで、求めたい式が求まりました。
Ⅱ $~i^i~$ の近似値
Ⅰで、 $~\displaystyle i^i=e^{-\frac{\pi}{2}}~$ が求められました。右辺の実数は、一体どのくらいの数値なのでしょうか。近似値を下のマクローリン展開とエクセルを使って、求めてみました。
$e^x~$ をマクローリン展開すると、次のような式になる。
\begin{equation}
\displaystyle e^x=1+\frac{x}{1!}+\frac{x^2}{2!}+\frac{x^3}{3!}+\cdots \cdots
\end{equation}
ということは、 $~\displaystyle x=-\frac{\pi}{2}~$ を代入して計算することで、近似値が求められます。
ということで、この先はエクセルで計算してみました。
使った計算式はこんな感じ↓
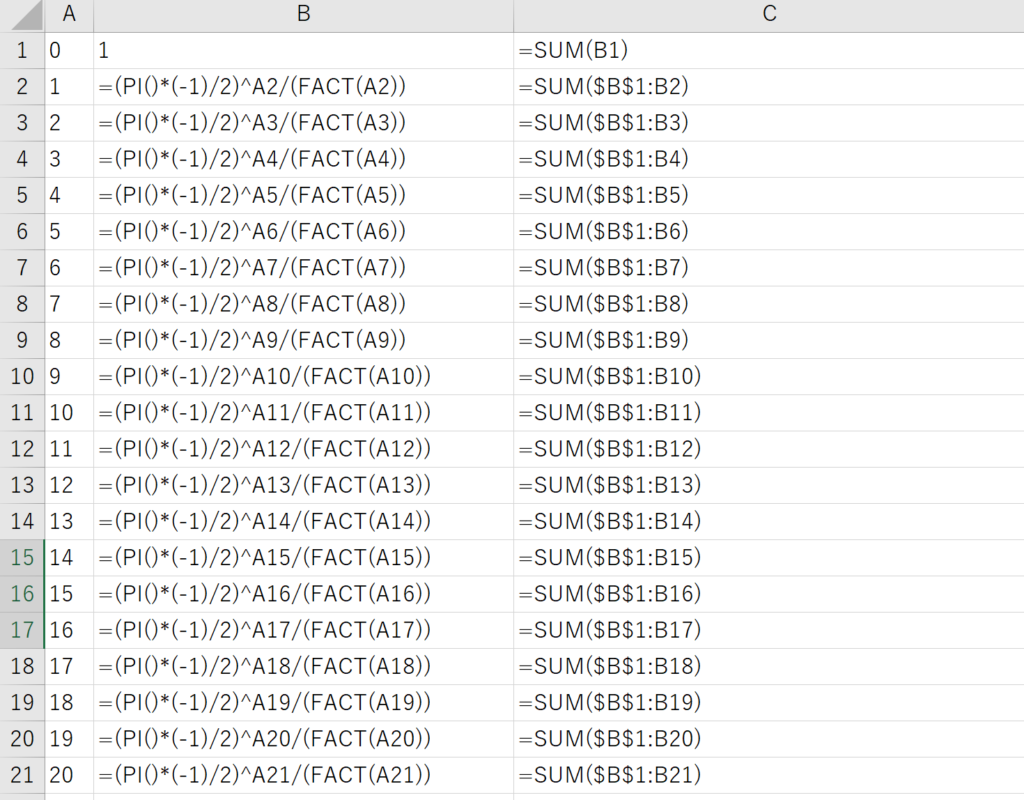
B列に各項の数値、C列にその項までの和が算出されるような関数です。
これによって、計算を行うと、下のように出力されます。
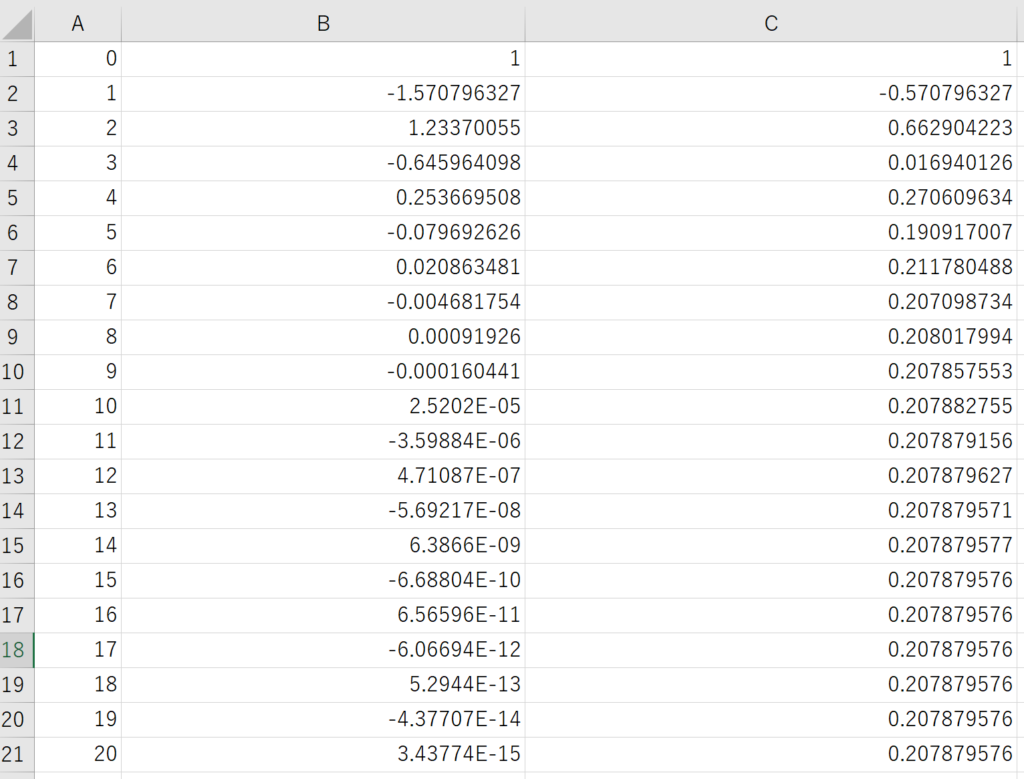
収束速度は割と速く、近似値として、
\begin{equation}
i^i \fallingdotseq 0.207879576 \cdots
\end{equation}
が与えられました!!
短い式の中に、 $~i~$ をはじめ、 $~\pi,e~$ といった数学を代表する記号が使われているのが、オイラーの公式 $~e^{i \pi}=-1~$ を彷彿させますね~。 $~i^i~$ の主値は約0.2。誰かに知識自慢してみましょう。

コメント