空間図形– tag –
-

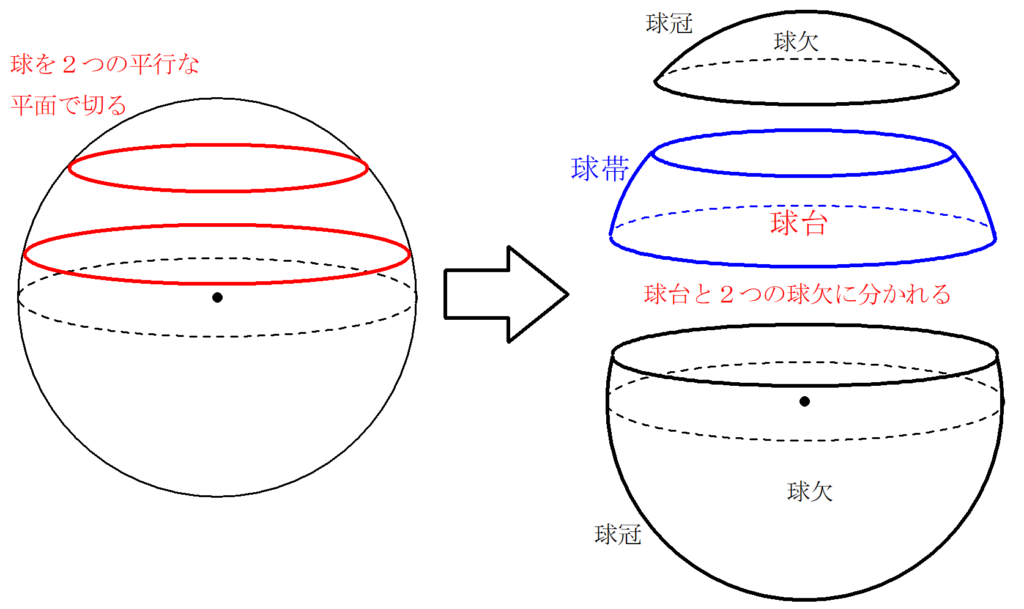
球台と球帯
球を2つの平面で切り取ってできた球台について考えます。 Ⅰ 球台と球帯とは? Ⅱ 球台の体積 Ⅲ 球帯の面積 【Ⅰ 球台と球帯とは?】 前記事の「球欠と球冠」同様... -

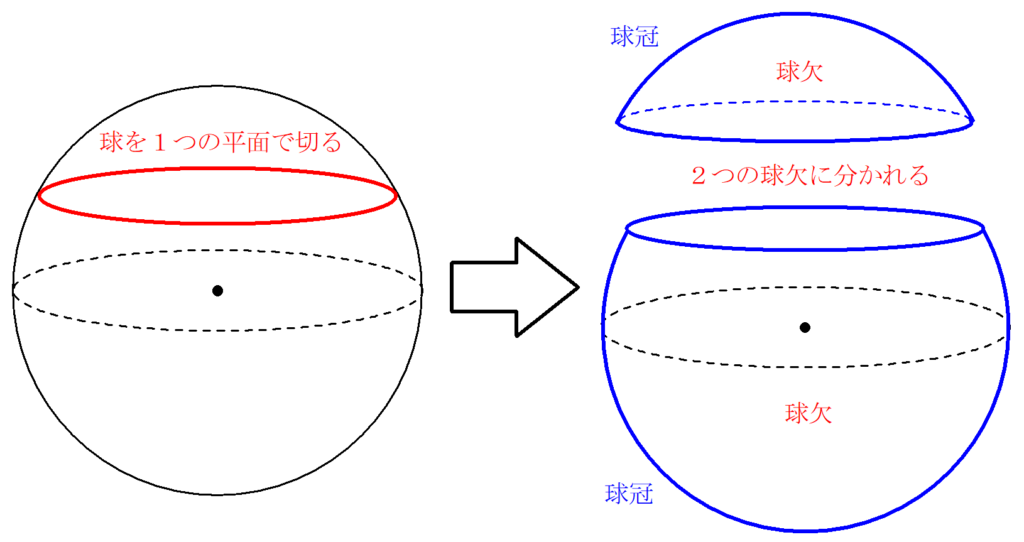
球欠と球冠
球を1つの平面で切り取ってできる球欠という立体について解説します。球欠の体積は、もとの球の半径に依存しない点が面白いです。 -

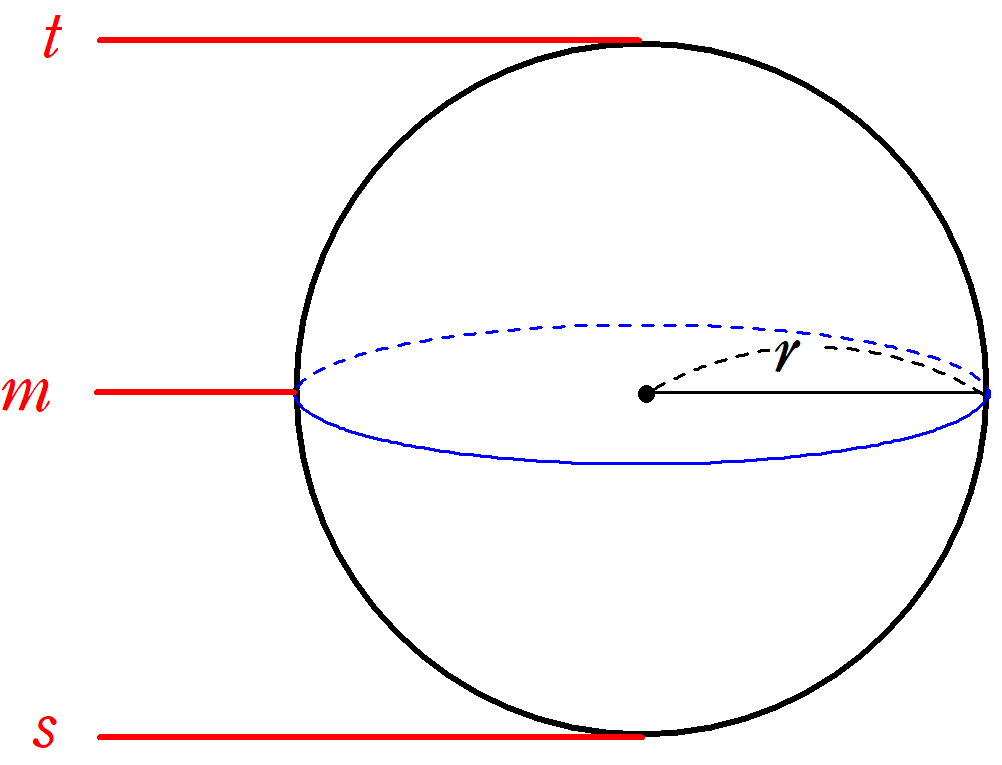
シンプソンの公式(応用編②)
シンプソンの公式は単純な積分のみならず、考え方次第では体積を求めるのにも使えます。 前回に引き続き、その例をいくつか紹介します。 Ⅰ 体積への拡張 Ⅱ 球の体積 Ⅲ... -

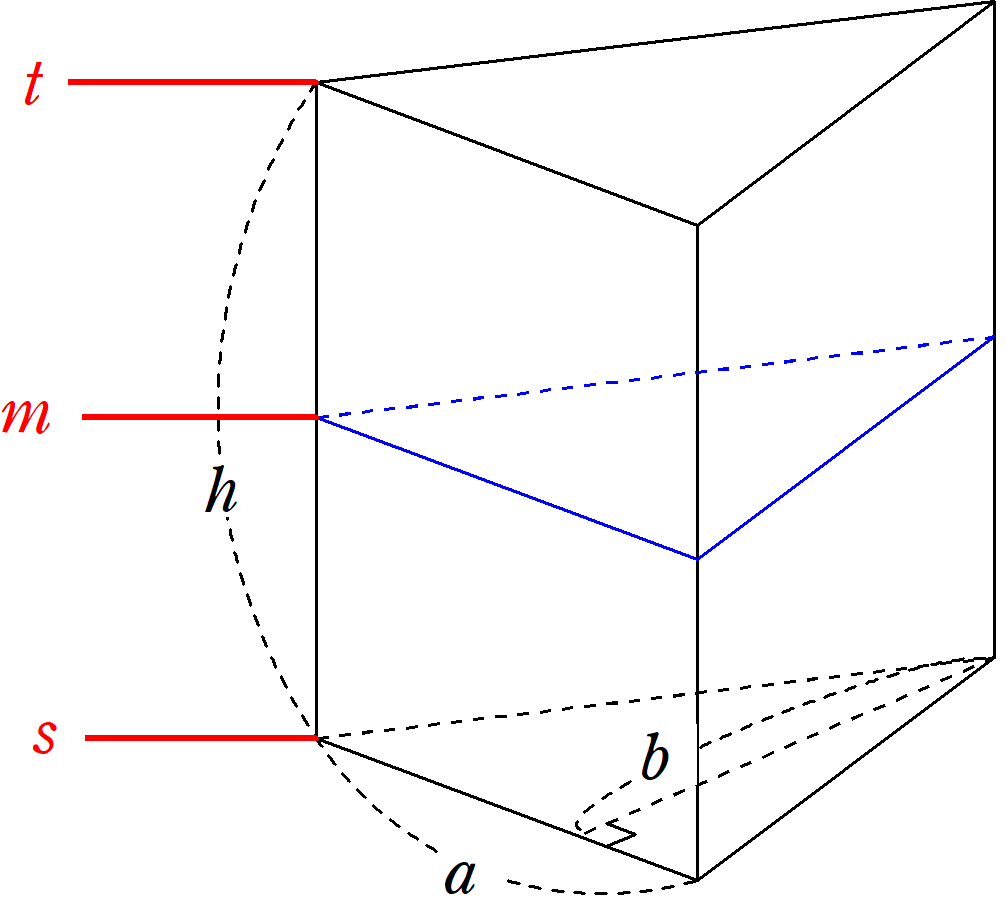
シンプソンの公式(応用編①)
シンプソンの公式は単純な積分のみならず、考え方次第では体積を求めるのにも使えます。 今回はその例をいくつか紹介します。 Ⅰ 体積への拡張 Ⅱ 三角柱の体積 Ⅲ 円錐...
1