微分・積分– tag –

エウドクソスは古代ギリシャの数学者であり、取り尽くし法と比例論で知られています。取り尽くし法は積分の原型と見なされ、比例論では無理数を数学的理解に導入しました。無限小や実数の概念を形成する上での基盤となった彼のこれらの業績を、この記事では解説しています。

　解析学で非常に重要な「テイラー級数」。その基になっているのが「テイラーの定理」です。剰余項を含め、定理の内容を具体例からわかりやすく解説し、証明へと進みます。

　数学Ⅲで、「平均値の定理」を学びますが、本記事の「コーシーの平均値の定理」は、その一般化ともいえる定理となっています。それを例を交えて解説・証明していきます...

数学Ⅲで登場する平均値の定理。微分が絡み、登場する文字数が多いため、数式だけではなかなか理解しづらいのではないでしょうか。この記事では、平均値の定理の意味を例示でわかりやすく説明したうえで、ロルの定理を使って証明します。

3次以下の関数であればシンプソンの公式が成り立ちます。この記事では、なぜ3次以下でないといけないのかを解明していきます。 Ⅰ　シンプソンの公式の誤差 Ⅱ　証明 Ⅰ　...

シンプソンの公式の右辺で、 $~f(a)~$ と $~\displaystyle f\left( \frac{a+b}{2} \right)~$ と $~f(b)~$ の係数が $~1,4,1~$ になる理由を解明していきます。 Ⅰ　シン...

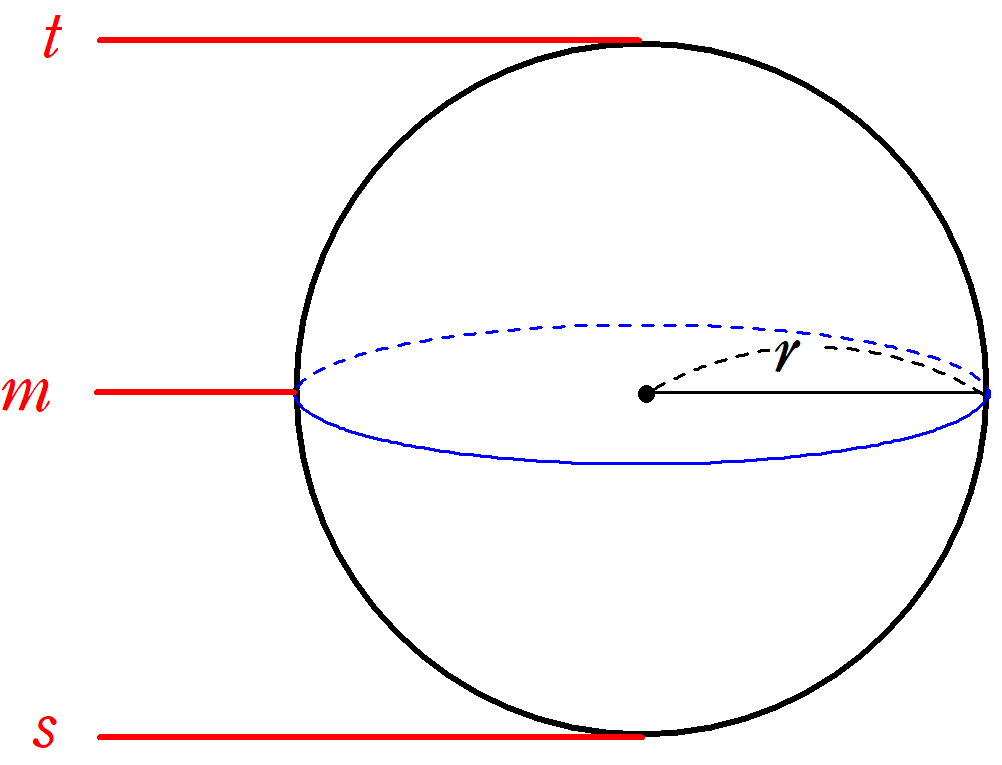
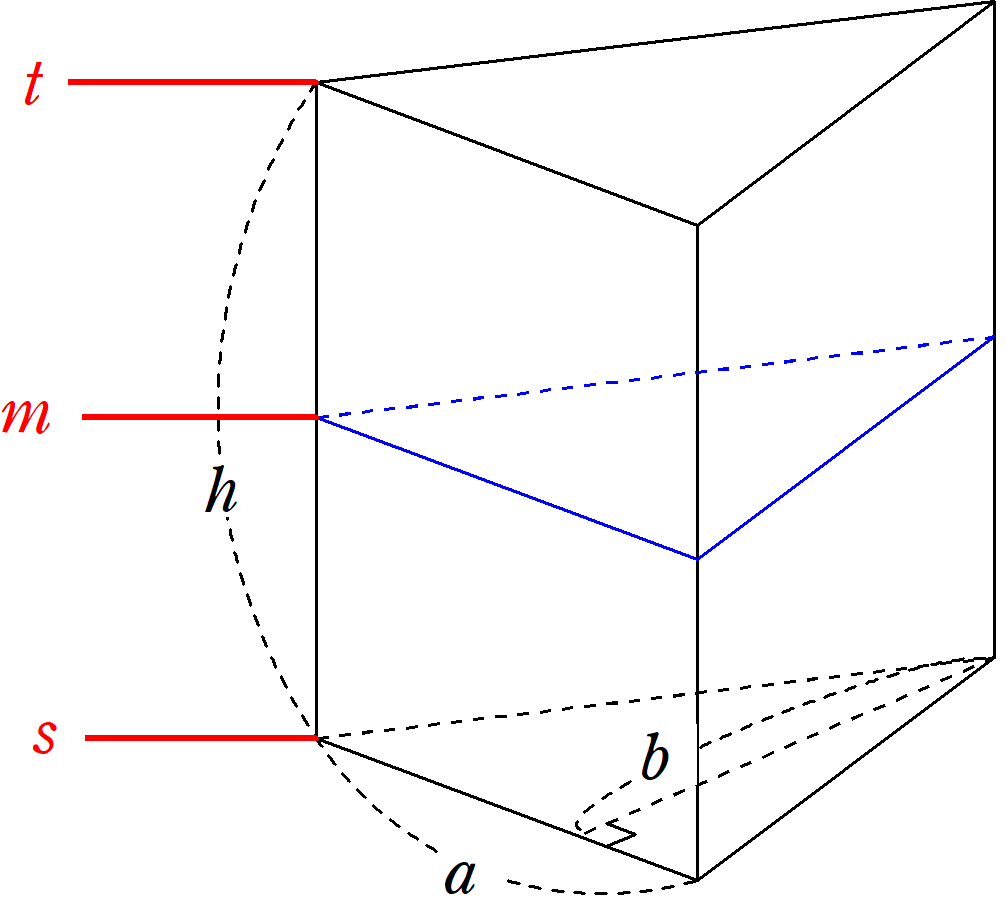
シンプソンの公式は単純な積分のみならず、考え方次第では体積を求めるのにも使えます。 前回に引き続き、その例をいくつか紹介します。 Ⅰ　体積への拡張 Ⅱ　球の体積 Ⅲ...

シンプソンの公式は単純な積分のみならず、考え方次第では体積を求めるのにも使えます。 今回はその例をいくつか紹介します。 Ⅰ　体積への拡張 Ⅱ　三角柱の体積 Ⅲ　円錐...

３次以下の関数の積分を求める際に使えるシンプソンの公式。まずは例と簡単な証明を与えます。Ⅰ　シンプソンの公式Ⅱ　基本例Ⅲ　反例Ⅳ　証明１ Ⅰ　シンプソンの公式 　17...

平均値の定理を証明する上で必要なロルの定理。数学の定理ではよくあることですが、書いてあることは当たり前のことでも、数式にするとわかりづらい内容となっています。この記事では、ロルの定理の意味を例示で説明するとともに、ロルの定理の証明を解説！ロルの定理が使えないパターンも示してあるため、定理の中身をしっかりと理解できます。